初中数学人教版九年级上册23.1 图形的旋转课后练习题

这是一份初中数学人教版九年级上册23.1 图形的旋转课后练习题，共29页。试卷主要包含了旋转的定义，1图形的旋转【素养基础达标】等内容，欢迎下载使用。
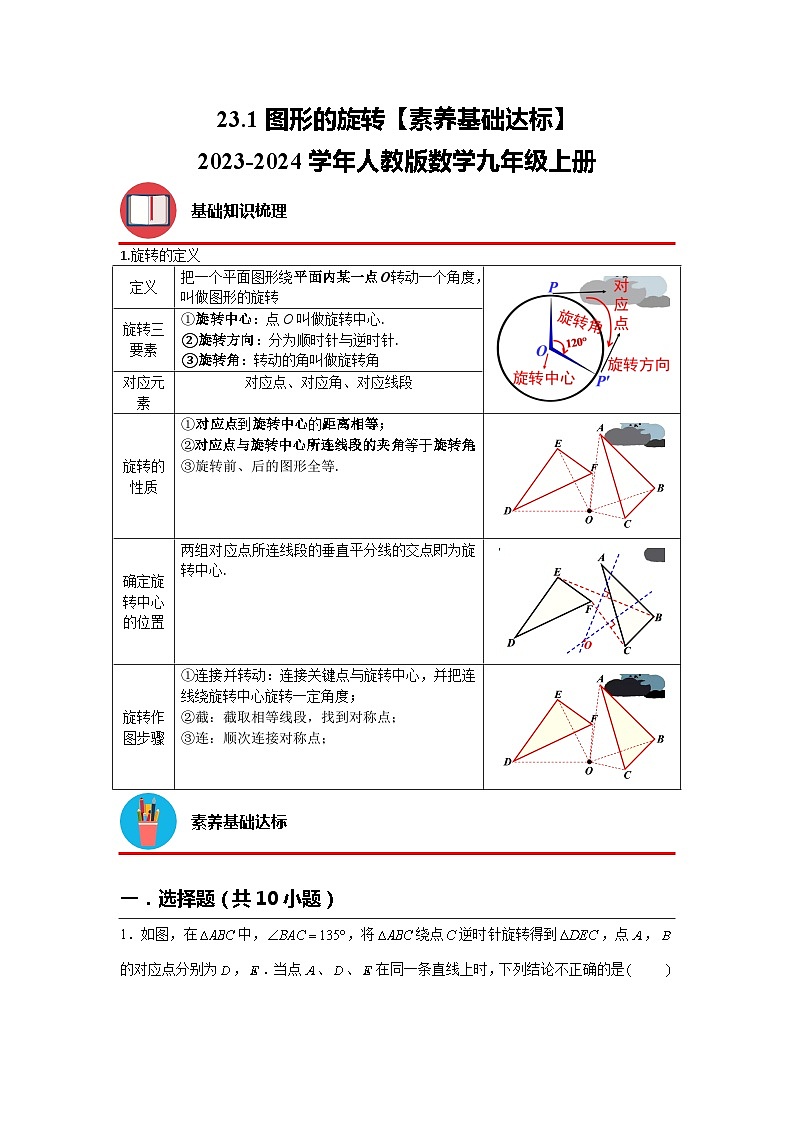
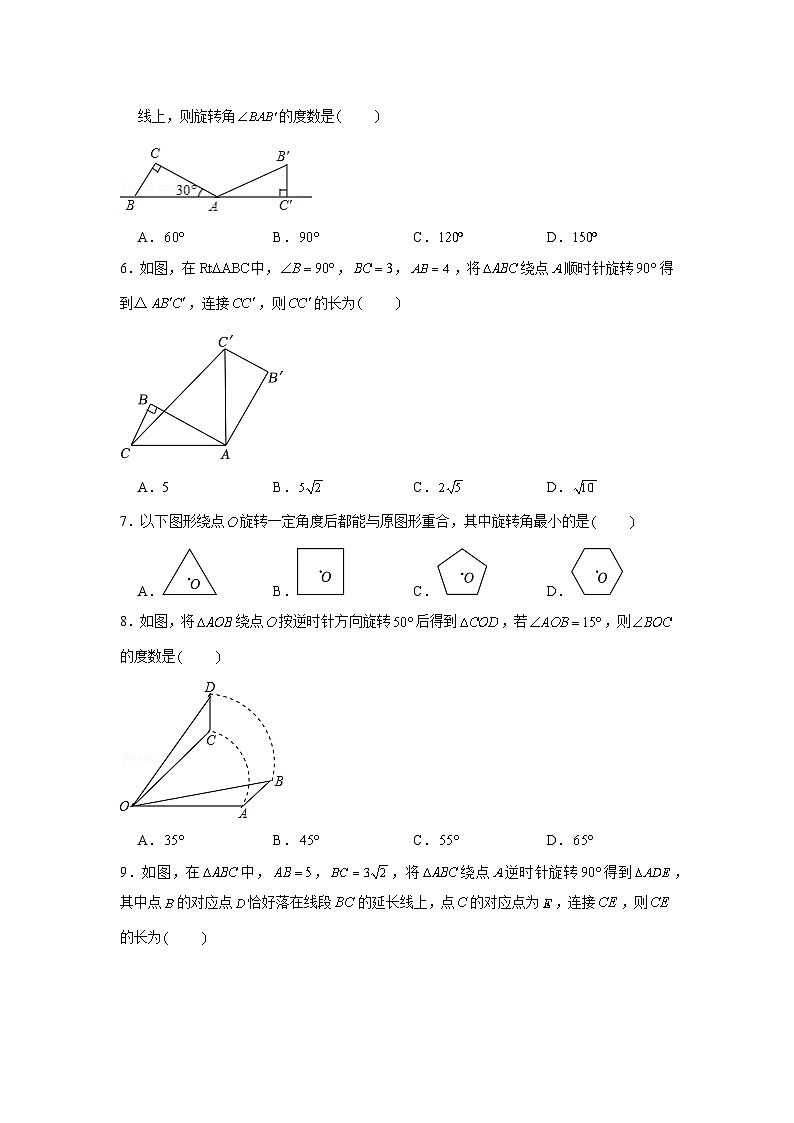
23.1图形的旋转【素养基础达标】2023-2024学年人教版数学九年级上册  基础知识梳理1.旋转的定义定义把一个平面图形绕平面内某一点O转动一个角度，叫做图形的旋转旋转三要素①旋转中心：点O叫做旋转中心.②旋转方向：分为顺时针与逆时针.③旋转角：转动的角叫做旋转角对应元素对应点、对应角、对应线段旋转的性质①对应点到旋转中心的距离相等；②对应点与旋转中心所连线段的夹角等于旋转角；③旋转前、后的图形全等.确定旋转中心的位置两组对应点所连线段的垂直平分线的交点即为旋转中心.旋转作图步骤①连接并转动：连接关键点与旋转中心，并把连线绕旋转中心旋转一定角度；②截：截取相等线段，找到对称点；③连：顺次连接对称点；  素养基础达标一．选择题（共10小题）1．如图，在中，，将绕点逆时针旋转得到，点，的对应点分别为，．当点、、在同一条直线上时，下列结论不正确的是　　A． B． C． D．2．如图，将木条，与钉在一起，，，要使木条与平行，木条需顺时针旋转的最小度数是　　A． B． C． D．3．如图，将绕顶点逆时针旋转到，，，则的度数为　　A． B． C． D．4．如图，在中，，，，将绕点逆时针旋转得到，点落在线段上，则、两点间的距离为　　A． B． C．6 D．5．如图，将一个含角的直角三角板绕点旋转，得点，，，在同一条直线上，则旋转角的度数是　　A． B． C． D．6．如图，在中，，，，将绕点顺时针旋转得到△，连接，则的长为　　A．5 B． C． D．7．以下图形绕点旋转一定角度后都能与原图形重合，其中旋转角最小的是　　A． B． C． D．8．如图，将绕点按逆时针方向旋转后得到，若，则的度数是　　A． B． C． D．9．如图，在中，，，将绕点逆时针旋转得到，其中点的对应点恰好落在线段的延长线上，点的对应点为，连接，则的长为　　A． B． C． D．10．如图，在中，，，将绕点按顺时针方向旋转到△的位置，使得点，，在同一条直线上，那么旋转角的度数为　　A． B． C． D．二．填空题（共8小题）11．如图，将点绕着原点逆时针方向旋转得到点，则点的坐标是 　　．12．如图，绕点逆时针旋转得到，点、的对应点分别是点和点，，则的度数为 　　．13．如图，该图形绕其中心旋转能与其自身完全重合，则其旋转角最小为 　　度．14．如图，将线段绕点按顺时针方向旋转，得到线段，则　　15．如图，将三角形绕点按逆时针方向旋转后得到三角形，若，则　　．16．如图，在中，，，，将绕点顺时针旋转得到，当点的对应点恰好落在边上时，的长为 　　．17．如图，在中，，为边上一点，且点到的距离等于点到的距离．将绕点旋转得到△，连接，．若，则的值为　　．18．如图，中，．将绕点逆时针旋转得到△．若，，则　　．三．解答题（共8小题）19．如图，是等边三角形，点在边上，将绕点旋转得到．（1）求证：是等边三角形；（2）若，，求的周长．20．如图，将绕直角顶点按逆时针方向旋转得到．已知，求的度数．21．如图，在中，，，将绕点顺时针方向旋转至的位置，连接，作平分交于点，连接交于点．（1）求证是等边三角形；（2）求证：．22．如图1，正方形的边长为5，点为正方形边上一动点，过点作于点，将绕点逆时针旋转得，连接．（1）证明：．（2）延长交于点．判断四边形的形状，并说明理由；（3）若，求线段的长度23．已知为等边三角形，是射线上的一动点，连接，将绕点顺时针方向旋转得到，连接，．（1）如图1，的形状为 　　．（2）试猜想线段，，之间的数量关系，并说明理由．24．如图，将正方形绕点逆时针旋转得到正方形，与相交于点，连接，若，求长．25．如图，在中，，，将绕点顺时针旋转，得到，点、的对应点分别是、．为的中点，连接、、、与相交于点，与相交于点．（1）求证：是等边三角形；（2）求证：四边形为平行四边形．26．和都是等边三角形．将绕点旋转到图①的位置时，连接，并延长相交于点（点与点重合），有（或成立（不需证明）；（1）将绕点旋转到图②的位置时，连接，相交于点，连接，猜想线段、、之间有怎样的数量关系？并加以证明；（2）将绕点旋转到图③的位置时，连接，相交于点，连接，猜想线段、、之间有怎样的数量关系？并加以证明．
23.1图形的旋转【素养基础达标】2023-2024学年人教版数学九年级上册  基础知识梳理1.旋转的定义定义把一个平面图形绕平面内某一点O转动一个角度，叫做图形的旋转旋转三要素①旋转中心：点O叫做旋转中心.②旋转方向：分为顺时针与逆时针.③旋转角：转动的角叫做旋转角对应元素对应点、对应角、对应线段旋转的性质①对应点到旋转中心的距离相等；②对应点与旋转中心所连线段的夹角等于旋转角；③旋转前、后的图形全等.确定旋转中心的位置两组对应点所连线段的垂直平分线的交点即为旋转中心.旋转作图步骤①连接并转动：连接关键点与旋转中心，并把连线绕旋转中心旋转一定角度；②截：截取相等线段，找到对称点；③连：顺次连接对称点；  素养基础达标一．选择题（共10小题）1．如图，在中，，将绕点逆时针旋转得到，点，的对应点分别为，．当点、、在同一条直线上时，下列结论不正确的是　　A． B． C． D．【答案】【分析】根据图形旋转的性质，以及全等图形的基本性质进行逐项分析即可．【解答】解：由旋转的性质可知，，故选项不符合题意；则，且、、三点在同一直线上，，由旋转的性质知，，则，，故选项不符合题意；中，，，故选项不符合题意；，，，故选项符合题意；故选：．2．如图，将木条，与钉在一起，，，要使木条与平行，木条需顺时针旋转的最小度数是　　A． B． C． D．【答案】【分析】根据同位角相等两直线平行，求出旋转后的同位角的度数，然后用减去即可得到木条旋转的度数．【解答】解：如图，时，，要使木条与平行，木条旋转的度数至少是．故选：．3．如图，将绕顶点逆时针旋转到，，，则的度数为　　A． B． C． D．【答案】【分析】由旋转的性质及，得出，，由，求出，再根据三角形内角和定理即可求出的度数．【解答】解：将绕顶点逆时针旋转到，，，，，，，故选：．4．如图，在中，，，，将绕点逆时针旋转得到，点落在线段上，则、两点间的距离为　　A． B． C．6 D．【答案】【分析】首先利用勾股定理求出的长，再根据旋转的性质得和的长，最后利用勾股定理求出即可．【解答】解：将绕点逆时针旋转得到，，，在中，，，，在中，由勾股定理得，，故选：．5．如图，将一个含角的直角三角板绕点旋转，得点，，，在同一条直线上，则旋转角的度数是　　A． B． C． D．【分析】根据旋转角的定义，两对应边的夹角就是旋转角，即可求解．【解答】解：旋转角是．故选：．6．如图，在中，，，，将绕点顺时针旋转得到△，连接，则的长为　　A．5 B． C． D．【答案】【分析】在中，由勾股定理解得的长，再根据旋转的性质得到，，，在中再利用勾股定理解得的长即可．【解答】解：，，，在中，，由旋转的性质得，，在中，．故选：．7．以下图形绕点旋转一定角度后都能与原图形重合，其中旋转角最小的是　　A． B． C． D．【答案】【分析】求出各旋转对称图形的最小旋转角度，继而可作出判断．【解答】解：、最小旋转角度；、最小旋转角度；、最小旋转角度；、最小旋转角度；故选：．8．如图，将绕点按逆时针方向旋转后得到，若，则的度数是　　A． B． C． D．【答案】【分析】首先根据旋转变换的性质求出的度数，结合，即可解决问题．【解答】解：由题意及旋转变换的性质得：，，，故选：．9．如图，在中，，，将绕点逆时针旋转得到，其中点的对应点恰好落在线段的延长线上，点的对应点为，连接，则的长为　　A． B． C． D．【答案】【分析】根据旋转的性质，易得为等腰直角三角形，为直角三角形，利用勾股定理进行求解即可．【解答】解：旋转，，，，，，，故选：．10．如图，在中，，，将绕点按顺时针方向旋转到△的位置，使得点，，在同一条直线上，那么旋转角的度数为　　A． B． C． D．【答案】【分析】先判断出旋转角最小是，根据直角三角形的性质计算出，再由旋转的性质即可得出结论．【解答】解：绕点按顺时针方向旋转到△的位置，使得点、、在同一条直线上，旋转角最小是，，，，△由旋转而成，，，故选：．二．填空题（共8小题）11．如图，将点绕着原点逆时针方向旋转得到点，则点的坐标是 　　．【答案】．【分析】依据题意，在平面直角坐标系，确定点的位置，再由特殊角的关系即可求出的坐标．【解答】解：点绕着原点逆时针方向旋转得到点，在第二象限．如图，作轴于．，．．，．．故答案为：．12．如图，绕点逆时针旋转得到，点、的对应点分别是点和点，，则的度数为 　　．【答案】．【分析】根据旋转角的定义得，再利用角的和差定义求解即可．【解答】解：由旋转的性质可知，，，，故答案为：．13．如图，该图形绕其中心旋转能与其自身完全重合，则其旋转角最小为 　60　度．【答案】60．【分析】观察图形可得，图形由六个形状相同的部分组成，从而能计算出旋转角度．【解答】解：图形可看作由一个基本图形每次旋转，旋转6次所组成，故最小旋转角为．故答案为：60．14．如图，将线段绕点按顺时针方向旋转，得到线段，则　　【答案】．【分析】由旋转的性质可得，，由等腰三角形的性质可求解．【解答】解：将线段绕点按顺时针方向旋转，，，，故答案为：．15．如图，将三角形绕点按逆时针方向旋转后得到三角形，若，则　　．【答案】．【分析】由旋转的性质可得，即可求解．【解答】解：将三角形绕点按逆时针方向旋转后得到三角形，，，故答案为：．16．如图，在中，，，，将绕点顺时针旋转得到，当点的对应点恰好落在边上时，的长为 　3　．【答案】3．【分析】根据旋转变换的性质得到，根据等边三角形的性质解答即可．【解答】解：由旋转的性质可知，，，，为等边三角形，，，故答案为：3．17．如图，在中，，为边上一点，且点到的距离等于点到的距离．将绕点旋转得到△，连接，．若，则的值为　　．【分析】连接、，过点作于点，如图，根据旋转的性质得，，，则可证明，根据相似三角形的性质得，则可设，，然后利用等腰直角三角形的性质得，接着利用勾股定理计算出，则可求出答案．【解答】解：连接、，过点作于点，如图，绕点旋转得到△，，，，即，，，设，，点到的距离等于点到的距离，，，在中，，，即．故答案为：．18．如图，中，．将绕点逆时针旋转得到△．若，，则　5　．【答案】5．【分析】由旋转的性质可得，，，可证是等边三角形，可得，由勾股定理可求解．【解答】解：将绕点逆时针旋转得到△，，，，是等边三角形，，，，，故答案为：5．三．解答题（共8小题）19．如图，是等边三角形，点在边上，将绕点旋转得到．（1）求证：是等边三角形；（2）若，，求的周长．【答案】（1）证明见解答过程；（2）15．【分析】（1）由旋转的性质可得，，可得，可证；（2）由旋转的性质可得，即可求的周长．【解答】（1）证明：是等边三角形，，，将绕点旋转得到．，，是等边三角形；（2）解：将绕点旋转得到．，的周长，的周长．20．如图，将绕直角顶点按逆时针方向旋转得到．已知，求的度数．【分析】根据旋转的性质可得，再根据三角形的内角和定理求得结果．【解答】解：绕其直角顶点按逆时针方向旋转后得到，，，．21．如图，在中，，，将绕点顺时针方向旋转至的位置，连接，作平分交于点，连接交于点．（1）求证是等边三角形；（2）求证：．【答案】（1）证明见解析；（2）证明见解析．【分析】（1）由旋转的性质得出，，，则等边三角形的判定可得出结论；（2）证明，得出，证出，则可得出结论．【解答】（1）证明：将绕点顺时针方向旋转至的位置，，，，，，，，是等边三角形；（2）证明：平分，，，，，，将绕点顺时针方向旋转至的位置，，，．22．如图1，正方形的边长为5，点为正方形边上一动点，过点作于点，将绕点逆时针旋转得，连接．（1）证明：．（2）延长交于点．判断四边形的形状，并说明理由；（3）若，求线段的长度【答案】（1）证明见解答过程；（2）正方形，理由见解答过程；（3）3．【分析】（1）由旋转的性质证明，即可得出答案；（2）先证明四边形是矩形，根据邻边相等的矩形是正方形即可证明；（3）设正方形边长为，在△中用勾股定理即可求解．【解答】（1）证明：由题意和旋转的性质可得：，，四边形是正方形，，，，，即：，，，，，；（2）解：四边形是正方形，理由如下：由（1）得：，且，，，四边形是矩形，，四边形是正方形；（3）解：在正方形中，，在正方形中，设，，则，在△中，，，即：，解得：（不符合题意，舍去），，，，故答案为：3．23．已知为等边三角形，是射线上的一动点，连接，将绕点顺时针方向旋转得到，连接，．（1）如图1，的形状为 　等边三角形　．（2）试猜想线段，，之间的数量关系，并说明理由．【答案】（1）等边三角形；（2）①当点在线段上时，，理由见解析过程；②当点在线段的延长线上时，，理由见解析过程．【分析】（1）根据旋转，得到，，即可得出结论；（2）分点在线段上和点在线段的延长线上，两种情况讨论求解即可．【解答】（1）解：将绕点顺时针方向旋转得到，，，是等边三角形；故答案为：等边三角形．（2）解：①当点在线段上时，．理由：由旋转的性质可知，．是等边三角形，，，，，即．在和中，，，，．②如图，当点在线段的延长线上时，．理由：由旋转的性质可知，．是等边三角形，，，，，即．在和中，，，，．24．如图，将正方形绕点逆时针旋转得到正方形，与相交于点，连接，若，求长．【答案】6．【分析】根据旋转的性质可知：，，再证明，即有，，进而可得，在中，可得．【解答】解：在正方形和正方形中，，，，根据旋转的性质可知：，，，，，，，，，在中，，，，故答案为：6．25．如图，在中，，，将绕点顺时针旋转，得到，点、的对应点分别是、．为的中点，连接、、、与相交于点，与相交于点．（1）求证：是等边三角形；（2）求证：四边形为平行四边形．【答案】（1）见解析过程；（2）见解析过程．【分析】（1）由直角三角形的性质可得，，可得结论；（2）由旋转的性质可得，，，可证，由“”可证，可得，可得结论．【解答】证明：（1）点是边中点，，，，，，，是等边三角形；（2）将绕点顺时针旋转，得到，，，，，为等边三角形，，点为的边的中点，，，在和中，，，，，且，四边形是平行四边形．26．和都是等边三角形．将绕点旋转到图①的位置时，连接，并延长相交于点（点与点重合），有（或成立（不需证明）；（1）将绕点旋转到图②的位置时，连接，相交于点，连接，猜想线段、、之间有怎样的数量关系？并加以证明；（2）将绕点旋转到图③的位置时，连接，相交于点，连接，猜想线段、、之间有怎样的数量关系？并加以证明．【答案】（1），理由见解析；（2），理由见解析．【分析】（1）证明和，得，，再证明是等边三角形，最后由线段的和可得结论；（2）如图③，在上截取，连接，同理可得结论．【解答】解：（1），理由如下：如图②，在上截取，连接，、都是等边三角形，，，，，即，，，，，，，，，是等边三角形，，；（2），理由如下：如图③，在上截取，连接，同理得：，，，，，，，，是等边三角形，，．