




初中数学浙教版八年级上册第2章 特殊三角形2.1 图形的轴对称授课ppt课件
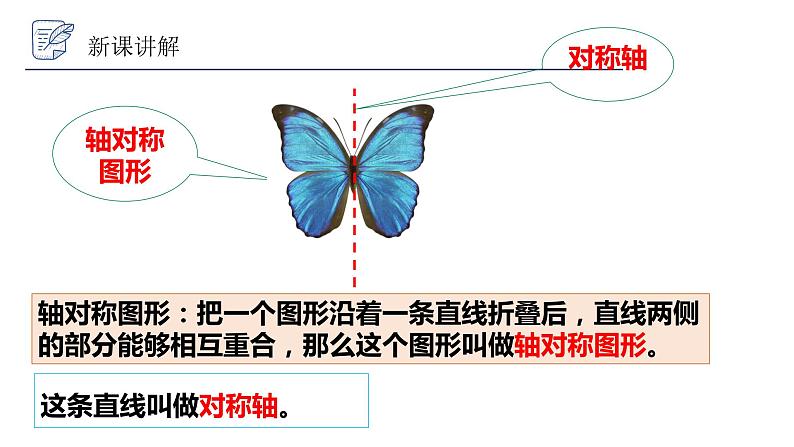
展开沿着一条直线折叠后,直线两侧的部分能够相互重合
轴对称图形:把一个图形沿着一条直线折叠后,直线两侧的部分能够相互重合,那么这个图形叫做轴对称图形。
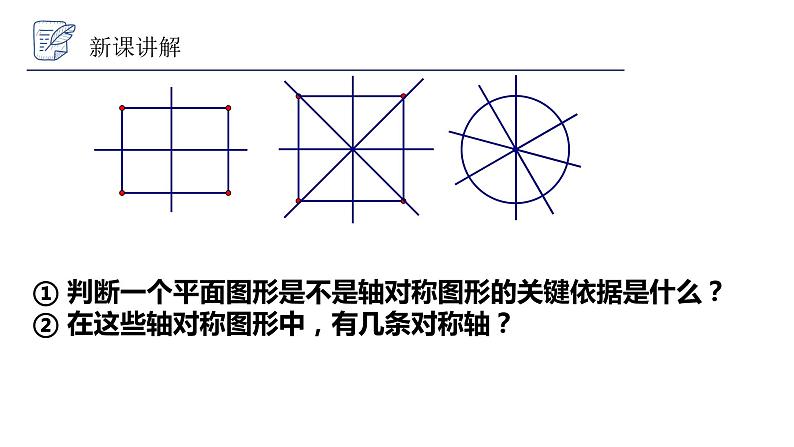
① 判断一个平面图形是不是轴对称图形的关键依据是什么? ② 在这些轴对称图形中,有几条对称轴?
1.下列图形是轴对称图形吗?你是怎么判别的?
对于以上各轴对称图形,你能找出对称轴吗?有哪些方法?
是轴对称图形,根据轴对称图形的定义,沿一条直线折叠,直线两侧的图形可以重合
如图为各图形的对称轴,用对折的方法
下列四个图案,其中轴对称图形有( )
A.0个 B.1个 C.2个 D.3个
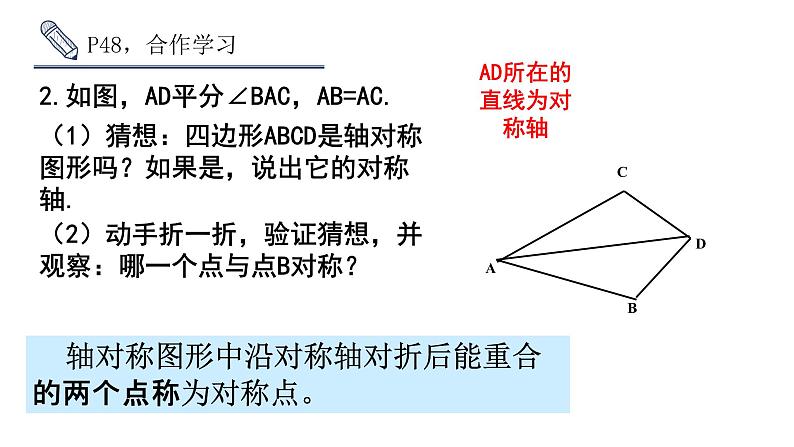
2.如图,AD平分∠BAC,AB=AC.
AD所在的直线为对称轴
(1)猜想:四边形ABCD是轴对称图形吗?如果是,说出它的对称轴.
(2)动手折一折,验证猜想,并观察:哪一个点与点B对称?
轴对称图形中沿对称轴对折后能重合的两个点称为对称点。
2.如图,AD平分∠BAC,AB=AC.连结BC,交AD于点E.
(6)由AC=AB,CD=BD,可得对称轴AD与对称点的连线BC有何关系?尝试概括。
(4)把四边形ABCD沿AD对折,图中重合的线段有哪些?
(5)图中重合的角有哪些?
对称轴垂直平分连结两个对称点的线段
如图,已知△ABC和直线m。以直线m 为对称轴,求作以点A,B,C的对称点A’,B’,C’为顶点的△ A’B’C’
几何图形都可以看做由点组成,找:描点:连线:
从各关键点作对称轴的垂线;延长这个垂线,在对称轴另外一边,找一个点到这个垂直交点的距离和这边的一样长;
按照已知图形的形状,依次地把各对应点连结起来。
已知对称轴 和线段AB,画出线段AB关于直线l的对称点A′B′。
图形的轴对称有下面的性质: 1、成轴对称的图形不改变原图形的形状和大小. 2、成轴对称的两个图形是全等图形.
请同学们观察例1画的两个三角形,以及下面几组图形,有什么共同特征?
轴对称和轴对称图形的区别和联系
例2 如图,直线l表示草原上的一条河流.一骑马少年从A地出发,去河边让马饮水,然后返回位于B地的家中. 他沿怎样的路线行走,能使路程最短?作出这条最短路线.
思考:
2.A,B两点连线是否经过l上一点?为什么?
3.l的另一侧是否存在点A',使l上的任意一点P满足PA=PA'?此时点A与A'有何位置关系?
4.由此,你能顺利解决问题了吗?
1.关于“最短”,你学过哪些相关知识?
设P是直线l上任意一点,连结AP,A’P由作图知,直线l垂直平分AA’则AC=A’C,AP=A’P(线段垂直平分线上的点到线段两端的距离相等)∴ AP+BP=A’P+BP≥A’BA’B=A’C+BC=AC+BC即AP+BP≥AC+BC所以沿折线A-C-B的路线行走时路程最短。
作点A关于直线l的对称点A’,连结A’B, 交直线l于点C,连结AC,骑马少年沿折线A-C-B的路线行走时路程最短.
类型1 一线异侧两点
解决问题步骤1、作对称点:作点关于直线的对称点(垂直平分);2、转化:运用轴对称把直线同侧的两点转化为直线异侧的两点;3、连线:两点之间,线段最短。
类型2 一线同侧两点
在∠ABC内有一点P,问:能否在BA,BC边上各找到一点M,N,使△PMN的周长最短?若能,请画图说明;若不能,说明理由.
解决问题步骤1、分别作这点关于两线的对称点;2、连接两对称点交两线于两点,交点即为所求。
1.观察下列图形,从图案看是轴对称图形的有( )
2、如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;(2)在DE上画出点Q,使QA+QC最小;(3)四边形BCC1B1的面积为 .
初中数学青岛版八年级上册2.1 图形的轴对称背景图ppt课件: 这是一份初中数学青岛版八年级上册2.1 图形的轴对称背景图ppt课件,共20页。PPT课件主要包含了学习目标,新课引入,实验与探究,直线l即为对称轴,例题讲解,随堂练习,cm2等内容,欢迎下载使用。
初中数学浙教版八年级上册2.1 图形的轴对称完整版ppt课件: 这是一份初中数学浙教版八年级上册2.1 图形的轴对称完整版ppt课件,文件包含浙教版数学八上21图形的轴对称课件pptx、浙教版数学八上21图形的轴对称练习docx、浙教版数学八上21图形的轴对称教案doc等3份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
初中数学浙教版八年级上册2.1 图形的轴对称备课课件ppt: 这是一份初中数学浙教版八年级上册2.1 图形的轴对称备课课件ppt,共26页。PPT课件主要包含了请你试一试,一条对称轴,两条对称轴,三条对称轴,四条对称轴,无数条对称轴,请你想一想,所在的直线,合作学习,请说出它的对称轴等内容,欢迎下载使用。













