


还剩11页未读,
继续阅读
初中数学浙教版八年级上册第2章 特殊三角形2.4 等腰三角形的判定定理教案配套课件ppt
展开
这是一份初中数学浙教版八年级上册第2章 特殊三角形2.4 等腰三角形的判定定理教案配套课件ppt,共19页。PPT课件主要包含了新知讲授,基础练习,练习2,闯关练习,第一关,第三关提高题等内容,欢迎下载使用。
小明在作图时,不小心把一块30°, 60°,90°的三角板掉到了地上,断裂成了两部分。爱探索的他发现断裂开的其中一部分刚好是一个三角形,于是他用量角器量得其中有两个角刚好都是30°,神奇的是该三角形中含30°角的两边刚好相等,你能帮小明解释一下吗?
下面我们一起来探究一下这个问题。
在纸上任意画线段BC,分别以点B和点C为顶点,以BC为一边,在BC的同侧画两个相等的角,两角的另一边相交于点A。1、量一量,线段AB与AC相等吗?2、其他同学的结果与你的相同吗?你发现了什么规律?
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
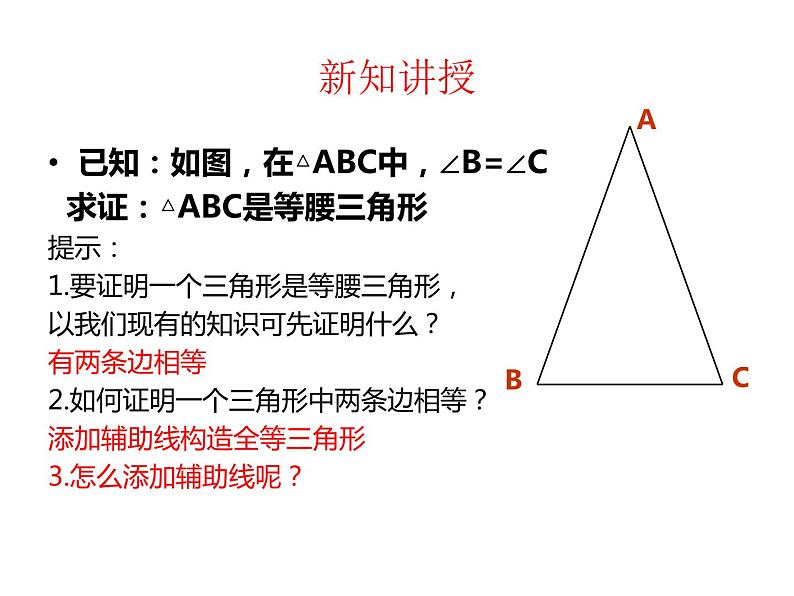
已知:如图,在△ABC中,∠B=∠C 求证:△ABC是等腰三角形提示:1.要证明一个三角形是等腰三角形,以我们现有的知识可先证明什么?有两条边相等2.如何证明一个三角形中两条边相等?添加辅助线构造全等三角形3.怎么添加辅助线呢?
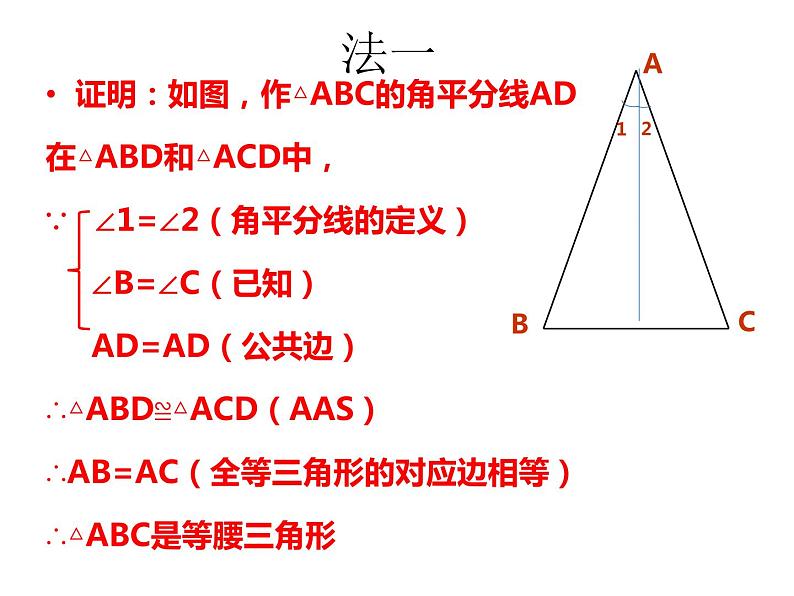
证明:如图,作△ABC的角平分线AD在△ABD和△ACD中,∵ ∠1=∠2(角平分线的定义) ∠B=∠C(已知) AD=AD(公共边)∴△ABD≌△ACD(AAS)∴AB=AC(全等三角形的对应边相等)∴△ABC是等腰三角形
在△ ABD和△ ACD中
∴ΔABD≌ΔACD(AAS)
解:过A作AD垂直BC于D
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
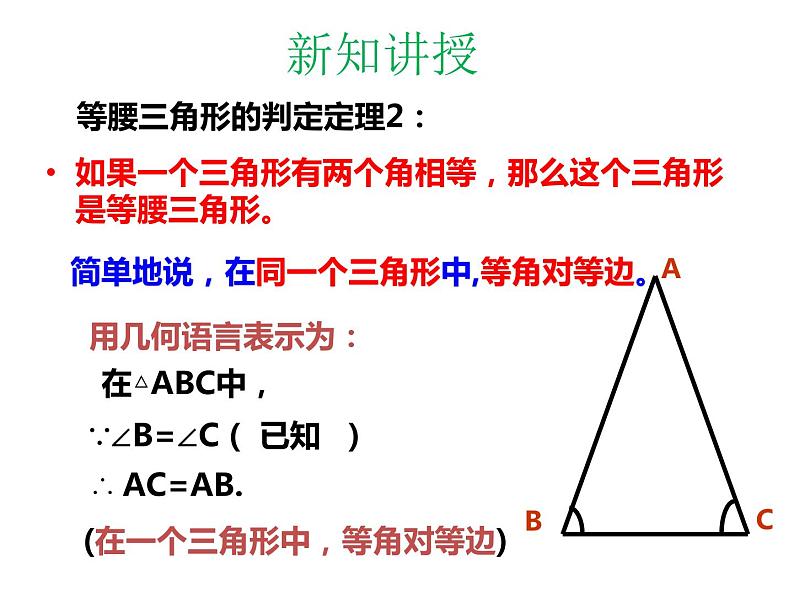
等腰三角形的判定定理2:
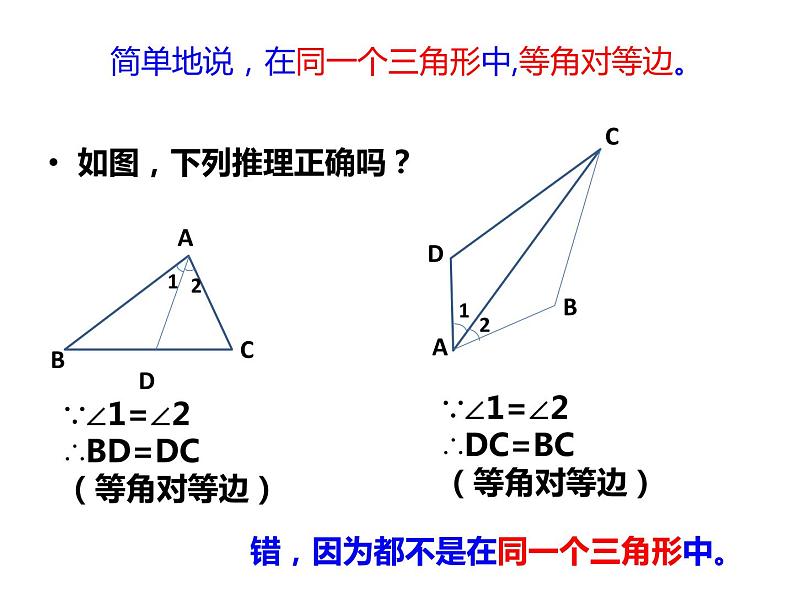
简单地说,在同一个三角形中,等角对等边。
∵∠B=∠C ( 已知 )
∴ AC=AB. (在一个三角形中,等角对等边)
简单地说,在同一个三角形中,等角对等边。
如图,下列推理正确吗?
∵∠1=∠2∴BD=DC(等角对等边)
∵∠1=∠2∴DC=BC(等角对等边)
错,因为都不是在同一个三角形中。
练习1. (课内练习1)已知一个三角形的两个角的度数分别是43°,94°,这个三角形是不是等腰三角形?请说明理由。
如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 图中的等腰三角形有 .
上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°, ∠NBC=80°,求从B处到灯塔C的距离。
解:∵∠NBC=∠A+∠C∴∠C=80°- 40°= 40° ∴ BA=BC(等角对等边)∵AB=20(12-10)=40∴BC=40答:B处到达灯塔C40海里
若 ∠NAC=25°, ∠NBC=50°,求从B处到灯塔C的距离。
若 ∠NAC=60°, ∠NBC=120°呢?
若 ∠NAC= ,∠NBC=2 呢?你发现了什么?
你还有其它方法测量河宽吗?
有两边相等的三角形是等腰三角形
2.在同一个三角形中,等边对等角
3.等腰三角形三线合一
从边的角度:定义:有两边相等的三角形是等腰三角形
2.从角的角度:在同一个三角形中,等角对等边
1.三个角都相等的三角形是等边三角形.
已知:如图,在△ABC中,∠A=∠B=∠C. 求证:△ABC为等边三角形.
2.有一个角是60°的等腰三角形是等边三角形.
已知:如图,在△ABC中,AB=AC,∠B=60°.求证:△ABC为等边三角形.
第一种情况:有一个底角是60°
三个角都相等的三角形是等边三角形.
第二种情况:顶角是60°
已知:如图,在△ABC中,AB=AC,∠A=60°.求证:△ABC为等边三角形.
如图,D是AC上的一点.
(1) 若∠A=∠ABD,则________=_______
(2) 若CB=CD,则∠_______=∠_______
第二关:已知:AD平分∠EAC,AD//BC,△ABC是等腰三角形吗?请说明理由.
1、已知正方形ABCD和等边三角形EAD,试求∠BEC的度数。
小明在作图时,不小心把一块30°, 60°,90°的三角板掉到了地上,断裂成了两部分。爱探索的他发现断裂开的其中一部分刚好是一个三角形,于是他用量角器量得其中有两个角刚好都是30°,神奇的是该三角形中含30°角的两边刚好相等,你能帮小明解释一下吗?
下面我们一起来探究一下这个问题。
在纸上任意画线段BC,分别以点B和点C为顶点,以BC为一边,在BC的同侧画两个相等的角,两角的另一边相交于点A。1、量一量,线段AB与AC相等吗?2、其他同学的结果与你的相同吗?你发现了什么规律?
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
已知:如图,在△ABC中,∠B=∠C 求证:△ABC是等腰三角形提示:1.要证明一个三角形是等腰三角形,以我们现有的知识可先证明什么?有两条边相等2.如何证明一个三角形中两条边相等?添加辅助线构造全等三角形3.怎么添加辅助线呢?
证明:如图,作△ABC的角平分线AD在△ABD和△ACD中,∵ ∠1=∠2(角平分线的定义) ∠B=∠C(已知) AD=AD(公共边)∴△ABD≌△ACD(AAS)∴AB=AC(全等三角形的对应边相等)∴△ABC是等腰三角形
在△ ABD和△ ACD中
∴ΔABD≌ΔACD(AAS)
解:过A作AD垂直BC于D
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
等腰三角形的判定定理2:
简单地说,在同一个三角形中,等角对等边。
∵∠B=∠C ( 已知 )
∴ AC=AB. (在一个三角形中,等角对等边)
简单地说,在同一个三角形中,等角对等边。
如图,下列推理正确吗?
∵∠1=∠2∴BD=DC(等角对等边)
∵∠1=∠2∴DC=BC(等角对等边)
错,因为都不是在同一个三角形中。
练习1. (课内练习1)已知一个三角形的两个角的度数分别是43°,94°,这个三角形是不是等腰三角形?请说明理由。
如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 图中的等腰三角形有 .
上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°, ∠NBC=80°,求从B处到灯塔C的距离。
解:∵∠NBC=∠A+∠C∴∠C=80°- 40°= 40° ∴ BA=BC(等角对等边)∵AB=20(12-10)=40∴BC=40答:B处到达灯塔C40海里
若 ∠NAC=25°, ∠NBC=50°,求从B处到灯塔C的距离。
若 ∠NAC=60°, ∠NBC=120°呢?
若 ∠NAC= ,∠NBC=2 呢?你发现了什么?
你还有其它方法测量河宽吗?
有两边相等的三角形是等腰三角形
2.在同一个三角形中,等边对等角
3.等腰三角形三线合一
从边的角度:定义:有两边相等的三角形是等腰三角形
2.从角的角度:在同一个三角形中,等角对等边
1.三个角都相等的三角形是等边三角形.
已知:如图,在△ABC中,∠A=∠B=∠C. 求证:△ABC为等边三角形.
2.有一个角是60°的等腰三角形是等边三角形.
已知:如图,在△ABC中,AB=AC,∠B=60°.求证:△ABC为等边三角形.
第一种情况:有一个底角是60°
三个角都相等的三角形是等边三角形.
第二种情况:顶角是60°
已知:如图,在△ABC中,AB=AC,∠A=60°.求证:△ABC为等边三角形.
如图,D是AC上的一点.
(1) 若∠A=∠ABD,则________=_______
(2) 若CB=CD,则∠_______=∠_______
第二关:已知:AD平分∠EAC,AD//BC,△ABC是等腰三角形吗?请说明理由.
1、已知正方形ABCD和等边三角形EAD,试求∠BEC的度数。













