2024届高考数学一轮复习第2章思维深化微课堂嵌套函数的零点问题课件

这是一份2024届高考数学一轮复习第2章思维深化微课堂嵌套函数的零点问题课件，共13页。

高考中针对函数零点的个数或范围这一知识点，常考查分段函数与复合函数的相关问题．对于嵌套函数的零点问题，通常先“换元解套”，将复合函数拆解为两个相对简单的函数，借助函数的图象、性质求解．
嵌套函数零点个数的解题步骤(1)换元解套，转化为t＝g(x)与y＝f(t)的零点．(2)依次解方程，令f(t)＝0，求t，代入t＝g(x)，求出x的值或判断图象交点个数．
[思维架桥]　利用导数得到函数f(x)的单调性和最值，即可画出大致图象．令t＝f(x)，得到方程t2＋mt＋m－1＝0的根，然后分情况讨论，可得m的范围．
解嵌套函数零点问题的步骤(1)换元，令t＝f(x)，y＝g(t)，f(x)为“内函数”，g(t)为“外函数”．(2)作图，作“外函数”y＝g(t)的图象与“内函数”t＝f(x)的图象．(3)观察图象进行分析．
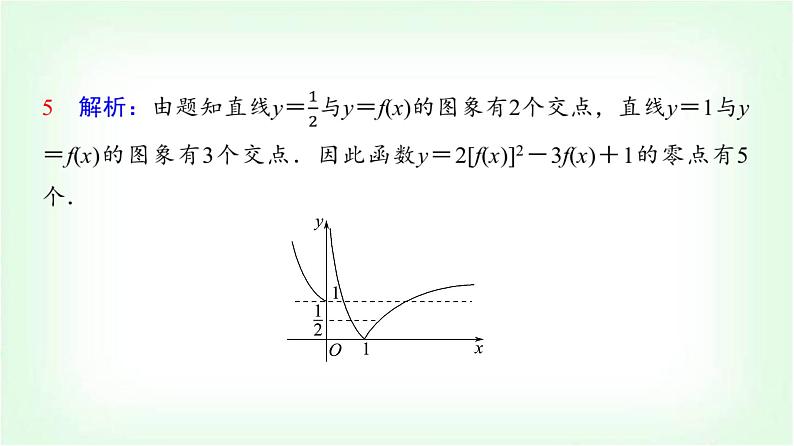
[－1，＋∞)　解析：设t＝f(x)，令f(f(x))－a＝0，则a＝f(t)．在同一坐标系内作y＝a，y＝f(t)的图象(如图)．当a≥－1时，y＝a与y＝f(t)的图象有两个交点．
设交点的横坐标为t1，t2(不妨设t2>t1)，则t1<－1，t2≥－1.当t1<－1时，t1＝f(x)有一解；当t2≥－1时，t2＝f(x)有两解．综上，当a≥－1时，函数g(x)＝f(f(x))－a有三个不同的零点．