人教版八年级数学上册期末综合训练课件

这是一份人教版八年级数学上册期末综合训练课件，共36页。PPT课件主要包含了3x－52，BE＝CF等内容，欢迎下载使用。
一、选择题(本大题共10小题，每小题3分，共30分)1. 下列出版社的商标图案中，是轴对称图形的为( )
2. 下列计算正确的是( )A. a2＋b3＝2a5B. a4÷a＝a4C. a2·a4＝a8D. (－a2)3＝－a6
3. 唐代刘禹锡有诗曰：“庭前芍药妖无格，池上芙蕖净少情．唯有牡丹真国色，花开时节动京城”.牡丹是河南洛阳的市花，有非常高的观赏价值．某品种的牡丹花粉直径约为0.000 035 4 m，则数据0.000 035 4用科学记数法表示为( )A. 3.54×10－5B. 0.354×10－6C. 3.54×10－7D. 35.4×10－6
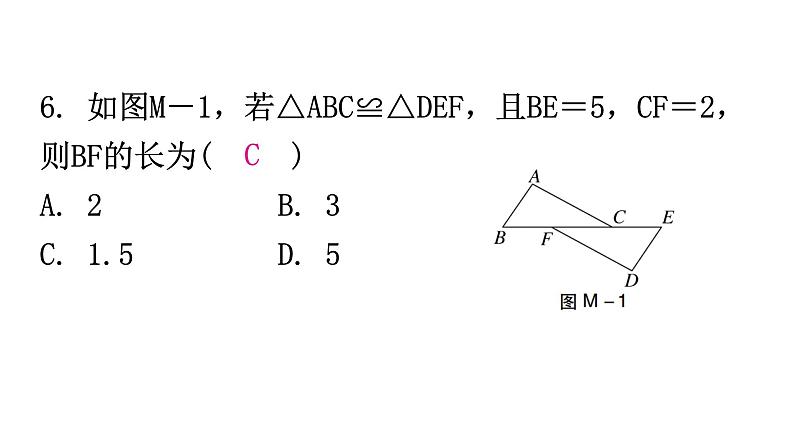
6. 如图M－1，若△ABC≌△DEF，且BE＝5，CF＝2，则BF的长为( )A. 2B. 3C. 1.5D. 5
7. 如图M－2，A，B，C表示三个居民小区，为丰富居民们的文化生活，现准备建一个文化广场，使它到三个小区的距离相等，则文化广场应建在( )A. AC，BC两边高线的交点处B. AC，BC两边中线的交点处C. ∠A，∠B两内角平分线的交点处D. AC，BC两边垂直平分线的交点处
8. 如图M－3，AD∥BC，BG，AG分别平分∠ABC与∠BAD，GH⊥AB，若GH＝5，则AD与BC之间的距离是( )A. 5B. 8C. 10D. 15
9. 如图M－4，△ABC的面积为1 cm2，AP垂直∠ABC的平分线BP于点P，则△PBC的面积为( )A. 0.4 cm2B. 0.5 cm2C. 0.6 cm2D. 0.7 cm2
10. 如图M－5，在△ABC中，∠BAC＝60°，∠BAC的平分线AD与边BC的垂直平分线MD相交于点D，DE⊥AB交AB的延长线于点E，DF⊥AC于点F，有下列结论：①DE＝DF；②DE＋DF＝AD；③DM平分∠EDF；④AB＋AC＝2AE；其中正确的有( )A. 1个B. 2个C. 3个D. 4个
二、填空题(本大题共5小题，每小题3分，共15分)11. 一个多边形的内角和与外角和之和为2 520°，则这个多边形的边数为__________. 12. 已知点A(a，2 019)与点B(2 020，b)关于y轴对称，则a＋b的值为__________.
13. 分解因式：4mx2－my2＝___________________.14. 已知2m＝5，22m＋n＝45，则2n＝__________.
m(2x＋y)(2x－y)
15. 如图M－6，在△ABC中，AB＝AC，点D和E分别是边BC和AC上的点，且满足DB＝DA＝DE，若∠CDE＝50°，则∠BAC的度数为__________°.
三、解答题(一)(本大题共3小题，第16题10分，第17、18题各7分，共24分)16. （1）化简：(3m＋n)2－3m(m＋2n).
解：原式＝(9m2＋6mn＋n2)－(3m2＋6mn)＝9m2＋6mn＋n2－3m2－6mn＝6m2＋n2.
17. 如图M－7，在△ABC中，AD⊥BC于点D，BE是△ABC的角平分线，交AD于点F.若∠ABC＝40°，求∠AFE的度数.
18. 某学校开展了社会实践活动，活动地点距离学校12 km，甲、乙两同学骑自行车同时从学校出发，甲的速度是乙的1.2倍，结果甲比乙早到10 min，求乙骑自行车的速度．
四、解答题(二)(本大题共3小题，每小题9分，共27分)19. 如图M－8，在△ABC中，∠BAC＝90°．（1）尺规作图：作BC边上的高，垂足为D（保留作图痕迹，不写作法）；（2）若∠C＝30°，AB＝2，求BD的长．
21. 综合与实践主题：制作无盖长方体容器.材料：一张长和宽分别为50 cm和30 cm的长方形纸板.制作步骤：将长方形纸板的四个角剪去四个边长相同的小正方形纸板（如图M－9①），然后折成无盖长方体容器（如图M－9②）.实践探究：设小正方形纸板的边长为x cm，无盖长方体容器的容积为y cm3．
（1）求y与x之间的表达式；（2）若剪去的四个小正方形的边长为2 cm，则求该容器的容积．
解：（1）y＝（50－2x）（30－2x）x＝4x3－160x2＋1 500x．
（2）当x＝2时，y＝4×23－160×22＋1 500×2＝2 392．∴若剪去的四个小正方形的边长为2 cm，则该容器的容积为2 392 cm3.
五、解答题(三)(本大题共2小题，每小题12分，共24分)22. 综合探究问题情境：将下列完全平方式进行因式分解，将结果直接写在横线上．x2＋2x＋1＝（x＋1）2；4x2－4x＋1＝（2x－1）2；9x2－30x＋25＝__________________；
探究发现：观察以上多项式，发现：22＝4×1×1；（－4）2＝4×4×1；（－30）2＝4×9×25；归纳猜想：若多项式ax2＋bx＋c（a＞0，c＞0）是完全平方式，则a，b，c之间存在的数量关系为b2＝4ac；验证结论：嘉琪验证归纳猜想中的结论的过程如下，请补全嘉琪的验证过程；
解决问题：①若多项式（n＋1）x2－（2n＋6）x＋（n＋6）是一个完全平方式，求n的值；②若多项式9y2＋4加上一个含字母y的单项式就能变形为一个完全平方式，请直接写出所有满足条件的单项式．
解：①∵多项式（n＋1）x2－（2n＋6）x＋（n＋6）是一个完全平方式，∴[－（2n＋6）]2＝4（n＋1）（n＋6）.解得n＝3.
23. 综合运用数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．
（1）发现问题：如图M－10①，在△ABC和△AEF中，AB＝AC，AE＝AF，∠BAC＝∠EAF＝30°，连接BE，CF，延长BE交CF于点D,则BE与CF的数量关系：__________，∠BDC＝__________°；
（2）类比探究：如图M－10②，在△ABC和△AEF中，AB＝AC，AE＝AF，∠BAC＝∠EAF＝120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；（3）综合运用：如图M－10③，△ABC和△AEF都是等腰直角三角形，∠BAC＝∠EAF＝90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．求BF，CF，AM之间的数量关系，并说明理由.