数学八年级上册11.2.1 三角形的内角作业ppt课件

这是一份数学八年级上册11.2.1 三角形的内角作业ppt课件，共12页。

【A组】(基础过关)1．在Rt△ABC中，∠C＝90°，∠A＝2∠B，则∠A＝( )A. 30°B. 45°C. 60°D. 70°2. 若△ABC各内角的度数满足∠A＋∠B＝120°，∠C＝2∠A，则这个三角形是( )A. 锐角三角形B. 等边三角形C. 钝角三角形D. 直角三角形
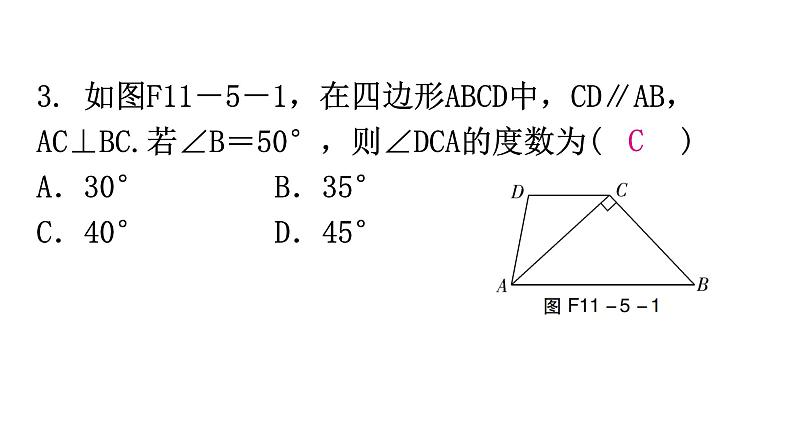
3. 如图F11－5－1，在四边形ABCD中，CD∥AB，AC⊥BC.若∠B＝50°，则∠DCA的度数为( )A．30°B．35°C．40°D．45°
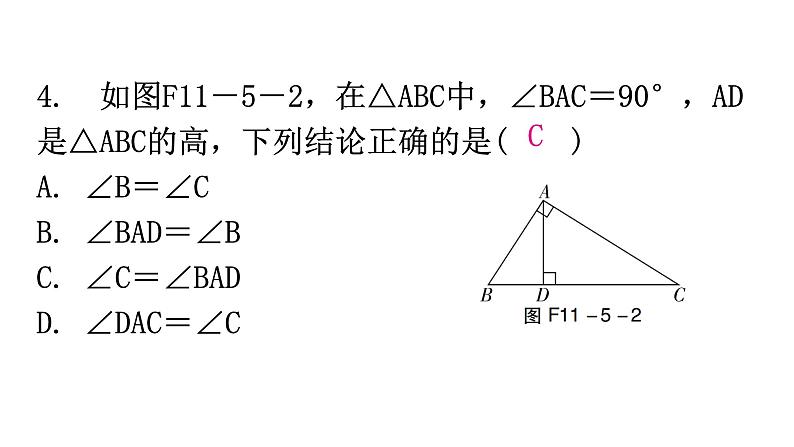
4. 如图F11－5－2，在△ABC中，∠BAC＝90°，AD是△ABC的高，下列结论正确的是( )A. ∠B＝∠CB. ∠BAD＝∠BC. ∠C＝∠BADD. ∠DAC＝∠C
5. 在直角三角形中，一个锐角等于另一个锐角的2倍，则较小的锐角的度数为______.
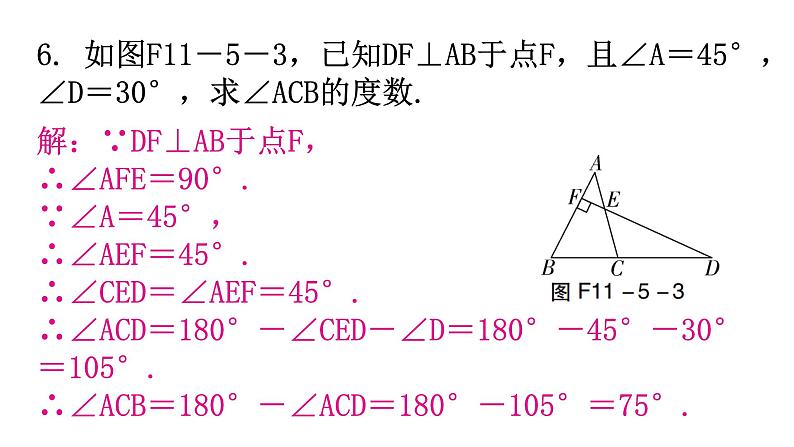
6. 如图F11－5－3，已知DF⊥AB于点F，且∠A＝45°，∠D＝30°，求∠ACB的度数.
解：∵DF⊥AB于点F，∴∠AFE＝90°.∵∠A＝45°，∴∠AEF＝45°.∴∠CED＝∠AEF＝45°.∴∠ACD＝180°－∠CED－∠D＝180°－45°－30°＝105°.∴∠ACB＝180°－∠ACD＝180°－105°＝75°.
【B组】(能力提升)7. 如图F11－5－4，AB，ED分别垂直于BD，点B，D是垂足，且∠ACB＝∠CED.求证：△ACE是直角三角形.
证明：∵AB⊥BD，ED⊥BD，∴∠ABC＝∠CDE＝90°.∴∠ACB＋∠BAC＝90°，∠CED＋∠DCE＝90°.又∵∠ACB＝∠CED，∴∠BAC＝∠DCE.∴∠ACB＋∠DCE＝90°.∴∠ACE＝180°－(∠ACB＋∠DCE)＝90°.∴△ACE是直角三角形.
8. (实践探究)如图F11－5－5，小明在计算机上用“几何画板”画了一个Rt△ABC，∠C＝90°，并画出了两锐角的角平分线AD，BE及其交点F.小明发现，无论怎样变动Rt△ABC的形状和大小，∠AFB的度数是定值.这个定值为______.
【C组】(探究拓展)9. 如图F11－5－6，在△ABC中，AD是角平分线，∠B＜∠C.(1)如图①，AE是高，∠B＝35°，∠C＝65°，求∠DAE的度数；(2)如图②，点E在AD上，EF⊥BC于F，试探究∠DEF与∠B，∠C的大小关系，并证明你的结论；
(3)如图③，点E在AD的延长线上，EF⊥BC于F，试探究∠DEF与∠B，∠C的大小关系是_________________________(直接写出结论，不需证明).