




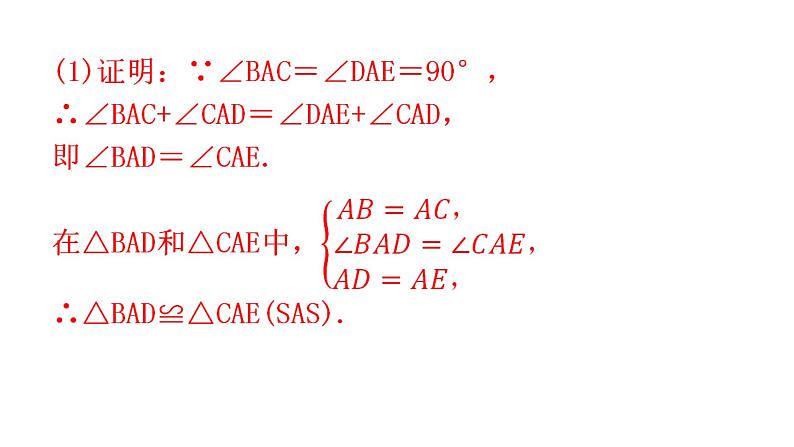

所属成套资源:全套人教版八年级数学上册专题教学课件
人教版八年级数学上册第十二章全等三角形专题六课标新导向教学课件
展开
这是一份人教版八年级数学上册第十二章全等三角形专题六课标新导向教学课件,共20页。
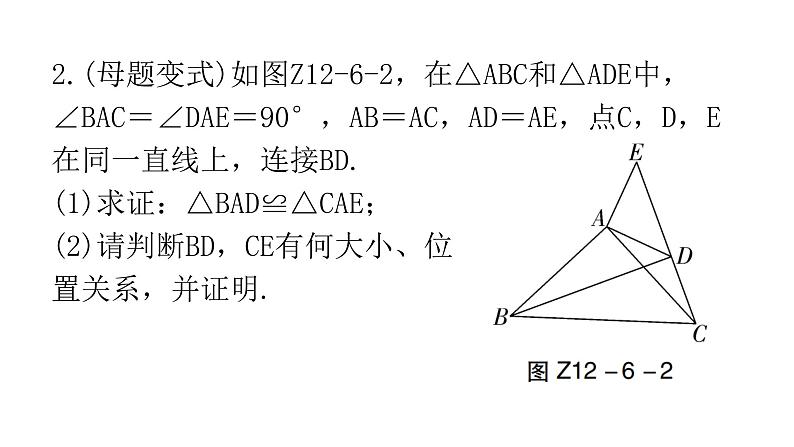
第十二章 全等三角形专题六 课标新导向01教材母题02跨学科融合03数学文化04实验探究1.(RJ八上P52改编)如图Z12-6-1,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF,EF与AD相交于点G.(1)求证:AE=AF;(2)求证:△AEG≌△AFG;(3)猜想:AD与EF的位置关系为__________,试证明你的猜想.互相垂直2.(母题变式)如图Z12-6-2,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一直线上,连接BD.(1)求证:△BAD≌△CAE;(2)请判断BD,CE有何大小、位置关系,并证明.3.(跨学科与地理融合)如图Z12-6-3,为测量湖两端AB的距离,某地理课外实践小组在湖旁的开阔地上选了一点C,测得∠ACB的度数,在AC的另一侧测得∠ACD=∠ACB,CD=CB,再测得AD的长,就是AB的长,那么判定△ABC≌△ADC的理由是( )A.SAS B.SSS C.ASA D.AASA4.(跨学科与物理融合)在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图Z12-6-4所示的方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,用a和b表示圆形容器的壁厚是__________.5.(几何与传统文化)莆仙戏是现存最古老的地方戏剧种之一,被称为“宋元南戏的活化石”,2021年5月莆仙戏《踏伞行》获评为“2020年度国家舞台艺术精品创作扶持工程重点扶持剧目”.该剧中“油纸伞”无疑是最重要的道具,依伞设戏,情节新颖,结构巧妙,谱写了一曲美轮美奂、诗意盎然的传统戏曲乐歌.“油纸伞”的制作工艺十分巧妙.如图Z12-6-5,伞圈D沿着伞柄滑动时,总有伞骨BD=CD,AB=AC,从而使得伞柄AP始终平分同一平面内两条伞骨所成的∠BAC.为什么?6.(几何与传统历史)风筝为中国人发明,相传墨翟以木头制成木鸟,研制三年有成,是人类最早的风筝起源.如图Z12-6-6,小飞在设计的“风筝”图案中,已知AB=AD,∠B=∠D,∠BAE=∠DAC,AC与AE相等吗?为什么?7.(实践探究)在学习完“探索三角形全等的条件”这一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:如图Z12-6-7,做一个“U”字形框架PABQ,其中AB=20 cm,AP,BQ足够长,PA⊥AB于点A,QB⊥AB于点B,点M从B出发向A运动,点N从B出发向Q运动,速度之比为2∶3,运动到某一瞬间两点同时停止,在AP上取点C,使△ACM与△BMN全等,求AC的长.解:设BM=2t cm,则BN=3t cm.∵PA⊥AB,QB⊥AB,∴∠A=∠B=90°.要使△ACM与△BMN全等,可分两种情况讨论:①当△BMN≌△ACM,即BM=AC,BN=AM时,∵BN=AM,AB=20 cm,∴3t=20-2t.解得t=4.∴AC=BM=2t=2×4=8(cm);②当△BMN≌△AMC,即BM=AM,BN=AC时,∵BM=AM,AB=20 cm,∴2t=20-2t.解得t=5.∴AC=BN=3t=3×5=15(cm).综上所述,AC的长为8 cm或15 cm.8.(实践探究)如图Z12-6-8,等边三角形ABC的边长为10 cm,点D在边AB上,且AD=4 cm,点P在线段BC上,以每秒2 cm的速度由点B向点C运动,同时点Q在线段CA上,由点C向点A运动.设点P运动时间为t s,若某一时刻△BPD与△CQP全等,求此时t的值及点Q的运动速度.解:由题意,得AD=4 cm,BD=6 cm,BP=2t cm,CP=(10-2t)cm.∵△ABC为等边三角形,∴∠B=∠C=60°.①当△BPD≌△CQP,即BP=CQ,BD=CP时,有CQ=2t,10-2t=6.解得t=2.∴CQ=4.∴点Q运动的速度为4÷2=2(cm/s);②当△BPD≌△CPQ,即BP=CP,BD=CQ时,有2t=10-2t,CQ=BD=6.解得t=2.5.∴点Q运动的速度为6÷2.5=2.4(cm/s).综上所述,当t=2时,点Q运动的速度为2 cm/s;当t=2.5时,点Q运动的速度为2.4 cm/s.






