人教版八年级数学上册第十三章轴对称专题四模型拓展——最值模型教学课件

这是一份人教版八年级数学上册第十三章轴对称专题四模型拓展——最值模型教学课件，共17页。
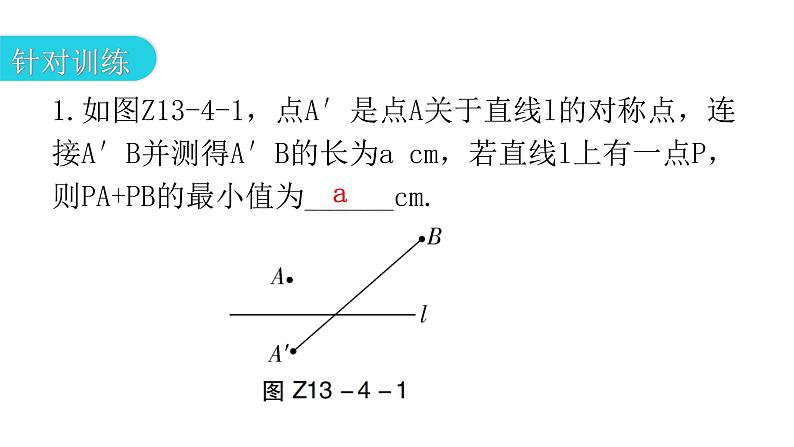
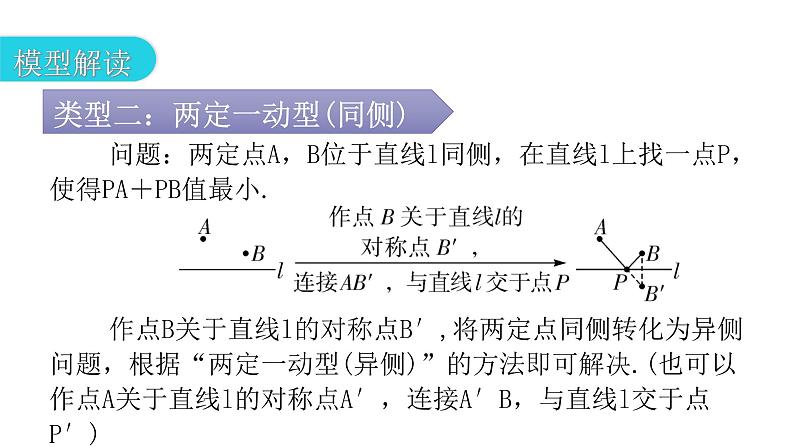
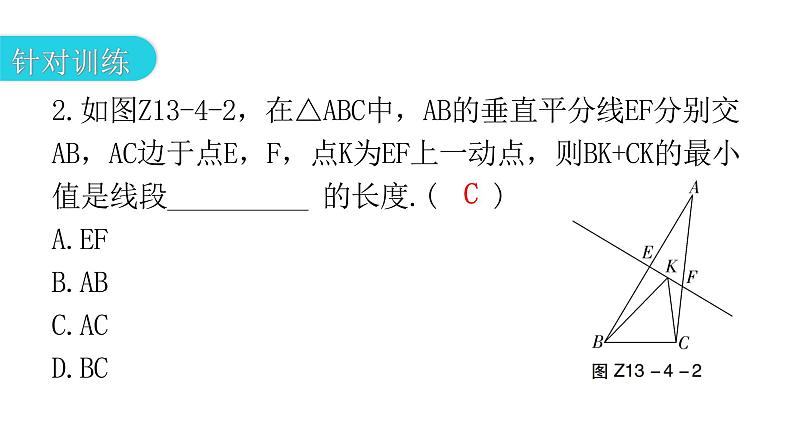
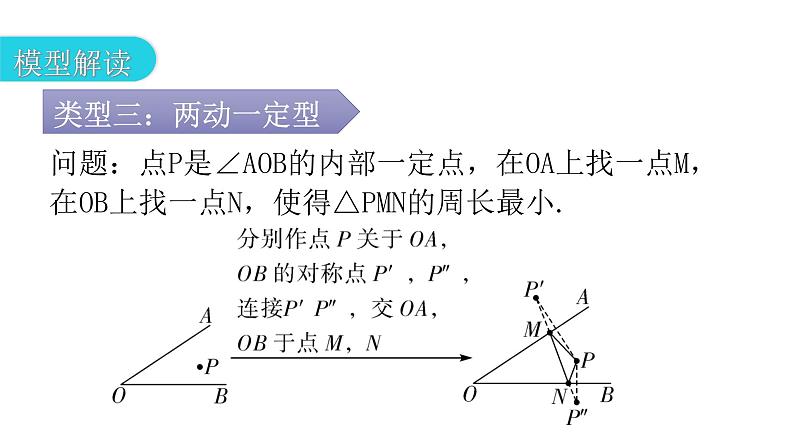
第十三章 轴对称专题四 模型拓展——最值模型01模型解读02针对训练1.如图Z13-4-1，点A′是点A关于直线l的对称点，连接A′B并测得A′B的长为a cm，若直线l上有一点P，则PA+PB的最小值为______cm.a 问题：两定点A，B位于直线l同侧，在直线l上找一点P，使得PA＋PB值最小. 作点B关于直线l的对称点B′,将两定点同侧转化为异侧问题，根据“两定一动型(异侧)”的方法即可解决.(也可以作点A关于直线l的对称点A′，连接A′B，与直线l交于点P′)2.如图Z13-4-2，在△ABC中，AB的垂直平分线EF分别交AB，AC边于点E，F，点K为EF上一动点，则BK+CK的最小值是线段__________ 的长度.( )A.EFB.ABC.ACD.BCC问题：点P是∠AOB的内部一定点，在OA上找一点M，在OB上找一点N，使得△PMN的周长最小. 作点P关于OA的对称点P′，再作点P关于OB的对称点P″.根据两点之间线段最短，将三条线段转化到同一直线P′P″上，即P′，M，N，P″四点共线时，PM＋PN＋MN＝P′P″取得最小值，此时△PMN的周长最小.3.如图Z13-4-3，∠AOB＝30°，M，N分别是射线OA，OB上的动点，OP平分∠AOB，且OP＝7 cm，则△PMN的周长的最小值为_______cm.7问题：点P,Q是∠AOB的内部两定点，在OA上找点M，在OB上找点N，使得四边形PQNM周长最小. 要使四边形PQNM周长最小，PQ为定值，即求得PM＋MN＋NQ的最小值即可，需将线段PM，MN，NQ三条线段尽可能转化到一条直线上，因此想到作点P关于OA的对称点P′，点Q关于OB的对称点Q′.当点P′,M,N,Q′四点共线时，PM＋MN＋NQ＝P′Q′取得最小值.4.如图Z13-4-4，牧马人从A地出发，先到草地边某一处牧马，再到河边饮马，然后回到B处，请画出最短路径.问题：已知l1∥l2，l1，l2之间距离为d，在l1，l2上分别找M，N两点，使得MN⊥l1，且AM＋MN＋NB的值最小. 要求AM＋MN＋NB的最小值，MN为定值，而点M,N分别是定长线段MN的两端点，故考虑平移点，构造平行四边形将AM,NB转化在同一条直线上.5.如图Z13-4-5，A，B两地在一条河的两岸，现要在河上建造一座桥MN.桥建造在何处才能使从A到B的路径AMNB最短？(假定河的两岸是平行的直线，桥要与河岸垂直)