
2023年江苏省镇江市中考数学真题(含解析)
展开镇江市2023年中考数学试卷
(满分:120分 考试时间:120分钟)
一、填空题(本大题共12小题,每小题2分,共24分)
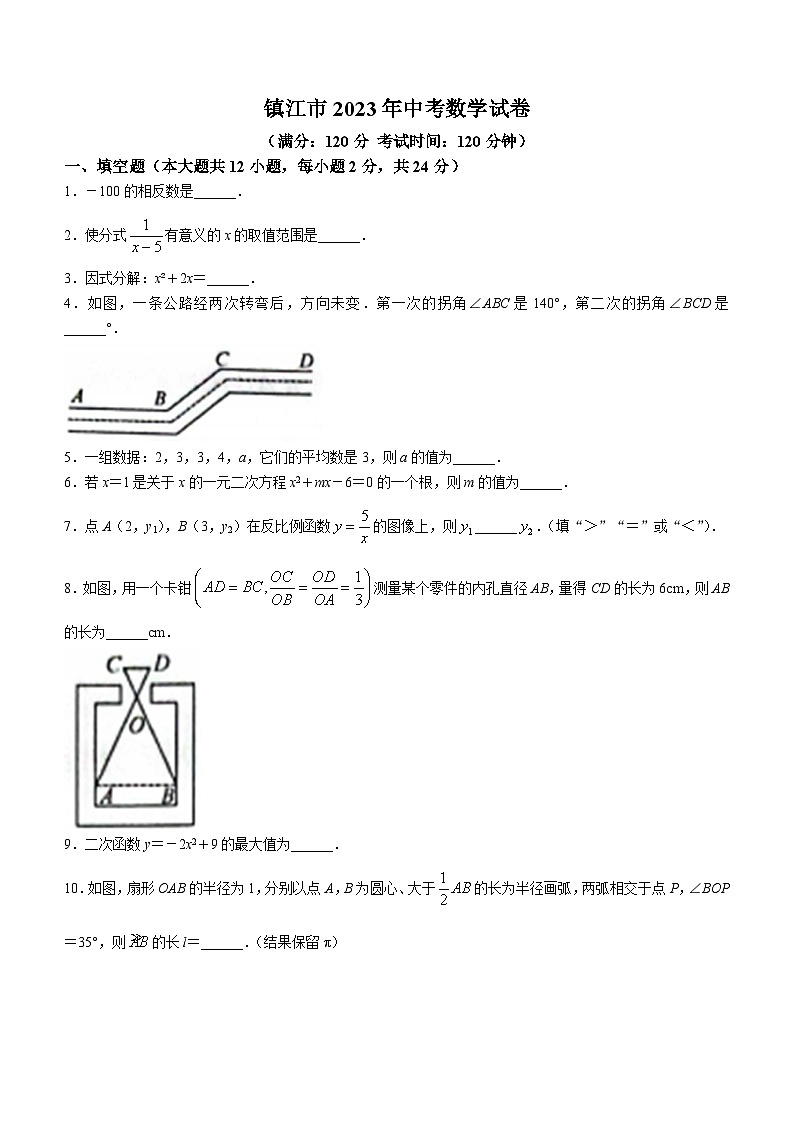
1.-100的相反数是______.
2.使分式有意义的x的取值范围是______.
3.因式分解:x²+2x=______.
4.如图,一条公路经两次转弯后,方向未变.第一次的拐角∠ABC是140°,第二次的拐角∠BCD是______°.
5.一组数据:2,3,3,4,a,它们的平均数是3,则a的值为______.
6.若x=1是关于x的一元二次方程x2+mx-6=0的一个根,则m的值为______.
7.点A(2,y1),B(3,y2)在反比例函数的图像上,则______.(填“>”“=”或“<”).
8.如图,用一个卡钳测量某个零件的内孔直径AB,量得CD的长为6cm,则AB的长为______cm.
9.二次函数y=-2x2+9的最大值为______.
10.如图,扇形OAB的半径为1,分别以点A,B为圆心、大于的长为半径画弧,两弧相交于点P,∠BOP=35°,则的长l=______.(结果保留π)
11.《九章算术》中记载:“今有勾八步,股一十五步.问勾中容圆,径几何?”译文:现在有一个直角三角形,短直角边的长为8步,长直角边的长为15步.问这个直角三角形内切圆的直径是多少?书中给出的算法译文如下:如图,根据短直角边的长和长直角边的长,求得斜边的长.用直角三角形三条边的长相加作为除数,用两条直角边相乘的积再乘2作为被除数,计算所得的商就是这个直角三角形内切圆的直径.根据以上方法,求得该直径等于______步.(注:“步”为长度单位)
12.已知一次函数y=kx+2的图像经过第一、二、四象限,以坐标原点O为圆心、r为半径作⊙O.若对于符合条件的任意实数k,一次函数y=kx+2的图像与⊙O总有两个公共点,则r的最小值为______.
二、选择题(本大题共6小题,每小题3分,共18分.在每小题所给出的四个选项中,恰有一项是符合题目要求的)
13.圆锥的侧面展开图是( )
A.三角形 B.菱形 C.扇形 D.五边形
14.下列运算中,结果正确的是( )
A.2m2+m2=3m4 B.m2·m4=m3 C.m4÷m2=m2 D.(m2)4=m6
15.据国家统计局公布,2023年第一季度,全国居民人均可支配收入10870元.数据10870用科学记数法表示为( )
A.1.087×104 B.10.87×104 C.10.87×103 D.1.087×103
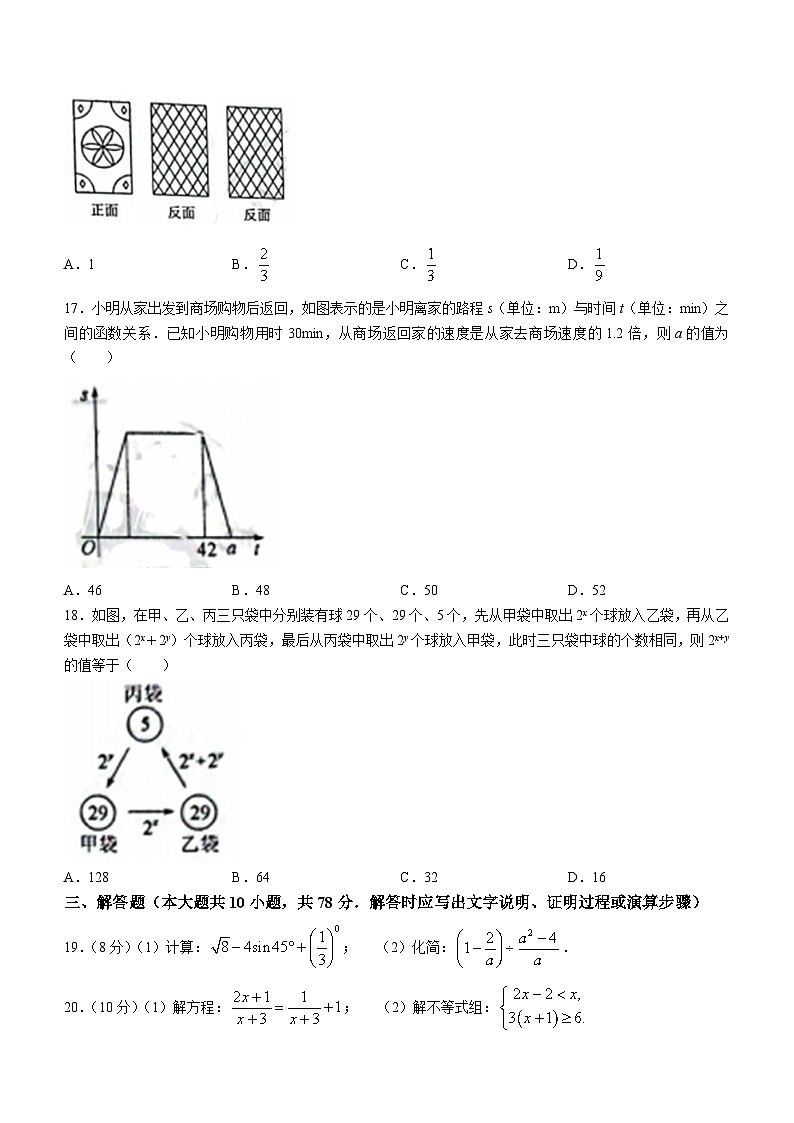
16.如图,桌面上有三张卡片,一张正面朝上.任意将其中一张卡片正反面对调一次,则这三张卡片中出现两张正面朝上的概率是( )
A.1 B. C. D.
17.小明从家出发到商场购物后返回,如图表示的是小明离家的路程s(单位:m)与时间t(单位:min)之间的函数关系.已知小明购物用时30min,从商场返回家的速度是从家去商场速度的1.2倍,则a的值为( )
A.46 B.48 C.50 D.52
18.如图,在甲、乙、丙三只袋中分别装有球29个、29个、5个,先从甲袋中取出2x个球放入乙袋,再从乙袋中取出(2x+2y)个球放入丙袋,最后从丙袋中取出2y个球放入甲袋,此时三只袋中球的个数相同,则2x+y的值等于( )
A.128 B.64 C.32 D.16
三、解答题(本大题共10小题,共78分.解答时应写出文字说明、证明过程或演算步骤)
19.(8分)(1)计算:; (2)化简:.
20.(10分)(1)解方程:; (2)解不等式组:
21.(6分)如图,B是AC的中点,点D,E在AC同侧,AE=BD,BE=CD.
(1)求证:△ABE≌△BCD.
(2)连接DE,求证:四边形BCDE是平行四边形.
22.(6分)一只不透明的袋子中装有2个红球和1个白球,这些球除颜色外都相同.将球搅匀,从中任意摸出1个球后,不放回,将袋中剩余的球搅匀,再从中任意摸出1个球.用列表或画树状图的方法,求两次都摸到红球的概率.
23.(6分)香醋中有一种物质,其含量不同,风味就不同,各风味香醋中该种物质的含量如下表.
风味 | 偏甜 | 适中 | 偏酸 |
含量/(mg/100mL) | 71.2 | 89.8 | 110.9 |
某超市销售不同包装(塑料瓶装和玻璃瓶装)的以上三种风味的香醋,小明将该超市1-5月份售出的香醋数量绘制成如下条形统计图.
已知1-5月份共售出150瓶香醋,其中“偏酸”的香醋占40%.
(1)求出a,b的值.
(2)售出的玻璃瓶装香醋中该种物质的含量的众数为______mg/100mL,中位数为______mg/100mL.
(3)根据小明绘制的条形统计图,你能获得哪些信息?(写出一条即可)
24.(6分)如图,正比例函数y=-3x与反比例函数的图像交于A,B(1,m)两点,点C在x轴负半轴上,∠ACO=45°.
(1)m=______,k=______,点C的坐标为______.
(2)点P在x轴上,若以B,O,P为顶点的三角形与△AOC相似,求点P的坐标.
25.(6分)如图,将矩形ABCD(AD>AB)沿对角线BD翻折,C的对应点为点,以矩形ABCD的顶点A为圆心、r为半径画圆,⊙A与相切于点E,延长DA交⊙A于点F,连接EF交AB于点G.
(1)求证:BE=BG.
(2)当r=1,AB=2时,求BC的长.
26.(8分)小磊安装了一个连杆装置,他将两根定长的金属杆各自的一个端点固定在一起,形成的角大小可变,将两杆各自的另一个端点分别固定在门框和门的顶部.
如图1是俯视图,OA,OB分别表示门框和门所在位置,M,N分别是OA,OB上的定点,OM=27cm,ON=36cm,MF,NF的长度固定,∠MFN的大小可变.
图1 图2 图3
(1)图2是门完全打开时的俯视图,此时,OA⊥OB,∠MFN=180°,求∠MNB的度数.
(2)图1中的门在开合过程中的某一时刻,点F的位置如图3所示,请在图3中作出此时门的位置OB.(用无刻度的直尺和圆规作图,不写作法,保留作图痕迹)
(3)在门开合的过程中,sin∠ONM的最大值为______.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
27.(11分)已知,在平面直角坐标系xOy中,点A的坐标为(3,0),点B的坐标为(m,n),点C与点B关于原点对称,直线AB,AC分别与y轴交于点E,F,点F在点E的上方,EF=2.
(1)分别求点E,F的纵坐标(用含m,n的代数式表示),并写出m的取值范围.
(2)求点B的横坐标m,纵坐标n之间的数量关系.(用含m的代数式表示n)
(3)将线段EF绕点(0,1)顺时针旋转90°,E,F的对应点分别是,.当线段与点B所在的某个函数图像有公共点时,求m的取值范围.
28.(11分)【发现】如图1,有一张三角形纸片ABC,小宏做如下操作:
图1 图2 图3
(1)取AB,AC的中点D,E,在边BC上作MN=DE;
(2)连接EM,分别过点D,N作DG⊥EM,NH⊥EM,垂足为G,H;
(3)将四边形BDGM剪下,绕点D旋转180°至四边形ADPQ的位置,将四边形CEHN剪下,绕点E旋转180°至四边形AEST的位置;
(4)延长PQ,ST交于点F.
小宏发现并证明了以下几个结论是正确的:
①点Q,A,T在一条直线上;
②四边形FPGS是矩形;
③△FQT≌△HMN;
④四边形FPGS与△ABC的面积相等.
【任务1】请你对结论①进行证明.
【任务2】如图2,在四边形ABCD中,,P,Q分别是AB,CD的中点,连接PQ.
求证:.
【任务3】如图3,有一张四边形纸片ABCD,,AD=2,BC=8,CD=9,,小丽分别取AB,CD的中点P,Q,在边BC上作MN=PQ,连接MQ,她仿照小宏的操作,将四边形ABCD分割、拼成了矩形.若她拼成的矩形恰好是正方形,求BM的长.
镇江市2023年中考数学参考答案
1.100 解析:本题考查了相反数的概念.只有符号不同的两个数互为相反数,∴100的相反数是-100.
2.x≠5 解析:本题考查了分式有意义的条件.根据题意,得x-5≠0,解得x≠5.
3.x(x+2) 解析:本题考查了用提公因式法进行因式分解.x2+2x=x(x+2).
4.140 解析:本题考查了平行线的性质.∵一条公路经两次转弯后,方向未变,∴转弯前后两条道路平行,∴∠BCD=∠ABC=140°(两直线平行,内错角相等).
5.3 解析:本题考查了算术平均数的计算.∵数据2,3,3,4,a的平均数是3,∴,解得a=3.
6.5 解析:本题考查了一元二次方程的解.能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.把x=1代入方程x2+mx-6=0,得1+m-6=0,解得m=5.
7.> 解析:本题考查了反比例函数图像上点的坐标特征、反比例函数的性质.在反比例函数中,k=5>0,∴该函数图像在第一、三象限,且在每一个象限内,y随x的增大而减小.又∵0<2<3,∴y1>y2.
8.18 解析:本题考查了对顶角的性质、相似三角形的实际应用.由对顶角相等得∠COD=∠AOB,又∵,∴,∴,∴.
9.9 解析:本题考查了二次函数的最值.根据二次函数的顶点式确定二次函数的最大值.∵二次函数的表达式为y=-2x2+9,∴当x=0时,二次函数取得最大值,为9.
10. 解析:本题考查了角平分线的作法与弧长的计算公式.解答本题的关键是能根据作图痕迹正确判断出OP是角平分线,并熟记弧长计算公式.由题意知,OP是∠AOB的平分线,∴∠AOB=2∠BOP=2×35°=70°,∴的长.
11.6 解析:本题考查了三角形的内切圆与内切圆直径的计算公式.根据勾股定理得,斜边的长为(步).由题中方法可得,该直角三角形内切圆的直径(步).
12.2 解析:本题考查了一次函数和几何问题的综合应用.∵y=kx+2的图像经过第一、二、四象限,∴k<0.由于y=kx+2过定点(0,2),当圆经过(0,2)时,由于直线呈下降趋势,因此必然与圆有另一个交点,∴r的临界点是2,∴r的最小值是2.
13.C 解析:本题考查了圆锥的侧面展开图.圆锥的侧面展开图是扇形.
14.C 解析:本题考查了合并同类项、同底数幂的乘法运算和除法运算、幂的乘方运算.2m2+m2=3m2,故A选项错误;,故B选项错误;,故C选项正确;,故D选项错误.
15.A 解析:本题考查了科学记数法.用科学记数法表示较大的数的一般形式为a×10n,其中1≤|a|<10,n等于原数的整数位数减1,∴10870=1.087×104.
16.B 解析:本题考查了概率的计算.任意将其中一张卡片正反面对调一次,共有3种情况:对调正面朝上的一张,三张正面都朝下,有1种情况;对调反面朝上的一张,有两张正面朝上,有2种情况.∴P(两张正面朝上).
17.D 解析:本题考查了一次函数的图像、一元一次方程的实际应用.根据“从家去商场和从商场返回家路程不变”列方程求解即可.设小明从家去商场的速度为xm/min,则他从商场返回家的速度为1.2xm/min.根据题意,得(42-30)x=(a-42)×1.2x,解得a=52.
18.A 解析:本题考查了幂的混合运算.找准数量关系,合理利用整体思想是解答本题的关键.调整后,甲袋中有(29-2x+2y)个球,乙袋中有(29-2y)个球,丙袋中有(5+2x)个球.∵一共有29+29+5=63(个)球,且调整后三只袋中球的个数相同,∴调整后每只袋中有63÷3=21(个)球,∴5+2x=21,29-2y=21,∴,,∴.
19.解析:本题考查了实数的混合运算、分式的混合运算.(1)先将算术平方根、特殊角的三角函数、零指数幂化简,然后计算可得答案;(2)先通分算出括号内的结果,再将除数中的分子进行因式分解,同时将除法运算转化为乘法运算,最后约分即可得到结果.
解:(1)原式.
(2)原式.
20.解析:本题考查了分式方程的解法、一元一次不等式组的解法.(1)先将方程两边同时乘(x+3)转化为整式方程,然后再根据整式方程的解法求解,最后注意要检验;(2)先分别求出两个不等式的解集,再找出这两个解集的公共部分即可得原不等式组的解集.
解:(1)方程两边同时乘(x+3),
得2x+1=1+x+3,解得x=3.
检验:当x=3时,x+3≠0,
∴x=3是原分式方程的解.
(2)解2x-2<x,得x<2;
解3(x+1)≥6,得x≥1.
∴原不等式组的解集是1≤x<2.
21.解析:本题考查了全等三角形的判定与性质、平行四边形的判定.(1)由B是AC的中点得AB=BC,结合AE=BD,BE=CD,根据全等三角形的判定定理“SSS”即可证明△ABE≌△BCD;(2)由(1)中△ABE≌△BCD得∠ABE=∠BCD,进一步得,再结合BE=CD,根据一组对边平行且相等的四边形是平行四边形即可证明.
证明:(1)∵B是AC的中点,∴AB=BC.
在△ABE和△BCD中,
∴△ABE≌△BCD(SSS).
(2)∵△ABE≌△BCD,∴∠ABE=∠BCD,∴.
又∵BE=CD,∴四边形BCDE是平行四边形.
22.解析:本题考查了用列表或画树状图的方法求概率.通过画树状图列举所有等可能的结果.再找出两次都摸到红球的结果,最后根据概率公式求解即可.
解:画树状图如图所示.
共有6种等可能的结果,其中两次都摸到红球的结果有2种,∴P(两次都摸到红球).
23.解析:本题考查了条形统计图、中位数和众数的定义.(1)由“偏酸”的香醋占总数的40%可求出两种包装“偏酸”风味香醋的总瓶数,用其减“玻璃瓶装”的瓶数即可求出a的值,用总瓶数150减条形统计图中其余所有频数即可得出b的值;(2)“玻璃瓶装”中频数最大的风味对应的浓度即为众数,把售出的三种风味对应的浓度数据由小到大排列,结合条形统计图中“玻璃瓶装”的频数求得的中间两个数据的平均数即为中位数;(3)根据题中表格和条形统计图,结合统计的意义回答即可.
解:(1)“偏酸”风味的瓶数为150×40%=60,∴a=60-42=18,
∴b=150-42-18-38-17-15=20.
(2)∵售出的玻璃瓶装香醋中“偏甜”风味的瓶数为20,“适中”风味的瓶数为38,“偏酸”风味的瓶数为42,
∴“偏酸”风味的香醋最多,∴众数为110.9mg/100mL;
∵共有20+38+42=100(个)数据,∴中位数为按从小到大排列后第50个数据和第51个数据的平均数,
∴中位数为.
故答案为110.9,89.8.
(3)答案合理即可.
24.解析:本题考查了反比例函数与一次函数的交点问题、相似三角形的性质.熟练掌握用待定系数法求函数表达式,并能利用数形结合思想和分类讨论思想分析是解答本题的关键.(1)点B是两函数图像的交点,利用待定系数法求出m,k的值;根据“A,B两点关于原点对称”求出点A的坐标,过点A作x轴的垂线,利用等腰直角三角形的性质,结合图形,求出点C的坐标.(2)根据点P在x轴上,结合图形,排除点P在x轴负半轴上的情形,当点P在x轴正半轴上时,两个三角形中已有一对角相等,而夹角的两边的对应关系不确定,故分类讨论:①△AOC∽△BOP;②△AOC∽△POB.分别求出两种情况下OP的长,从而得出点P的坐标.
解:(1)将B(1,m)代入y=-3x,得m=-3×1=-3,∴B(1,-3).
将B(1,-3)代入,得,∴k=-3.
如图,过点A作AD⊥x轴于点D,则∠ADC=90°.
∵点A,B关于原点O对称,∴A(-1,3),∴OD=1,AD=3.
又∵∠ACO=45°,∴CD=AD=3,∴OC=OD+CD=1+3=4,∴C(-4,0).
故答案为-3,-3,(-4,0).
(2)由(1)可知,B(1,-3),A(-1,3).
当点P在x轴的负半轴上时,
∠BOP>90°,∴∠BOP>∠AOC.
又∵∠BOP>∠ACO,∠BOP>∠CAO,
∴△BOP与△AOC不可能相似.
当点P在x轴的正半轴上时,∠AOC=∠BOP.
①若△AOC∽△BOP,则,
∵OA=OB,∴OP=OC=4,∴P(4,0);
②若△AOC∽△POB,则,
又∵,
∴,∴.
综上所述,点P的坐标为(4,0)或.
25.解析:本题是四边形与圆的综合题,考查了矩形、圆的切线、翻折的有关性质、锐角三角函数的定义,如何作辅助线,巧用解直角三角形是解答本题的关键.
(1)连接AE,由切线的性质得∠AEB=90°,则∠AEG+∠BEG=90°,由矩形的性质得∠BAD=∠BAF=90°,再由直角三角形两锐角互余得∠F+∠AGF=90°,根据对顶角相等和同圆的半径相等得∠BGE=∠AGF,∠F=∠AEG,然后由等角的余角相等得∠BGE=∠BEG,最后由等角对等边得出结论;(2)由锐角三角函数得,,得∠ABE=30°,由翻折得,由得∠CBD=30°,再由矩形对边相等得AB=CD,最后在Rt△BCD中解直角三角形即可得出结论.
(1)证明:如图,连接AE.∵⊙A与BC'相切于点E,∴∠AEB=90°,
∴∠AEG+∠BEG=90°.∵四边形ABCD是矩形,∴∠BAD=∠BAF=90°,
∴∠F+∠AGF=90°.∵AE=AF,∴∠F=∠AEG.
又∵∠BGE=∠AGF,∴∠BGE=∠BEG,∴BE=BG.
(2)解:在Rt△ABE中,AE=1,AB=2,
∴.∴∠ABE=30°.
∵四边形ABCD是矩形,∴∠ABC=90°.
由翻折可知,.
∵四边形ABCD是矩形,∴CD=AB=2.
在Rt△BCD中,,
∴.
26.解析:本题考查了旋转、尺规作图、锐角三角函数的有关知识.(1)在Rt△OMN中,利用锐角三角函数求得结果;(2)以点O为圆心、ON的长为半径画弧,与以点F为圆心、FN的长为半径的弧交于点N1,N2,连接ON1,ON2,得出门OB的位置;(3)当∠ONM最大时,sin∠ONM的值最大,过点O作MN的垂线段,当这条垂线段最大时,∠ONM最大,即当垂线段为OM即垂足为M时,∠ONM最大,故sin∠ONM的最大值为.
解:(1)在Rt△OMN中,,
∴∠ONM≈37°.∴∠MNB≈180°-37°=143°.
(2)门的位置OB如图1中OB1或OB2所示.(画出其中一条即可)
图1
(3)如图2,连接NM,过点O作OH⊥NM,交NM的延长线于点H.
∵在门的开合过程中,∠ONM在不断变化,
∴当∠ONM最大时,sin∠ONM的值最大.
由图2可知,当OH与OM重合时,OH取得最大值,此时∠ONM最大,
∴sin∠ONM的最大值为.
图2
27.解析:本题考查了用待定系数法求一次函数的表达式、一次函数图像上点的坐标特征、二次函数图像上点的坐标特征、旋转的性质.利用数形结合思想是解答本题的关键.(1)由对称的性质求出点C的坐标,设直线AB,AC的函数表达式,利用待定系数法即可求出与y轴的交点E,F的坐标;(2)点E,F都在y轴上,且点F在点E的上方,线段EF的长可用上边点的纵坐标减下边点的纵坐标表示,结合EF=2化简即可得m,n之间的数量关系;(3)由旋转得,点的纵坐标为1,由点在点B所在的函数图像上,求出点的横坐标,由线段与点B所在的函数图像有公共点,求出点横坐标与纵坐标的取值范围从而得出m的取值范围.
解:(1)由直线AB与y轴交于点E,得m≠3.
∵点C与点B关于原点对称,∴点C的坐标为(-m,-n).
由直线AC与y轴交于点F,得-m≠3,即m≠-3.综上所述,m≠±3.
设直线AB对应的一次函数表达式为y=kx+b,
将A(3,0),B(m,n)代入,得解得,
∴.同理可得,.
(2)由(1)得,.
又∵EF=2,点F在点E的上方,∴,
整理得.
(3)∵n与m的关系式为,
∴点B(m,n)在函数的图像上.
由旋转得,.
当点在点B所在的函数图像上时,,解得.
∵线段与点B所在的函数图像有公共点,
∴或.
由旋转得,或.
∵,
∴或.
28.解析:本题考查了旋转的性质、三角形的内角和定理、三点共线问题的证明、全等三角形的判定与性质、三角形的中位线定理、相似三角形的判定与性质、解直角三角形、勾股定理、梯形的面积计算.(1)由旋转的性质得对应角相等,即∠ABC=∠QAD,∠ACB=∠TAE,由三角形内角和定理得∠ABC+∠BAC+∠ACB=180°,从而得∠QAD+∠BAC+∠TAE=180°,即Q,A,T三点共线;(2)梯形中位线的证明问题常转化为三角形的中位线问题解决,连接AQ并延长,交BC的延长线于点E,证明△ADQ≌△ECQ,可得AQ=EQ,AD=CE,由三角形中位线定理得;(3)过点D作DR⊥BC于点R,由,得,从而得,由【发现】得,∴GE=6,PE=3,由【任务2】的结论得PQ=5,由勾股定理得EQ=4.过点Q作QH⊥BC,垂足为H.由及得,从而得,证明△PEQ∽△QHM,得,从而得.
【任务1】证法1:由旋转得,∠QAD=∠ABC,∠TAE=∠ACB.
在△ABC中,∠ABC+∠BAC+∠ACB=180°,
∴∠QAD+∠BAC+∠TAE=180°,
∴点Q,A,T在一条直线上.
证法2:由旋转得,∠QAD=∠ABC,∠TAE=∠ACB.
∴,.
∴点Q,A,T在一条直线上.
【任务2】证明:如图1,连接AQ并延长,交BC的延长线于点E.
∵,∴∠DAQ=∠E.∵Q是CD的中点,∴DQ=CQ.
在△ADQ和△ECQ中,
∴△ADQ≌△ECQ(AAS).∴AQ=EQ,AD=CE.
又∵P是AB的中点,
∴AP=BP,∴PQ是△ABE的中位线,
∴,∴.
图1
【任务3】解:用【发现】的方法画出示意图如图2所示.
图2
由【任务2】可得,.
过点D作DR⊥BC,垂足为R.
在Rt△DCR中,,
∴.
∴,
∴GE=6,PE=3.
在Rt△PEQ中,由勾股定理得.
过点Q作QH⊥BC,垂足为H.
∵Q是CD的中点,∴.
在Rt△QHC中,,
∴.
又由勾股定理得.
由,得∠PQE=∠QMH.
又∵∠PEQ=∠QHM=90°,∴△PEQ∽△QHM.
∴,即,∴.
∴.
2023年江苏省镇江市中考数学真题: 这是一份2023年江苏省镇江市中考数学真题,文件包含江苏省镇江市中考数学真题原卷版docx、江苏省镇江市中考数学真题解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
2020江苏省镇江市中考数学真题及答案: 这是一份2020江苏省镇江市中考数学真题及答案,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2019江苏省镇江市中考数学真题及答案: 这是一份2019江苏省镇江市中考数学真题及答案,共18页。试卷主要包含了填空题,选择题,解答题等内容,欢迎下载使用。












