人教版八年级上册14.1.4 整式的乘法课堂教学ppt课件

这是一份人教版八年级上册14.1.4 整式的乘法课堂教学ppt课件，共18页。PPT课件主要包含了知识回顾，教学目标，教学重难点，情景导入，引入新知，探究新知，应用新知，巩固新知，中考链接，课堂小结等内容，欢迎下载使用。

2.单项式与多项式相乘法则 3.单项式乘多项式转化为单项式乘单项式的依据是什么呢？体现了什么数学思想呢？
1.单项式与单项式相乘法则
1．理解多项式与多项式相乘的法则，并能运用法 则进行计算。2．理解算理，发展学生的运算能力和几何直观， 体会转化、数形结合和程序化思想。
1.重点：多项式乘法法则的形成过程以及理解和 应用 。 2.难点：探索多项式的乘法法则，灵活地进行整 式的乘法运算。
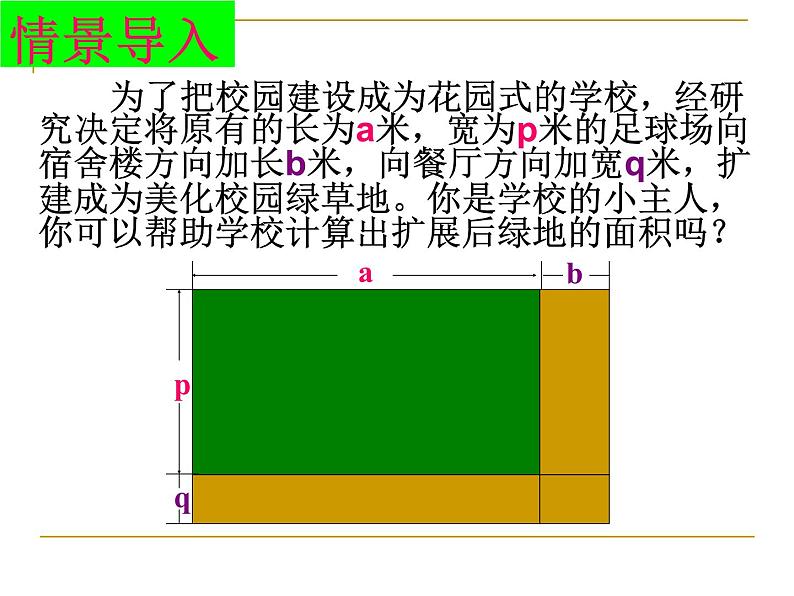
为了把校园建设成为花园式的学校，经研究决定将原有的长为a米，宽为p米的足球场向宿舍楼方向加长b米，向餐厅方向加宽q米，扩建成为美化校园绿草地。你是学校的小主人，你可以帮助学校计算出扩展后绿地的面积吗？
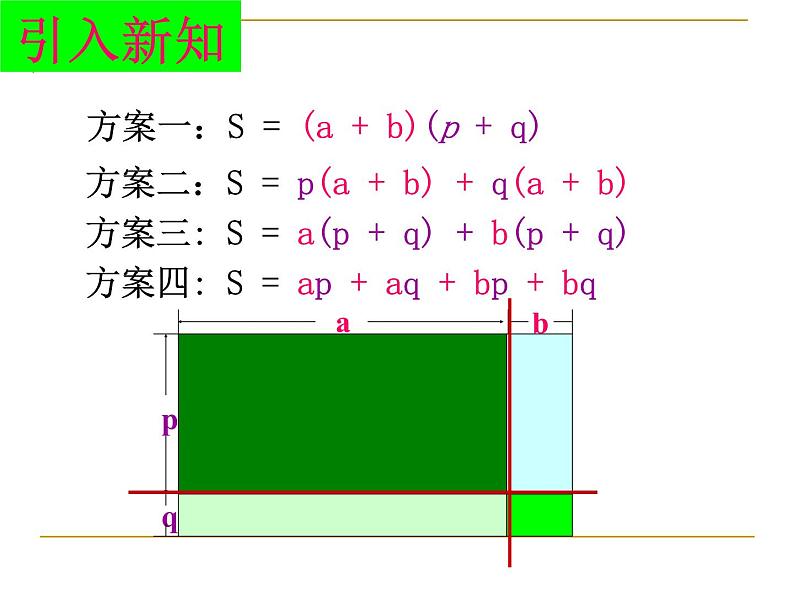
方案一：S = (a + b)(p + q)
方案二：S = p(a + b) + q(a + b)
方案三: S = a(p + q) + b(p + q)
方案四: S = ap + aq + bp + bq
∵四种方案算出的面积都相等；∴(a+b)(p+q)= p(a+b)+q(a+b) = ap+bp+aq+bq或(a+b)(p+q)= a(p+q)+b(p+q) = ap+aq+bp+bq
你能类比单项式与多项式相乘的法则，叙述出多项式与多项式相乘的法则吗？


多项式乘法法则: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。
即：(a+b)(p+q)=a(p+q)+b(p+q) =ap+aq+bp+bq


解：(1)原式 = 3x·x + 3x·(–2) + 1·x+1×(–2 )
例1. 计算：(1)( 3x + 1 )( x–2 ) ;(2)( x–8 y )( x–y ) .
= 3x² – 6x + x – 2
= 3x² – 5x – 2
（2）原式 = x·x + x·(–y) + (–8y)·x + (–8y)·(–y)
= x² - xy–8xy + 8y²
= x² - 9xy + 8y²
运用法则时要注意的事项：1.注意多项式中每一项都包括它前面的符号；2.运用法则时，要有序的逐项相乘，做到不重不漏；3.没有合并同类项之前，积的项数等于各个多项式项数的积；4.结果要合并同类项，化为最简形式。
1.计算： (1)(2x–3)(x+4) (2)(x+y)(x2–xy+y2)2.解方程:（x-2)(x-3）+18 =（x+1)(x+9)3.若使(x–q)(x2+px+2)的乘积中不含x2项， 则p与q的关系是( )A.互为倒数 B.互为相反数 C.相等 D.无法确定
已知:a+b=3，ab=﹣4，求(a－2)(b－2)的值.
（1）本节课你主要学习了哪些知识？（2）你体会到了哪些数学思想方法？（3）你又有哪些思想感悟与收获呢？

1.多项式乘法法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。
2.运用法则时，要有序的逐项相乘，做到不重不漏；注意多项式中每一项都包括它前面的符号；结果要合并同类项，化为最简形式。
在数学知识的学习中，“转化”思想是重要的思想方法。在今天的学习中，第一步是“转化”为单项式与多项式相乘，第二步是“转化”为单项式的乘法。即:将新的知识、方法化为已知的数学知识、方法。从而使学习能够顺利进行。
1.必做题: 课本第105页习题14.1复习巩固第5题；2.选做题：课本第106页习题14.1复习巩固第15题.
观察上面计算的结果，你能发现什么规律？
你能根据这个规律解决下面的问题吗？已知：（x + 2)(x + 6）= x² + mx + n ,试求：3m - 2n 的值 .
(x+p)(x+q)=x2+( )x+( )
你能根据这个规律解决下面的问题吗？已知：（x + 2)(x + 6）= x² + mx + n , 试求 ： 3m - 2n 的值.
(-1) (-6)
(-5) 6
(x+p)(x+q)=x2 +( )x+( )