2019年福建省中考数学试卷-(3年中考)

这是一份2019年福建省中考数学试卷-(3年中考)，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2017年福建省中考数学试卷-(3年中考)
一、选择题：本题共10小题，每小题4分，共40分．
1．3的相反数是（　　）
A．﹣3　　 B．﹣ 　　C． 　　D．3
2．如图，由四个正方体组成的几何体的左视图是（　　）
A． 　B． 　 C． 　D．
3．用科学记数法表示136 000，其结果是（　　）
A．0.136×106 　B．1.36×105 　C．136×103 　D．136×106
4．化简（2x）2的结果是（　　）
A．x4 B．2x2 C．4x2 D．4x
5．下列关于图形对称性的命题，正确的是（　　）
A．圆既是轴对称图形，又是中心对称图形　　　B．正三角形既是轴对称图形，又是中心对称图形
C．线段是轴对称图形，但不是中心对称图形　　D．菱形是中心对称图形，但不是轴对称图形
6．不等式组：的解集是（　　）
A．﹣3＜x≤2　 B．﹣3≤x＜2 　C．x≥2 　D．x＜﹣3
7．某校举行“汉字听写比赛”，5个班级代表队的正确答题数如图．这5个正确答题数所组成的一组数据的中位数和众数分别是（　　）
A．10，15 　B．13，15 　C．13，20 　D．15，15
　　　　　　　　
8．如图，AB是⊙O的直径，C，D是⊙O上位于AB异侧的两点．下列四个角中，一定与∠ACD互余的角是（　　）
A．∠ADC B．∠ABD C．∠BAC D．∠BAD
9．若直线y=kx+k+1经过点（m，n+3）和（m+1，2n﹣1），且0＜k＜2，则n的值可以是（　　）
A．3 B．4 C．5 D．6
10．如图，网格纸上正方形小格的边长为1．图中线段AB和点P绕着同一个点做相同的旋转，分别得到线段A'B'和点P'，则点P'所在的单位正方形区域是（　　）
A．1区 B．2区 C．3区 D．4区
二、填空题：本题共6小题，每小题4分，共24分．
11．计算|﹣2|﹣30=　 　．
12．如图，△ABC中，D，E分别是AB，AC的中点，连线DE．若DE=3，则线段BC的长等于　 　．
　　　　　　　　　
13．一个箱子装有除颜色外都相同的2个白球，2个黄球，1个红球．现添加同种型号的1个球，使得从中随机抽取1个球，这三种颜色的球被抽到的概率都是，那么添加的球是　 　．
14．已知A，B，C是数轴上的三个点，且C在B的右侧．点A，B表示的数分别是1，3，如图所示．若BC=2AB，则点C表示的数是　 　．
15．两个完全相同的正五边形都有一边在直线l上，且有一个公共顶点O，其摆放方式如图所示，则∠AOB等于　 　度．
16．已知矩形ABCD的四个顶点均在反比例函数y=的图象上，且点A的横坐标是2，则矩形ABCD的面积为　 　．
三、解答题：本题共9小题，共86分．
17．（8分）先化简，再求值：（1﹣）•，其中a=﹣1．







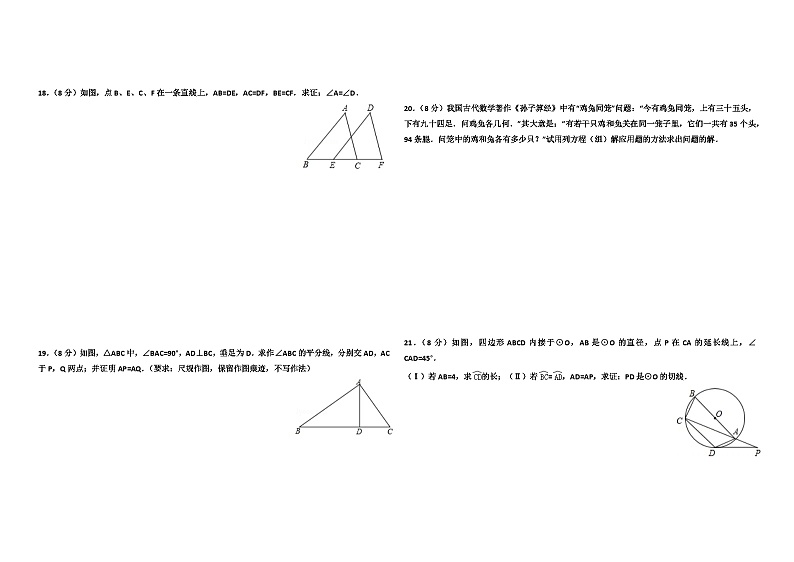
18．（8分）如图，点B、E、C、F在一条直线上，AB=DE，AC=DF，BE=CF．求证：∠A=∠D．












19．（8分）如图，△ABC中，∠BAC=90°，AD⊥BC，垂足为D．求作∠ABC的平分线，分别交AD，AC于P，Q两点；并证明AP=AQ．（要求：尺规作图，保留作图痕迹，不写作法）










20．（8分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足．问鸡兔各几何．”其大意是：“有若干只鸡和兔关在同一笼子里，它们一共有35个头，94条腿．问笼中的鸡和兔各有多少只？”试用列方程（组）解应用题的方法求出问题的解．












21．（8分）如图，四边形ABCD内接于⊙O，AB是⊙O的直径，点P在CA的延长线上，∠CAD=45°．
（Ⅰ）若AB=4，求的长；（Ⅱ）若=，AD=AP，求证：PD是⊙O的切线．









22．（10分）小明在某次作业中得到如下结果：
sin27°+sin283°≈0.122+0.992=0.9945，
sin222°+sin268°≈0.372+0.932=1.0018，
sin229°+sin261°≈0.482+0.872=0.9873，
sin237°+sin253°≈0.602+0.802=1.0000，
sin245°+sin245°≈（）2+（）2=1．
据此，小明猜想：对于任意锐角α，均有sin2α+sin2（90°﹣α）=1．
（Ⅰ）当α=30°时，验证sin2α+sin2（90°﹣α）=1是否成立；
（Ⅱ）小明的猜想是否成立？若成立，请给予证明；若不成立，请举出一个反例．





















23．（10分）自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车．某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费．具体收费标准如下：
使用次数
0
1
2
3
4
5（含5次以上）
累计车费
0
0.5
0.9
a
b
1.5
同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：
使用次数
0
1
2
3
4
5
人数
5
15
10
30
25
15
（Ⅰ）写出a，b的值；
（Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元．试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利？说明理由．

















24．（12分）如图，矩形ABCD中，AB=6，AD=8，P，E分别是线段AC、BC上的点，且四边形PEFD为矩形．
（Ⅰ）若△PCD是等腰三角形时，求AP的长；
（Ⅱ）若AP=，求CF的长．























25．（14分）已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M（1，0），且a＜b．
（Ⅰ）求抛物线顶点Q的坐标（用含a的代数式表示）；
（Ⅱ）说明直线与抛物线有两个交点；
（Ⅲ）直线与抛物线的另一个交点记为N．
（ⅰ）若﹣1≤a≤﹣，求线段MN长度的取值范围；
（ⅱ）求△QMN面积的最小值．
　
2017年福建省中考数学试卷答案
1． A．2． B．3． B．4． C．5． A．6． A．7． D．8． D．9． C．10． D．
11． 1．12． 6．13．红球．14． 7．　15． 108．16． ．
17．解：当a=﹣1时
原式=•
=
=
18．证明：∵BE=DF，
∴BC=EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SSS）．
∴∠A=∠D．
19．解：BQ就是所求的∠ABC的平分线，P、Q就是所求作的点．
证明：∵AD⊥BC，
∴∠ADB=90°，
∴∠BPD+∠PBD=90°．
∵∠BAC=90°，
∴∠AQP+∠ABQ=90°．
∵∠ABQ=∠PBD，
∴∠BPD=∠AQP．
∵∠BPD=∠APQ，
∴∠APQ=∠AQP，
∴AP=AQ．

20．解：设鸡有x只，兔有y只，鸡有一个头，两只脚，兔有1个头，四只脚，
结合上有三十五头，下有九十四足可得：，
解得：．
答：鸡有23只，兔有12只．
21．解：（Ⅰ）连接OC，OD，
∵∠COD=2∠CAD，∠CAD=45°，
∴∠COD=90°，
∵AB=4，
∴OC=AB=2，
∴的长=×π×2=π；
（Ⅱ）∵=，
∴∠BOC=∠AOD，
∵∠COD=90°，
∴∠AOD=45°，
∵OA=OD，
∴∠ODA=∠OAD，
∵∠AOD+∠ODA=∠OAD=180°，
∴∠ODA=67.5°，
∵AD=AP，
∴∠ADP=∠APD，
∵∠CAD=∠ADP+∠APD，∠CAD=45°，
∴∠ADP=CAD=22.5°，
∴∠ODP=∠ODA+∠ADP=90°，
∴PD是⊙O的切线．

22．解1：（1）当α=30°时，
sin2α+sin2（90°﹣α）
=sin230°+sin260°
=（）2+（）2
=+
=1；
（2）小明的猜想成立，证明如下：
如图，在△ABC中，∠C=90°，

设∠A=α，则∠B=90°﹣α，
∴sin2α+sin2（90°﹣α）
=（）2+（）2
=
=
=1．
23．解：（Ⅰ）a=0.9+0.3=1.2，b=1.2+0.2=1.4；
（Ⅱ）根据用车意愿调查结果，抽取的100名师生每人每天使用A品牌共享单车的平均车费为：
×（0×5+0.5×15+0.9×10+1.2×30+1.4×25+1.5×15）=1.1（元），
所以估计5000名师生一天使用共享单车的费用为：5000×1.1=5500（元），
因为5500＜5800，
故收费调整后，此运营商在该校投放A品牌共享单车不能获利．
24．解：（Ⅰ）在矩形ABCD中，AB=6，AD=8，∠ADC=90°，
∴DC=AB=6，
∴AC==10，
要使△PCD是等腰三角形，
①当CPCD时，AP=AC﹣CP=10﹣6=4，
②当PD=PC时，∠PDC=∠PCD，
∵∠PCD+∠PAD=∠PDC+∠PDA=90°，
∴∠PAD=∠PDA，
∴PD=PA，
∴PA=PC，
∴AP=AC=5，
③当DP=DC时，如图1，过点D作DQ⊥AC于Q，则PQ=CQ，
∵S△ADC=AD•DC=AC•DQ，
∴DQ==，
∴CQ==，
∴PC=2CQ=，
∴AP=AC﹣PC=10﹣=；
所以，若△PCD是等腰三角形时，AP=4或5或；
（Ⅱ）方法1、如图2，连接PF，DE，记PF与DE的交点为O，连接OC，
∵四边形ABCD和PEFD是矩形，
∴∠ADC=∠PDF=90°，
∴∠ADP+∠PDC=∠PDC+∠CDF，
∴∠ADP=∠CDF，
∵∠BCD=90°，OE=OD，
∴OC=ED，
在矩形PEFD中，PF=DE，
∴OC=PF，
∵OP=OF=PF，
∴OC=OP=OF，
∴∠OCF=∠OFC，∠OCP=∠OPC，
∵∠OPC+∠OFC+∠PCF=180°，
∴2∠OCP+2∠OCF=180°，
∴∠PCF=90°，
∴∠PCD+∠FCD=90°，
在Rt△ADC中，∠PCD+∠PAD=90°，
∴∠PAD=∠FCD，
∴△ADP∽△CDF，
∴，
∵AP=，
∴CF=．
方法2、如图，

∵四边形ABCD和DPEF是矩形，
∴∠ADC=∠PDF=90°，
∴∠ADP=∠CDF，
∵∠DGF+∠CDF=90°，
∴∠EGC+∠CDF=90°，
∵∠CEF+∠CGE=90°，
∴∠CDF=∠FEC，
∴点E，C，F，D四点共圆，
∵四边形DPEF是矩形，
∴点P也在此圆上，
∵PE=DF，∴，
∴∠ACB=∠DCF，
∵AD∥BC，
∴∠ACB=∠DAP，
∴∠DAP=∠DCF，
∵∠ADP=∠CDF，
∴△ADP∽△CDF，
∴，
∵AP=，
∴CF=．

25．解：（Ⅰ）∵抛物线y=ax2+ax+b过点M（1，0），
∴a+a+b=0，即b=﹣2a，
∴y=ax2+ax+b=ax2+ax﹣2a=a（x+）2﹣，
∴抛物线顶点Q的坐标为（﹣，﹣）；
（Ⅱ）∵直线y=2x+m经过点M（1，0），
∴0=2×1+m，解得m=﹣2，
联立直线与抛物线解析式，消去y可得ax2+（a﹣2）x﹣2a+2=0（*）
∴△=（a﹣2）2﹣4a（﹣2a+2）=9a2﹣12a+4，
由（Ⅰ）知b=﹣2a，且a＜b，
∴a＜0，b＞0，
∴△＞0，
∴方程（*）有两个不相等的实数根，
∴直线与抛物线有两个交点；
（Ⅲ）联立直线与抛物线解析式，消去y可得ax2+（a﹣2）x﹣2a+2=0，即x2+（1﹣）x﹣2+=0，
∴（x﹣1）[x﹣（﹣2）]=0，解得x=1或x=﹣2，
∴N点坐标为（﹣2，﹣6），
（i）由勾股定理可得MN2=[（﹣2）﹣1]2+（﹣6）2=﹣+45=20（﹣）2，
∵﹣1≤a≤﹣，
∴﹣2≤≤﹣1，
∴MN2随的增大而减小，
∴当=﹣2时，MN2有最大值245，则MN有最大值7，
当=﹣1时，MN2有最小值125，则MN有最小值5，
∴线段MN长度的取值范围为5≤MN≤7；
（ii）如图，设抛物线对称轴交直线与点E，

∵抛物线对称轴为x=﹣，
∴E（﹣，﹣3），
∵M（1，0），N（﹣2，﹣6），且a＜0，设△QMN的面积为S，
∴S=S△QEN+S△QEM=|（﹣2）﹣1|•|﹣﹣（﹣3）|=﹣﹣，
∴27a2+（8S﹣54）a+24=0（*），
∵关于a的方程（*）有实数根，
∴△=（8S﹣54）2﹣4×27×24≥0，即（8S﹣54）2≥（36）2，
∵a＜0，
∴S=﹣﹣＞，
∴8S﹣54＞0，
∴8S﹣54≥36，即S≥+，
当S=+时，由方程（*）可得a=﹣满足题意，
∴当a=﹣，b=时，△QMN面积的最小值为+．



2018年福建省中考数学试卷
一、选择题（本题共10小题，每题3分，共40分）
1．在实数|﹣3|，﹣2，0，π中，最小的数是（　　）
A．|﹣3|　　 B．﹣2 　　　C．0 　　　D．π
2．某几何体的三视图如图所示，则该几何体是（　　）
A．圆柱 B．三棱柱 　　C．长方体　　　 D．四棱锥
　　　　　　　　　　　　
3．下列各组数中，能作为一个三角形三边边长的是（　　）
A．1，1，2　　　 B．1，2，4 　　　　C．2，3，4 　　D．2，3，5
4．一个n边形的内角和为360°，则n等于（　　）
A．3 　　B．4 　　C．5 　　D．6
5．如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，则∠ACE等于（　　）
A．15° 　　　B．30° 　　C．45° 　　D．60°
6．投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（　　）
A．两枚骰子向上一面的点数之和大于1　　　　　B．两枚骰子向上一面的点数之和等于1
C．两枚骰子向上一面的点数之和大于12　　　　　D．两枚骰子向上一面的点数之和等于12
7．已知m=+，则以下对m的估算正确的（　　）
A．2＜m＜3 B．3＜m＜4 C．4＜m＜5 D．5＜m＜6
8．我国古代数学著作《增删算法统宗》记载”绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托“其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺，竿长y尺，则符合题意的方程组是（　　）
A． B． C． D．
9．如图，AB是⊙O的直径，BC与⊙O相切于点B，AC交⊙O于点D，若∠ACB=50°，则∠BOD等于（　　）
A．40° 　　　B．50° 　　C．60° 　　　D．80°
10．已知关于x的一元二次方程（a+1）x2+2bx+（a+1）=0有两个相等的实数根，下列判断正确的是（　　）
A．1一定不是关于x的方程x2+bx+a=0的根　　　B．0一定不是关于x的方程x2+bx+a=0的根
C．1和﹣1都是关于x的方程x2+bx+a=0的根　　　D．1和﹣1不都是关于x的方程x2+bx+a=0的根
二、细心填一填（本大题共6小题，每小题4分，满分24分）
11．计算：（）0﹣1= 　　　 ．
12．某8种食品所含的热量值分别为：120，134，120，119，126，120，118，124，则这组数据的众数为 　　　　 ．
13．如图，Rt△ABC中，∠ACB=90°，AB=6，D是AB的中点，则CD= 　　　 ．
　　　　　　　　　　　　　
14．不等式组的解集为 　　　 ．
15．把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB=，则CD= 　　　 ．
16．如图，直线y=x+m与双曲线y=相交于A，B两点，BC∥x轴，AC∥y轴，则△ABC面积的最小值为 　　　　 ．
三、专心解一解（本大题共9小题，满分86分）
17．（8分）解方程组：．[来源:学,科,网]




18．（8分）如图，▱ABCD的对角线AC，BD相交于点O，EF过点O且与AD，BC分别相交于点E，F．求证：OE=OF．












19．（8分）先化简，再求值：（﹣1）÷，其中m=+1．













20．（8分）求证：相似三角形对应边上的中线之比等于相似比．
要求：①根据给出的△ABC及线段A'B′，∠A′（∠A′=∠A），以线段A′B′为一边，在给出的图形上用尺规作出△A'B′C′，使得△A'B′C′∽△ABC，不写作法，保留作图痕迹；[来源:学§科§网]
②在已有的图形上画出一组对应中线，并据此写出已知、求证和证明过程．










21．（8分）如图，在Rt△ABC中，∠C=90°，AB=10，AC=8．线段AD由线段AB绕点A按逆时针方向旋转90°得到，△EFG由△ABC沿CB方向平移得到，且直线EF过点D．
（1）求∠BDF的大小；（2）求CG的长．







22．（10分）甲、乙两家快递公司揽件员（揽收快件的员工）的日工资方案如下：
甲公司为“基本工资+揽件提成”，其中基本工资为70元/日，每揽收一件提成2元；
乙公司无基本工资，仅以揽件提成计算工资．若当日揽件数不超过40，每件提成4元；若当日搅件数超过40，超过部分每件多提成2元．
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图：

（1）现从今年四月份的30天中随机抽取1天，求这一天甲公司揽件员人均揽件数超过40（不含40）的概率；
（2）根据以上信息，以今年四月份的数据为依据，并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数，解决以下问题：
①估计甲公司各揽件员的日平均件数；
②小明拟到甲、乙两家公司中的一家应聘揽件员，如果仅从工资收入的角度考虑，请利用所学的统计知识帮他选择，井说明理由．











23．（10分）如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．
（1）若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；
（2）求矩形菜园ABCD面积的最大值．
























24．（12分）已知四边形ABCD是⊙O的内接四边形，AC是⊙O的直径，DE⊥AB，垂足为E．
（1）延长DE交⊙O于点F，延长DC，FB交于点P，如图1．求证：PC=PB；
（2）过点B作BC⊥AD，垂足为G，BG交DE于点H，且点O和点A都在DE的左侧，如图2．若AB=，DH=1，∠OHD=80°，求∠BDE的大小．






















25．（14分）已知抛物线y=ax2+bx+c过点A（0，2）．
（1）若点（﹣，0）也在该抛物线上，求a，b满足的关系式；
（2）若该抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为心，OA为半径的圆与拋物线的另两个交点为B，C，且△ABC有一个内角为60°．
①求抛物线的解析式；②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．

2018年福建省中考数学试卷答案
1． B．2． C．3． C．4． B．5． A．6． D．7． B．8． A．9． D．10． D．
11． 0．12． 120．13． 3．14． x＞2．15． ﹣1．16． 6．
17．解：，
②﹣①得：3x=9，
解得：x=3，
把x=3代入①得：y=﹣2，
则方程组的解为．
18．证明：∵四边形ABCD是平行四边形，
∴OA=OC，AD∥BC，
∴∠OAE=∠OCF，
在△OAE和△OCF中，
，
∴△AOE≌△COF（ASA），
∴OE=OF．
19．解：（﹣1）÷
=
=
=，
当m=+1时，原式=．
20．解：（1）如图所示，△A'B′C′即为所求；

（2）已知，如图，△ABC∽△A'B'C'，===k，D是AB的中点，D'是A'B'的中点，
求证：=k．

证明：∵D是AB的中点，D'是A'B'的中点，
∴AD=AB，A'D'=A'B'，
∴==，
∵△ABC∽△A'B'C'，
∴=，∠A'=∠A，
∵=，∠A'=∠A，[来源:学科网ZXXK]
∴△A'C'D'∽△ACD，
∴==k．
21．解：（1）∵线段AD是由线段AB绕点A按逆时针方向旋转90°得到，
∴∠DAB=90°，AD=AB=10，
∴∠ABD=45°，
∵△EFG是△ABC沿CB方向平移得到，
∴AB∥EF，
∴∠BDF=∠ABD=45°；
（2）由平移的性质得，AE∥CG，AB∥EF，
∴∠DEA=∠DFC=∠ABC，∠ADE+∠DAB=180°，
∵∠DAB=90°，
∴∠ADE=90°，
∵∠ACB=90°，
∴∠ADE=∠ACB，
∴△ADE∽△ACB，
∴，
∵AB=8，AB=AD=10，
∴AE=12.5，
由平移的性质得，CG=AE=12.5．
22．解：（1）因为今年四月份甲公司揽件员人均揽件数超过40的有4天，
所以甲公司揽件员人均揽件数超过40（不含40）的概率为=；
（2）①甲公司各揽件员的日平均件数为=39件；
②甲公司揽件员的日平均工资为70+39×2=148元，
乙公司揽件员的日平均工资为
=[40+]×4+×6=159.4元，
因为159.4＞148，
所以仅从工资收入的角度考虑，小明应到乙公司应聘．
23．解：（1）设AB=xm，则BC=（100﹣2x）m，
根据题意得x（100﹣2x）=450，解得x1=5，x2=45，
当x=5时，100﹣2x=90＞20，不合题意舍去；
当x=45时，100﹣2x=10，
答：AD的长为10m；
（2）设AD=xm，
∴S=x（100﹣x）=﹣（x﹣50）2+1250，
当a≥50时，则x=50时，S的最大值为1250；
当0＜a＜50时，则当0＜x≤a时，S随x的增大而增大，当x=a时，S的最大值为50a﹣a2，
综上所述，当a≥50时，S的最大值为1250；当0＜a＜50时，S的最大值为50a﹣a2．
24．解：（1）如图1，∵AC是⊙O的直径，
∴∠ABC=90°，
∵DE⊥AB，
∴∠DEA=90°，
∴∠DEA=∠ABC，
∴BC∥DF，
∴∠F=∠PBC，
∵四边形BCDF是圆内接四边形，
∴∠F+∠DCB=180°，
∵∠PCB+∠DCB=180°，
∴∠F=∠PCB，
∴∠PBC=∠PCB，
∴PC=PB；
（2）如图2，连接OD，∵AC是⊙O的直径，
∴∠ADC=90°，
∵BG⊥AD，
∴∠AGB=90°，
∴∠ADC=∠AGB，
∴BG∥DC，
∵BC∥DE，
∴四边形DHBC是平行四边形，
∴BC=DH=1，
在Rt△ABC中，AB=，tan∠ACB=，
∴∠ACB=60°，
∴BC=AC=OD，
∴DH=OD，
在等腰三角形DOH中，∠DOH=∠OHD=80°，
∴∠ODH=20°，
设DE交AC于N，
∵BC∥DE，
∴∠ONH=∠ACB=60°，
∴∠NOH=180°﹣（∠ONH+∠OHD）=40°，
∴∠DOC=∠DOH﹣∠NOH=40°，
∵OA=OD，∴∠OAD=∠DOC=20°，
∴∠CBD=∠OAD=20°，
∵BC∥DE，
∴∠BDE=∠CBD=20°．

25．解：（1）∵抛物线y=ax2+bx+c过点A（0，2），
∴c=2．
又∵点（﹣，0）也在该抛物线上，
∴a（﹣）2+b（﹣）+c=0，
∴2a﹣b+2=0（a≠0）．
（2）①∵当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0，
∴x1﹣x2＜0，y1﹣y2＜0，
∴当x＜0时，y随x的增大而增大；
同理：当x＞0时，y随x的增大而减小，
∴抛物线的对称轴为y轴，开口向下，
∴b=0．
∵OA为半径的圆与拋物线的另两个交点为B、C，
∴△ABC为等腰三角形，
又∵△ABC有一个内角为60°，
∴△ABC为等边三角形．
设线段BC与y轴交于点D，则BD=CD，且∠OCD=30°，
又∵OB=OC=OA=2，
∴CD=OC•cos30°=，OD=OC•sin30°=1．
不妨设点C在y轴右侧，则点C的坐标为（，﹣1）．
∵点C在抛物线上，且c=2，b=0，
∴3a+2=﹣1，∴a=﹣1，
∴抛物线的解析式为y=﹣x2+2．
②证明：由①可知，点M的坐标为（x1，﹣+2），点N的坐标为（x2，﹣+2）．
直线OM的解析式为y=k1x（k1≠0）．
∵O、M、N三点共线，
∴x1≠0，x2≠0，且=，
∴﹣x1+=﹣x2+，[来源:Z。xx。k.Com]∴x1﹣x2=﹣，
∴x1x2=﹣2，即x2=﹣，
∴点N的坐标为（﹣，﹣+2）．
设点N关于y轴的对称点为点N′，则点N′的坐标为（，﹣+2）．
∵点P是点O关于点A的对称点，
∴OP=2OA=4，
∴点P的坐标为（0，4）．
设直线PM的解析式为y=k2x+4，
∵点M的坐标为（x，﹣+2），
∴﹣+2=k2x1+4，
∴k2=﹣，
∴直线PM的解析式为y=﹣+4．
∵﹣•+4==﹣+2，
∴点N′在直线PM上，∴PA平分∠MPN．


2019年福建省中考数学试卷
一、选择题（每小题4分，共40分）
1．计算22+（﹣1）0的结果是（　　）
A．5 B．4 C．3 D．2
2．北京故宫的占地面积约为720000m2，将720000用科学记数法表示为（　　）
A．72×104 B．7.2×105 C．7.2×106 D．0.72×106
3．下列图形中，一定既是轴对称图形又是中心对称图形的是（　　）
A．等边三角形 B．直角三角形 C．平行四边形 D．正方形
4．如图是由一个长方体和一个球组成的几何体，它的主视图是（　　）
A．　　B．　　C．　　D．
5．已知正多边形的一个外角为36°，则该正多边形的边数为（　　）
A．12 B．10 C．8 D．6
6．如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图，则下列判断错误的是（　　）
A．甲的数学成绩高于班级平均分，且成绩比较稳定
B．乙的数学成绩在班级平均分附近波动，且比丙好
C．丙的数学成绩低于班级平均分，但成绩逐次提高
D．就甲、乙、丙三个人而言，乙的数学成绩最不稳
　　　　　　　　
7．下列运算正确的是（　　）
A．a•a3＝a3　　　　　B．（2a）3＝6a3 C．a6÷a3＝a2　　　　　D．（a2）3﹣（﹣a3）2＝0
8．《增删算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增添一倍多，问若每日读多少？”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍，问他每天各读多少个字？已知《孟子》一书共有34685个字，设他第一天读x个字，则下面所列方程正确的是（　　）
A．x+2x+4x＝34685　　B．x+2x+3x＝34685 　　C．x+2x+2x＝34685　　D．x+x+x＝34685
9．如图，PA、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB＝55°，则∠APB等于（　　）
A．55° B．70° C．110° D．125°
10．若二次函数y＝|a|x2+bx+c的图象经过A（m，n）、B（0，y1）、C（3﹣m，n）、D（，y2）、E（2，y3），则y1、y2、y3的大小关系是（　　）
A．y1＜y2＜y3 B．y1＜y3＜y2 C．y3＜y2＜y1 D．y2＜y3＜y1
二、填空题（每小题4分，共24分）
11．因式分解：x2﹣9＝　 　．
12．如图，数轴上A、B两点所表示的数分别是﹣4和2，点C是线段AB的中点，则点C所表示的数是　 　．
　　　　　　　　　　　　
13．某校征集校运会会徽，遴选出甲、乙、丙三种图案．为了解何种图案更受欢迎，随机调查了该校100名学生，其中60名同学喜欢甲图案，若该校共有2000人，根据所学的统计知识可以估计该校喜欢甲图案的学生有　 　人．
14．在平面直角坐标系xOy中，▱OABC的三个顶点O（0，0）、A（3，0）、B（4，2），则其第四个顶点是　 　．
15．如图，边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合，E、F分别是AD、BA的延长与⊙O的交点，则图中阴影部分的面积是　 　．（结果保留π）
16．如图，菱形ABCD顶点A在函数y＝（x＞0）的图象上，函数y＝（k＞3，x＞0）的图象关于直线AC对称，且经过点B、D两点，若AB＝2，∠BAD＝30°，则k＝　 　．
三、解答题（共86分）17．（8分）解方程组．




18．（8分）如图，点E、F分别是矩形ABCD的边AB、CD上的一点，且DF＝BE．求证：AF＝CE．














19．（8分）先化简，再求值：（x﹣1）÷（x﹣），其中x＝+1．












20．（8分）已知△ABC和点A'，如图．
（1）以点A'为一个顶点作△A'B'C'，使△A'B'C'∽△ABC，且△A'B'C'的面积等于△ABC面积的4倍；（要求：尺规作图，不写作法，保留作图痕迹）
（2）设D、E、F分别是△ABC三边AB、BC、AC的中点，D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、C'A'的中点，求证：△DEF∽△D'E'F'．









21．（8分）在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．
（1）当点E恰好在AC上时，如图1，求∠ADE的大小；
（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．







22．（10分）某工厂为贯彻落实“绿水青山就是金山银山“的发展理念，投资组建了日废水处理量为m吨的废水处理车间，对该厂工业废水进行无害化处理．但随着工厂生产规模的扩大，该车间经常无法完成当天工业废水的处理任务，需要将超出日废水处理量的废水交给第三方企业处理．已知该车间处理废水，每天需固定成本30元，并且每处理一吨废水还需其他费用8元；将废水交给第三方企业处理，每吨需支付12元．根据记录，5月21日，该厂产生工业废水35吨，共花费废水处理费370元．
（1）求该车间的日废水处理量m；
（2）为实现可持续发展，走绿色发展之路，工厂合理控制了生产规模，使得每天废水处理的平均费用不超过10元/吨，试计算该厂一天产生的工业废水量的范围．






















23．（10分）某种机器使用期为三年，买方在购进机器时，可以给各台机器分别一次性额外购买若干次维修服务，每次维修服务费为2000元．每台机器在使用期间，如果维修次数未超过购机时购买的维修服务次数，每次实际维修时还需向维修人员支付工时费500元；如果维修次数超过购机时购买的维修服务次数，超出部分每次维修时需支付维修服务费5000元，但无需支付工时费．某公司计划购买1台该种机器，为决策在购买机器时应同时一次性额外购买几次维修服务，搜集并整理了100台这种机器在三年使用期内的维修次数，整理得下表；
维修次数
8
9
10
11
12
频率（台数）
10
20
30
30
10
（1）以这100台机器为样本，估计“1台机器在三年使用期内维修次数不大于10”的概率；
（2）试以这100机器维修费用的平均数作为决策依据，说明购买1台该机器的同时应一次性额外购10次还是11次维修服务？




















24．（12分）如图，四边形ABCD内接于⊙O，AB＝AC，AC⊥BD，垂足为E，点F在BD的延长线上，且DF＝DC，连接AF、CF．
（1）求证：∠BAC＝2∠CAD；
（2）若AF＝10，BC＝4，求tan∠BAD的值．
























25．（14分）已知抛物y＝ax2+bx+c（b＜0）与x轴只有一个公共点．
（1）若抛物线与x轴的公共点坐标为（2，0），求a、c满足的关系式；
（2）设A为抛物线上的一定点，直线l：y＝kx+1﹣k与抛物线交于点B、C，直线BD垂直于直线y＝﹣1，垂足为点D．当k＝0时，直线l与抛物线的一个交点在y轴上，且△ABC为等腰直角三角形．
①求点A的坐标和抛物线的解析式；②证明：对于每个给定的实数k，都有A、D、C三点共线．
2019年福建省中考数学试卷答案
1． A．2． B．3． D．4． C．5． B．6． D．7． D．8． A．9． B．10． D．
11．（x+3）（x﹣3）．12．﹣113． 1200．14．（1，2）．15．π﹣1．16． 6+2．
17．解：，
①+②得：3x＝9，即x＝3，
把x＝3代入①得：y＝﹣2，
则方程组的解为．
18．证明：∵四边形ABCD是矩形，
∴∠D＝∠B＝90°，AD＝BC，
在△ADF和△BCE中，，
∴△ADF≌△BCE（SAS），
∴AF＝CE．
19．解：原式＝（x﹣1）÷
＝（x﹣1）•
＝，
当x＝+1，
原式＝
＝1+．
20．解：（1）作线段A'C'＝2AC、A'B'＝2AB、B'C'＝2BC，得△A'B'C'即可所求．

证明：∵A'C'＝2AC、A'B'＝2AB、B'C'＝2BC，
∴△ABC∽△A′B′C′，
∴
（2）证明：

∵D、E、F分别是△ABC三边AB、BC、AC的中点，
∴DE＝，，，
∴△DEF∽△ABC
同理：△D'E'F'∽△A'B'C'，
由（1）可知：△ABC∽△A′B′C′，
∴△DEF∽△D'E'F'．
21．（1）解：如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC上，
∴CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，
∵CA＝CD，
∴∠CAD＝∠CDA＝（180°﹣30°）＝75°，
∴∠ADE＝90°﹣75°＝25°；
（2）证明：如图2，
∵点F是边AC中点，
∴BF＝AC，
∵∠ACB＝30°，
∴AB＝AC，
∴BF＝AB，
∵△ABC绕点A顺时针旋转60得到△DEC，
∴∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，
∴DE＝BF，△ACD和△BCE为等边三角形，
∴BE＝CB，
∵点F为△ACD的边AC的中点，
∴DF⊥AC，
易证得△CFD≌△ABC，
∴DF＝BC，
∴DF＝BE，
而BF＝DE，
∴四边形BEDF是平行四边形．
22．解：（1）∵35×8+30＝310（元），310＜350，
∴m＜35．
依题意，得：30+8m+12（35﹣m）＝370，
解得：m＝20．
答：该车间的日废水处理量为20吨．
（2）设一天产生工业废水x吨，
当0＜x≤20时，8x+30≤10x，
解得：15≤x≤20；
当x＞20时，12（x﹣20）+8×20+30≤10x，
解得：20＜x≤25．
综上所述，该厂一天产生的工业废水量的范围为15≤x≤20．
23．解：（1）“1台机器在三年使用期内维修次数不大于10”的概率＝＝0.6．
（2）购买10次时，
某台机器使用期内维修次数
8
9
10
11
12
该台机器维修费用
24000
24500
25000
30000
35000
此时这100台机器维修费用的平均数
y1＝（24000×10+24500×20+25000×30+30000×30+35000×10）＝27300
购买11次时，
某台机器使用期内维修次数
8
9
10
11
12
该台机器维修费用
26000
26500
27000
27500
32500
此时这100台机器维修费用的平均数
y2＝（26000×10+26500×20+27000×30+27500×30+32500×10）＝27500，
∵27300＜27500，
所以，选择购买10次维修服务．
24．解：（1）∵AB＝AC，
∴＝，∠ABC＝∠ACB，
∴∠ABC＝∠ADB，∠ABC＝（180°﹣∠BAC）＝90°﹣∠BAC，
∵BD⊥AC，
∴∠ADB＝90°﹣∠CAD，
∴∠BAC＝∠CAD，
∴∠BAC＝2∠CAD；
（2）解：∵DF＝DC，
∴∠DFC＝∠DCF，
∴∠BDC＝2∠DFC，
∴∠BFC＝∠BDC＝∠BAC＝∠FBC，
∴CB＝CF，
又BD⊥AC，
∴AC是线段BF的中垂线，AB＝AF＝10，AC＝10．
又BC＝4，
设AE＝x，CE＝10﹣x，
由AB2﹣AE2＝BC2﹣CE2，得100﹣x2＝80﹣（10﹣x）2，
解得x＝6，
∴AE＝6，BE＝8，CE＝4，
∴DE＝＝＝3，
∴BD＝BE+DE＝3+8＝11，
作DH⊥AB，垂足为H，
∵AB•DH＝BD•AE，
∴DH＝＝＝，
∴BH＝＝，
∴AH＝AB﹣BH＝10﹣＝，
∴tan∠BAD＝＝＝．

25．解：（1）抛物线与x轴的公共点坐标即为函数顶点坐标，故：y＝a（x﹣2）2＝ax2﹣4ax+4a，
则c＝4a；
（2）y＝kx+1﹣k＝k（x﹣1）+1过定点（1，1），
且当k＝0时，直线l变为y＝1平行x轴，与轴的交点为（0，1），
又△ABC为等腰直角三角形，
∴点A为抛物线的顶点；
①c＝1，顶点A（1，0），
抛物线的解析式：y＝x2﹣2x+1，
②，

x2﹣（2+k）x+k＝0，
x＝（2+k±），
xD＝xB＝（2+k﹣），yD＝﹣1；
则D，
yC＝（2+k2+k，
C，A（1，0），
∴直线AD表达式中的k值为：kAD＝＝，
直线AC表达式中的k值为：kAC＝，
∴kAD＝kAC，点A、C、D三点共线．