2019年广东省深圳市中考数学试卷－（6年中考）

这是一份2019年广东省深圳市中考数学试卷－（6年中考），共28页。试卷主要包含了选择题，填空题，解答题　　17．0等内容，欢迎下载使用。
2019年广东省深圳市中考数学试卷-(6年中考)
一、选择题（每小题3分，共12小题，满分36分）
1．﹣的绝对值是（　　）
A．﹣5 B． C．5 D．﹣
2．下列图形中是轴对称图形的是（　　）
A． B． C． D．
3．预计到2025年，中国5G用户将超过460000000，将460000000用科学记数法表示为（　　）
A．4.6×109 B．46×107 C．4.6×108 D．0.46×109
4．下列哪个图形是正方体的展开图（　　）
A． 　　B．　　　C．　　D．
5．这组数据20，21，22，23，23的中位数和众数分别是（　　）
A．20，23 B．21，23 C．21，22 D．22，23
6．下列运算正确的是（　　）
A．a2+a2＝a4 B．a3•a4＝a12 C．（a3）4＝a12 D．（ab）2＝ab2
7．如图，已知l1∥AB，AC为角平分线，下列说法错误的是（　　）
A．∠1＝∠4 B．∠1＝∠5 C．∠2＝∠3 D．∠1＝∠3
　　　　　　　　　　　
8．如图，已知AB＝AC，AB＝5，BC＝3，以A，B两点为圆心，大于AB的长为半径画圆弧，两弧相交于点M，N，连接MN与AC相交于点D，则△BDC的周长为（　　）
A．8 B．10 C．11 D．13
9．已知y＝ax2+bx+c（a≠0）的图象如图，则y＝ax+b和y＝的图象为（　　）
A．B． C．D．
10．下面命题正确的是（　　）
A．矩形对角线互相垂直 B．方程x2＝14x的解为x＝14
C．六边形内角和为540° D．一条斜边和一条直角边分别相等的两个直角三角形全等
11．定义一种新运算n•xn﹣1dx＝an﹣bn，例如2xdx＝k2﹣n2，若﹣x﹣2dx＝﹣2，则m＝（　　）
A．﹣2 B．﹣ C．2 D．
12．已知菱形ABCD，E、F是动点，边长为4，BE＝AF，∠BAD＝120°，则下列结论正确的有几个（　　）
①△BEC≌△AFC；②△ECF为等边三角形；③∠AGE＝∠AFC；④若AF＝1，则＝．
A．1 B．2 C．3 D．4
二、填空题（每小题3分，共4小题，满分12分）
13．分解因式：ab2﹣a＝　 　．
14．现有8张同样的卡片，分别标有数字：1，1，2，2，2，3，4，5，将这些卡片放在一个不透明的盒子里，搅匀后从中随机地抽出一张，抽到标有数字2的卡片的概率是　 　．
15．如图，在正方形ABCD中，BE＝1，将BC沿CE翻折，使B点对应点刚好落在对角线AC上，将AD沿AF翻折，使D点对应点刚好落在对角线AC上，求EF＝　 　．
　　　　　　　　　　　
16．如图，在Rt△ABC中，∠ABC＝90°，C（0，﹣3），CD＝3AD，点A在反比例函数y＝图象上，且y轴平分∠ACB，求k＝　 　．
三、解答题　　17．（5分）计算：﹣2cos60°+（）﹣1+（π﹣3.14）0



18．（6分）先化简（1﹣）÷，再将x＝﹣1代入求值．











19．（7分）某校为了了解学生对中国民族乐器的喜爱情况，随机抽取了本校的部分学生进行调查（每名学生选择并且只能选择一种喜爱的乐器），现将收集到的数据绘制成如下两幅不完整的统计图．

（1）这次共抽取　 　名学生进行调查，扇形统计图中的x＝　 　；
（2）请补全统计图；
（3）在扇形统计图中“扬琴”所对扇形的圆心角是　 　度；
（4）若该校有3000名学生，请你佔计该校喜爱“二胡”的学生约有　 　名．







20．（8分）如图所示，某施工队要测量隧道长度BC，AD＝600米，AD⊥BC，施工队站在点D处看向B，测得仰角为45°，再由D走到E处测量，DE∥AC，ED＝500米，测得仰角为53°，求隧道BC长．（sin53°≈，cos53°≈，tan53°≈）．








21．（8分）有A、B两个发电厂，每焚烧一吨垃圾，A发电厂比B发电厂多发40度电，A焚烧20吨垃圾比B焚烧30吨垃圾少1800度电．
（1）求焚烧1吨垃圾，A和B各发电多少度？
（2）A、B两个发电厂共焚烧90吨的垃圾，A焚烧的垃圾不多于B焚烧的垃圾两倍，求A厂和B厂总发电量的最大值．












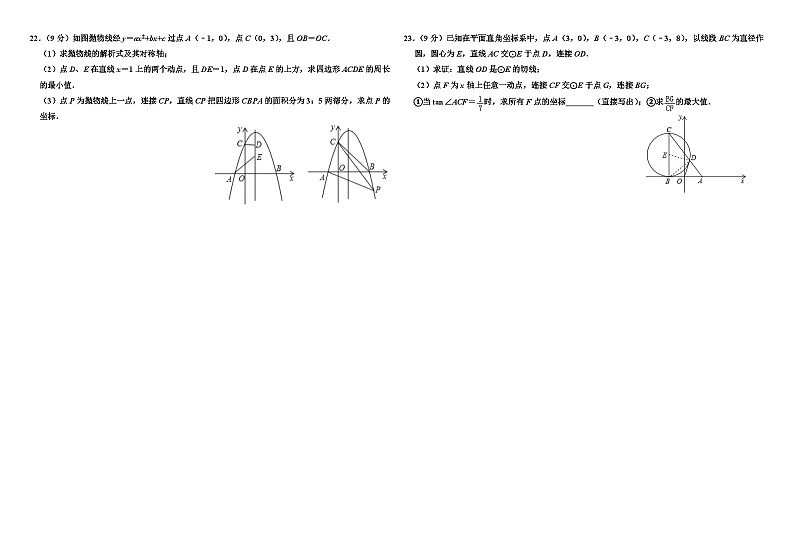
22．（9分）如图抛物线经y＝ax2+bx+c过点A（﹣1，0），点C（0，3），且OB＝OC．
（1）求抛物线的解析式及其对称轴；
（2）点D、E在直线x＝1上的两个动点，且DE＝1，点D在点E的上方，求四边形ACDE的周长的最小值．
（3）点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为3：5两部分，求点P的坐标．





















23．（9分）已知在平面直角坐标系中，点A（3，0），B（﹣3，0），C（﹣3，8），以线段BC为直径作圆，圆心为E，直线AC交⊙E于点D，连接OD．
（1）求证：直线OD是⊙E的切线；
（2）点F为x轴上任意一动点，连接CF交⊙E于点G，连接BG；
①当tan∠ACF＝时，求所有F点的坐标　 　（直接写出）；②求的最大值．


2019年广东省深圳市中考数学试卷答案
1． B．2． A．3． C．4． B．5． D．6． C．7． B．8． A．9． C．10． D．11． B．12． D．
13． a（b+1）（b﹣1）14． ．15． ．16． ．
17．解：原式＝3﹣2×+8+1
＝3﹣1+8+1
＝11．
18．解：原式＝×
＝x+2，
将x＝﹣1代入得：
原式＝x+2＝1．
19．解：（1）80÷40%＝200，x＝×100%＝15%，
故答案为：200；15%；
（2）喜欢二胡的学生数为200﹣80﹣30﹣20﹣10＝60，
补全统计图如图所示，（3）扇形统计图中“扬琴”所对扇形的圆心角是：360°×＝36°，
故答案为：36；
（4）3000×＝900，
答：该校喜爱“二胡”的学生约有有900名．
故答案为：900．

20．解：在Rt△ABD中，AB＝AD＝600，
作EM⊥AC于M，
则AM﹣DE＝500，
∴BM＝100，
在Rt△CEM中，tan53°＝＝＝，
∴CM＝800，
∴BC﹣CM＝800﹣100＝700（米），
答：隧道BC长为700米．
21．解：（1）设焚烧1吨垃圾，A发电厂发电x度，B发电厂发电y度，根据题意得：
，解得，
答：焚烧1吨垃圾，A发电厂发电300度，B发电厂发电260度；
（2）设A发电厂焚烧x吨垃圾，则B发电厂焚烧（90﹣x）吨垃圾，总发电量为y度，则
y＝300x+260（90﹣x）＝40x+23400，
∵x≤2（90﹣x），
∴x≤60，
∵y随x的增大而增大，
∴当x＝60时，y有最大值为：40×60+23400＝25800（元）．
答：A厂和B厂总发电量的最大是25800度．
22．解：（1）∵OB＝OC，∴点B（3，0），
则抛物线的表达式为：y＝a（x+1）（x﹣3）＝a（x2﹣2x﹣3）＝ax2﹣2ax﹣3a，
故﹣3a＝3，解得：a＝﹣1，
故抛物线的表达式为：y＝﹣x2+2x+3…①；
（2）ACDE的周长＝AC+DE+CD+AE，其中AC＝、DE＝1是常数，
故CD+AE最小时，周长最小，
取点C关于函数对称点C（2，3），则CD＝C′D，
取点A′（﹣1，1），则A′D＝AE，
故：CD+AE＝A′D+DC′，则当A′、D、C′三点共线时，CD+AE＝A′D+DC′最小，周长也最小，

四边形ACDE的周长的最小值＝AC+DE+CD+AE＝+A′D+DC′＝+A′C′＝+；
（3）如图，设直线CP交x轴于点E，

直线CP把四边形CBPA的面积分为3：5两部分，
又∵S△PCB：S△PCA＝EB×（yC﹣yP）：AE×（yC﹣yP）＝BE：AE，
则BE：AE，＝3：5或5：3，
则AE＝或，
即：点E的坐标为（，0）或（，0），
将点E、C的坐标代入一次函数表达式：y＝kx+3，
解得：k＝﹣6或﹣2，
故直线CP的表达式为：y＝﹣2x+3或y＝﹣6x+3…②
联立①②并解得：x＝4或8（不合题意值已舍去），
故点P的坐标为（4，﹣5）或（8，﹣45）．
23．解：（1）证明：如图1，连接DE，∵BC为圆的直径，
∴∠BDC＝90°，
∴∠BDA＝90°
∵OA＝OB
∴OD＝OB＝OA
∴∠OBD＝∠ODB
∵EB＝ED
∴∠EBD＝∠EDB
∴EBD+∠OBD＝∠EDB+∠ODB
即：∠EBO＝∠EDO
∵CB⊥x轴
∴∠EBO＝90°
∴∠EDO＝90°
∵点D在⊙E上
∴直线OD为⊙E的切线．
（2）①如图2，当F位于AB上时，过F作F1N⊥AC于N，
∵F1N⊥AC
∴∠ANF1＝∠ABC＝90°
∴△ANF∽△ABC
∴
∵AB＝6，BC＝8，
∴AC＝＝＝10，即AB：BC：AC＝6：8：10＝3：4：5
∴设AN＝3k，则NF1＝4k，AF1＝5k
∴CN＝CA﹣AN＝10﹣3k
∴tan∠ACF＝＝＝，解得：k＝
∴

即F1（，0）
如图3，当F位于BA的延长线上时，过F2作F2M⊥CA于M，
∵△AMF2∽△ABC
∴设AM＝3k，则MF2＝4k，AF2＝5k
∴CM＝CA+AM＝10+3k
∴tan∠ACF＝
解得：
∴AF2＝5k＝2
OF2＝3+2＝5
即F2（5，0）
故答案为：F1（，0），F2（5，0）．
②如图4，∵CB为直径
∴∠CGB＝∠CBF＝90°
∴△CBG∽△CFB
∴
∴BC2＝CG•CF
CF＝
∵CG2+BG2＝BC2，
∴BG2＝BC2﹣CG2
∴＝＝
∴＝
令y＝CG2（64﹣CG2）＝﹣CG4+64CG2＝﹣[（CG2﹣32）2﹣322]＝﹣（CG2﹣32）2+322
∴当CG2＝32时，
此时CG＝4
＝＝．










































2014年广东省深圳市中考数学试卷
一、 选择题（共12个小题，每小题3分，共36分.）
1．9的相反数（ ）
A.-9 B.9 C. ±9 D.
2．下列图形中是轴对称图形但不是中心对称图形的是( )
　 A． B． C． D．
3．支付宝与“快的打车”联合推出优惠，“快的打车”一夜之间红遍大江南北，据统计，2014年“快的打车”账户流水总金额达到47.3亿元，47.3亿用科学计数法表示为（ ）
A．4.73×108 B． 4.73×109 C．4.73×1010 D．4.73×1011
4．由几个大小相同的正方形组成的几何图形如图所示，则它的俯视图（ ）

A B C D
5．在-2,1,2,1,4,6中正确的是( )
A．平均数3 B.众数是-2 C.中位数是1 D.极差为8
6．已知函数y=ax+b经过（1,3）（0，-2）求a-b（ ）
A.-1 B.-3 C.3 D.7
7．下列方程没有实数根的是（ ）
A、x²+4x=10 B、3x²+8x-3=0 C、x²-2x+3=0 D、（x-2）（x-3）=12
8．如图、△ABC和△DEF中，AB=DE、角∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF（ ）
A、AC∥DF B、∠A=∠D C、AC=DF D、∠ACB=∠F
9．袋子里有4个球，标有2，3,4,5，先抽取一个并记住，放回，然后再抽取一个，文抽取的两个球数字之和大于6的概率是（ ）
A. B. C. D.
10．小明去爬山，在山脚看山顶角度为30°，小明在坡比为5:12,的山坡上走1300米，此时小明看山顶的角度为60°，求山高（ ）
A． B. C. D．
11．二次函数图像如图所示，下列正确的个数为（ ）
① ② ③ ④ 有两个解，⑤ ⑥ 当时，随增大而减小
A. 2 B. 3 C. 4 D. 5
12．如图，已知四边形ABCD为等腰梯形，AD//BC，AB=CD，E为CD中点，连接AE，且AE=，,∠DAE=30°，作AE⊥AF交BC于F，则BF=（ ）
A．1 B. C. D.







第11题 第12题 第15题
二、 填空题（每题3分，满分12分）
13．因式分解：
14．
15．如图所示，双曲线经过Rt△BOC斜边上的点A,且满足，与BC交于点D, ，求k=
16．如图，下列图形是将正三角形按一定规律排列，则第5个图形中所有正三角形的个数有





……
三、 解答题（共7小题，共72分.）
17．计算：－2tan60°＋（-1）0－()-1



18．先化简，再求值：，在-2，0，1，2四个数中选一个合适的代入求值．


项目
频数
频率
A
80
b
B
c
0.3

C
20
0.1
合计
a
1
19．关于体育选考项目统计图
（1）求出表中a，b，c的值，并将条形统计图补充完整．
表中a=　200　，b=　0.4　，c=　60　．
（2）如果有3万人参加体育选考，会有多少人选择篮球？








20．已知BD垂直平分AC，∠BCD=∠ADF，AF⊥AC，（1）证明ABDF是平行四边形
（2）若AF=DF=5，AD=6，求AC的长









21．某“爱心义卖”活动中，购进甲、乙两种文具，甲每个进货价高于乙进货价10元，90元买乙的数量与150元买甲的数量相同。（1）求甲、乙进货价；（2）甲、乙共100件，将进价提高20%进行销售，进货价少于2080元，销售额要大于2460元，求有几种方案？






22．如图，在平面直角坐标系中，⊙M过原点O，与x轴交于，与y轴交于，点C为劣弧
的中点，连接AC并延长到D，使，连接BD．（1）求⊙M的半径；（2）证明：BD为⊙M的切线；
（3）在直线MC上找一点P，使最大．











23．如图，直线AB的解析式为y=2x+4，交x轴于点A，交y轴于点B，以A为顶点的抛物线交直线AB于点D，交y轴负半轴于点C（0，-4），（1）求抛物线解析式；（2）将抛物线顶点沿着直线AB平移，此时顶点记为E，与y轴的交点记为F，求当△BEF与△BAO相似时，E点坐标；（3）记平移后抛物线与AB另一个交点为G，则与是否存在8倍的关系，若有，写出F点坐标。
















2014年广东省深圳市中考数学试卷答案
一、1． A．2． B．3． B．4． A．5．D．6． D．7． C．8． C．9． C．10．B．11． B．12．D．
二、13． 2（x+2）（x﹣2）．14．3．15． 8．16． 485．
三、17．解：原式=2﹣2+1﹣3=﹣2．
18．解：原式=•=2x+8，
当x=1时，原式=2+8=10．
19．解：（1）a=20÷0.1=200，
c=200×0.3=60，
b=80÷200=0.4，
故答案为：200，0.4，60，
补全条形统计图如下：

（2）30000×0.4=12000（人）．
答：3万人参加体育选考，会有12000人选择篮球．
20．（1）证明：∵BD垂直平分AC，
∴AB=BC，AD=DC，
在△ADB与△CDB中，
，
∴△ADB≌△CDB（SSS）
∴∠BCD=∠BAD，
∵∠BCD=∠ADF，
∴∠BAD=∠ADF，
∴AB∥FD，
∵BD⊥AC，AF⊥AC，
∴AF∥BD，
∴四边形ABDF是平行四边形，
（2）解：∵四边形ABDF是平行四边形，AF=DF=5，
∴▱ABDF是菱形，
∴AB=BD=5，
∵AD=6，
设BE=x，则DE=5﹣x，
∴AB2﹣BE2=AD2﹣DE2，
即52﹣x2=62﹣（5﹣x）2
解得：x=，
∴=，
∴AC=2AE=．
21．解：（1）设乙进货价x元，则甲进货价为（x+10）元，由题意得
=
解得x=15，
则x+10=25，
经检验x=15是原方程的根，
答：甲进货价为25元，乙进货价15元．
（2）设进甲种文具m件，则乙种文具（100﹣m）件，由题意得

解得55＜m＜58
所以m=56，57
则100﹣m=44，43．
有两种方案：进甲种文具56件，则乙种文具44件；或进甲种文具57件，则乙种文具43件．
22．（1）解：∵由题意可得出：OA2+OB2=AB2，AO=4，BO=3，
∴AB=5，
∴圆的半径为；
（2）证明：由题意可得出：M（2，）
又∵C为劣弧AO的中点，由垂径定理且 MC=，故 C（2，﹣1）
过 D 作 DH⊥x 轴于 H，设 MC 与 x 轴交于 K，
则△ACK∽△ADH，
又∵DC=4AC，
故 DH=5KC=5，HA=5KA=10，
∴D（﹣6，﹣5）
设直线AB表达式为：y=ax+b，
，
解得：
故直线AB表达式为：y=﹣x+3，
同理可得：根据B，D两点求出BD的表达式为y=x+3，
∵KAB×KBD=﹣1，
∴BD⊥AB，BD为⊙M的切线；
（3）解：取点A关于直线MC的对称点O，连接DO并延长交直线MC于P，
此P点为所求，且线段DO的长为|DP﹣AP|的最大值；
设直线DO表达式为 y=kx，
∴﹣5=﹣6k，
解得：k=，
∴直线DO表达式为 y=x
又∵在直线DO上的点P的横坐标为2，y=，
∴P（2，），
此时|DP﹣AP|=DO==．

23．解：（1）直线AB的解析式为y=2x+4，
令x=0，得y=4；令y=0，得x=﹣2．
∴A（﹣2，0）、B（0，4）．
∵抛物线的顶点为点A（﹣2，0），
∴设抛物线的解析式为：y=a（x+2）2，
点C（0，﹣4）在抛物线上，代入上式得：﹣4=4a，解得a=﹣1，
∴抛物线的解析式为y=﹣（x+2）2．
（2）平移过程中，设点E的坐标为（m，2m+4），
则平移后抛物线的解析式为：y=﹣（x﹣m）2+2m+4，
∴F（0，﹣m2+2m+4）．
①∵点E为顶点，∴∠BEF≥90°，
∴若△BEF与△BAO相似，只能是点E作为直角顶点，
∴△BAO∽△BFE，
∴，即，可得：BE=2EF．
如答图2﹣1，过点E作EH⊥y轴于点H，则点H坐标为：H（0，2m+4）．

∵B（0，4），H（0，2m+4），F（0，﹣m2+2m+4），
∴BH=|2m|，FH=|﹣m2|．
在Rt△BEF中，由射影定理得：BE2=BH•BF，EF2=FH•BF，
又∵BE=2EF，∴BH=4FH，
即：4|﹣m2|=|2m|．
若﹣4m2=2m，解得m=﹣或m=0（与点B重合，舍去）；
若﹣4m2=﹣2m，解得m=或m=0（与点B重合，舍去），此时点E位于第一象限，∠BEF为钝角，故此情形不成立．
∴m=﹣，
∴E（﹣，3）．
②假设存在．
联立抛物线：y=﹣（x+2）2与直线AB：y=2x+4，可求得：D（﹣4，﹣4），
∴S△ACD=×4×4=8．
∵S△EFG与S△ACD存在8倍的关系，
∴S△EFG=64或S△EFG=1．
联立平移抛物线：y=﹣（x﹣m）2+2m+4与直线AB：y=2x+4，可求得：G（m﹣2，2m）．
∴点E与点M横坐标相差2，即：|xG|﹣|xE|=2．

如答图2﹣2，S△EFG=S△BFG﹣S△BEF=BF•|xG|﹣BF|xE|=BF•（|xG|﹣|xE|）=BF．
∵B（0，4），F（0，﹣m2+2m+4），∴BF=|﹣m2+2m|．
∴|﹣m2+2m|=64或|﹣m2+2m|=1，
∴﹣m2+2m可取值为：64、﹣64、1、﹣1．
当取值为64时，一元二次方程﹣m2+2m=64无解，故﹣m2+2m≠64．
∴﹣m2+2m可取值为：﹣64、1、﹣1．
∵F（0，﹣m2+2m+4），
∴F坐标为：（0，﹣60）、（0，3）、（0，5）．
综上所述，S△EFG与S△ACD存在8倍的关系，点F坐标为（0，﹣60）、（0，3）、（0，5）．





2015年广东省深圳市中考数学试卷
一、选择题：（共12个小题，每小题3分，共36分.）
1．﹣15的相反数是（　　）
A．15 B．﹣15 C． D．
2．用科学记数法表示316000000为（　　）
A．3.16×107 B．3.16×108 C．31.6×107 D．31.6×106
3．下列说法错误的是（　　）
A．a•a=a2 B．2a+a=3a C．（a3）2=a5 D．a3÷a﹣1=a4
4．下列图形既是中心对称又是轴对称图形的是（　　）
A． B． C． D．
5．下列主视图正确的是（　　）
A． B． C． D．
6．在以下数据75，80，80，85，90中，众数、中位数分别是（　　）
A．75，80 B．80，80 C．80，85 D．80，90
7．解不等式2x≥x﹣1，并把解集在数轴上表示（　　）
A． B． C． D．
8．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法正确的个数是（　　）
①a＞0；②b＞0；③c＜0；④b2﹣4ac＞0．
A．1 B．2 C．3 D．4
9．如图，AB为⊙O直径，已知∠DCB=20°，则∠DBA为（　　）
A．50° B．20° C．60° D．70°

第8题 第9题 第12题
10．某商品的标价为200元，8折销售仍赚40元，则商品进价为（　　）元．
A．140 B．120 C．160 D．100
11．如图，已知△ABC，AB＜BC，用尺规作图的方法在BC上取一点P，使得PA+PC=BC，则下列选项正确的是（　　）
A． B． C． D．
12．如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=．在以上4个结论中，正确的有（　　）
A．1 B．2 C．3 D．4
二、填空题：（每题3分，满分12分）
13．因式分解：3a2﹣3b2=　 　．
14．在数字1，2，3中任选两个组成一个两位数，则这个两位数能被3整除的概率是　 　．
15．观察下列图形，它们是按一定规律排列的，依照此规律，第5个图形有　 　个太阳．

16．如图，已知点A在反比例函数y=（x＜0）上，作Rt△ABC，点D为斜边AC的中点，连DB并延长交y轴于点E．若△BCE的面积为8，则k=　 　．
三、解答题：17．计算：|2﹣|+2sin60°+﹣．




18．解方程：．



19．11月读书节，深圳市为统计某学校初三学生读书状况，如下图：
（1）三本以上的x值为　 　，参加调查的总人数为　 　，补全统计图；
（2）三本以上的圆心角为　 　．
（3）全市有6.7万学生，三本以上有　 　人．

20．小丽为了测旗杆AB的高度，小丽眼睛距地面1.5米，小丽站在C点，测出旗杆A的仰角为30°，小丽向前走了10米到达点E，此时的仰角为60°，求旗杆的高度．





21．下表为深圳市居民每月用水收费标准，（单位：元/m3）．
（1）某用户用水10立方米，共交水费23元，求a的值；
（2）在（1）的前提下，该用户5月份交水费71元，请问该用户用水多少立方米？
用水量
单价
x≤22
a
剩余部分
a+1.1







22．如图1，水平放置一个直角三角板和一个量角器，三角板的边AB和量角器的直径DE在一条直线上，AB=BC=6cm，OD=3cm，开始的时候BD=1cm，现在三角板以2cm/s的速度向右移动．
（1）当B与O重合的时候，求三角板运动的时间；（2）如图2，当AC与半圆相切时，求AD；
（3）如图3，当AB和DE重合时，求证：CF2=CG•CE．







23．如图1，关于x的二次函数y=﹣x2+bx+c经过点A（﹣3，0），点C（0，3），点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上．（1）求抛物线的解析式；（2）DE上是否存在点P到AD的距离与到x轴的距离相等？若存在求出点P，若不存在请说明理由；（3）如图2，DE的左侧抛物线上是否存在点F，使2S△FBC=3S△EBC？若存在求出点F的坐标，若不存在请说明理由．

　



2015年广东省深圳市中考数学试卷答案
一、1． A．　2． B．　3． C．4． D．5． A．6． B．7． B．8． B．　9． D．10． B．11． D．12．C．
二、13． 3（a+b）（a﹣b）14． ．15．21．16． 16．
三、17．解：原式=2﹣+2×+2﹣1=3．　
18．解：去分母得：3x2﹣2x+10x﹣15=4（2x﹣3）（3x﹣2），
整理得：3x2﹣2x+10x﹣15=24x2﹣52x+24，即7x2﹣20x+13=0，
分解因式得：（x﹣1）（7x﹣13）=0，
解得：x1=1，x2=，
经检验x1=1与x2=都为分式方程的解．
19．解：（1）40÷10%=400（人），
x=100%﹣10%﹣25%﹣45%=20%，400×20%=80（人），
故答案为：20%，400；
如图所示；

（2）20%×360°=72°，
故答案为：72°；
（3）67000×20%=13400（人），
故答案为：13400．
20．解：如图，∵∠ADG=30°，∠AFG=60°，
∴∠DAF=30°，
∴AF=DF=10，
在Rt△FGA中，
AG=AF•sin∠AFG=10×=5，
∴AB=1.5+5．
答：旗杆AB的高度为（1.5+5）米．

　
21．解：（1）由题意可得：10a=23，
解得：a=2.3，
答：a的值为2.3；
（2）设用户水量为x立方米，
∵用水22立方米时，水费为：22×2.3=50.6＜71，
∴x＞22，
∴22×2.3+（x﹣22）×（2.3+1.1）=71，
解得：x=28，
答：该用户用水28立方米．
22．（1）解：由题意可得：BO=4cm，t==2（s）；
（2）解：如图2，连接O与切点H，则OH⊥AC，
又∵∠A=45°，
∴AO=OH=3cm，
∴AD=AO﹣DO=（3﹣3）cm；
（3）证明：如图3，连接EF，
∵OD=OF，
∴∠ODF=∠OFD，
∵DE为直径，
∴∠ODF+∠DEF=90°，
∠DEC=∠DEF+∠CEF=90°，
∴∠CEF=∠ODF=∠OFD=∠CFG，
又∵∠FCG=∠ECF，
∴△CFG∽△CEF，
∴=，∴CF2=CG•CE．

　23．解：
（1）∵二次函数y=﹣x2+bx+c经过点A（﹣3，0），点C（0，3），
∴，解得，
∴抛物线的解析式y=﹣x2﹣2x+3，
（2）存在，
当P在∠DAB的平分线上时，如图1，作PM⊥AD，

设P（﹣1，m），则PM=PD•sin∠ADE=（4﹣m），PE=m，
∵PM=PE，∴（4﹣m）=m，m=﹣1，∴P点坐标为（﹣1，﹣1）；
当P在∠DAB的外角平分线上时，如图2，作PN⊥AD，

设P（﹣1，n），则PN=PD•sin∠ADE=（4﹣n），PE=﹣n，
∵PN=PE，∴（4﹣n）=﹣n，n=﹣﹣1，∴P点坐标为（﹣1，﹣﹣1）；
综上可知存在满足条件的P点，其坐标为（﹣1，﹣1）或（﹣1，﹣﹣1）；
（3）∵抛物线的解析式y=﹣x2﹣2x+3，∴B（1，0），∴S△EBC=EB•OC=3，
∵2S△FBC=3S△EBC，∴S△FBC=，
过F作FQ⊥x轴于点H，交BC的延长线于Q，过F作FM⊥y轴于点M，如图3，

∵S△FBC=S△BQH﹣S△BFH﹣S△CFQ=HB•HQ﹣BH•HF﹣QF•FM=BH（HQ﹣HF）﹣QF•FM=BH•QF﹣QF•FM=QF•（BH﹣FM）=FQ•OB=FQ=，
∴FQ=9，
∵BC的解析式为y=﹣3x+3，
设F（x0，﹣x02﹣2x0+3），
∴﹣3x0+3+x02+2x0﹣3=9，
解得：x0=或（舍去），
∴点F的坐标是（，），
∵S△ABC=6＞，
∴点F不可能在A点下方，
综上可知F点的坐标为（，）．

2016年广东省深圳市中考数学试卷
一、单项选择题：共12小题，每小题3分，共36分
1．下列四个数中，最小的正数是（　　）
A．﹣1 B．0 C．1 D．2
2．把下列图标折成一个正方体的盒子，折好后与“中”相对的字是（　　）
A．祝 B．你 C．顺 D．利

第2题 第6题 第11题 第12题
3．下列运算正确的是（　　）
A．8a﹣a=8 B．（﹣a）4=a4C．a3•a2=a6D．（a﹣b）2=a2﹣b2
4．下列图形中，是轴对称图形的是（　　）
A． B． C． D．
5．据统计，从2005年到2015年中国累积节能1570000000吨标准煤，1570000000这个数用科学记数法表示为（　　）
A．0.157×1010 B．1.57×108 C．1.57×109 D．15.7×108
6．如图，已知a∥b，直角三角板的直角顶角在直线b上，若∠1=60°，则下列结论错误的是（　　）
A．∠2=60° B．∠3=60° C．∠4=120° D．∠5=40°
7．数学老师将全班分成7个小组开展小组合作学习，采用随机抽签确定一个小组进行展示活动，则第3个小组被抽到的概率是（　　）
A． B． C． D．
8．下列命题正确的是（　　）
A．一组对边平行，另一组对边相等的四边形是平行四边形 B．两边及其一角相等的两个三角形全等
C．16的平方根是4 D．一组数据2，0，1，6，6的中位数和众数分别是2和6
9．施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x米，则根据题意所列方程正确的是（　　）
A．﹣=2 B．﹣=2 C．﹣=2 D．﹣=2
10．给出一种运算：对于函数y=xn，规定y′=nxn﹣1．例如：若函数y=x4，则有y′=4x3．已知函数y=x3，则方程y′=12的解是（　　）
A．x1=4，x2=﹣4 B．x1=2，x2=﹣2 C．x1=x2=0 D．x1=2，x2=﹣2
11．如图，在扇形AOB中∠AOB=90°，正方形CDEF的顶点C是的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2时，则阴影部分的面积为（　　）
A．2π﹣4 B．4π﹣8 C．2π﹣8 D．4π﹣4
12．如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：
①AC=FG；②S△FAB：S四边形CEFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，
其中正确的结论的个数是（　　）
A．1 B．2 C．3 D．4
二、填空题：共4小题，每小题3分，共12分
13．分解因式：a2b+2ab2+b3=　　　　　　．
14．已知一组数据x1，x2，x3，x4的平均数是5，则数据x1+3，x2+3，x3+3，x4+3的平均数是　　　　　　．
15．如图，在▱ABCD中，AB=3，BC=5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为　　　　　　．

16．如图，四边形ABCO是平行四边形，OA=2，AB=6，点C在x轴的负半轴上，将▱ABCO绕点A逆时针旋转得到▱ADEF，AD经过点O，点F恰好落在x轴的正半轴上，若点D在反比例函数y=（x＜0）的图象上，则k的值为　　　　　　．
三、解答题：共7小题，其中17题5分，18题6分，19题7分，20题8分，共52分
17．计算：|﹣2|﹣2cos60°+（）﹣1﹣（π﹣）0．








18．解不等式组：．









19．深圳市政府计划投资1.4万亿元实施东进战略．为了解深圳市民对东进战略的关注情况．某校数学兴趣小组随机采访部分深圳市民，对采访情况制作了统计图表的一部分如下：
（1）根据上述统计图可得此次采访的人数为　　　　　　人，m=　　　　　　，n=　　　　　　；
关注情况
频数
频率
A．高度关注
M
0.1
B．一般关注
100
0.5
C．不关注
30
N
D．不知道
50
0.25
（2）根据以上信息补全条形统计图；
（3）根据上述采访结果，请估计在15000名深圳市民中，高度关注东进战略的深圳市民约有　　　　　　人．




20．某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）







21．荔枝是深圳的特色水果，小明的妈妈先购买了2千克桂味和3千克糯米糍，共花费90元；后又购买了1千克桂味和2千克糯米糍，共花费55元．（每次两种荔枝的售价都不变）（1）求桂味和糯米糍的售价分别是每千克多少元；（2）如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低．







22．如图，已知⊙O的半径为2，AB为直径，CD为弦．AB与CD交于点M，将沿CD翻折后，点A与圆心O重合，延长OA至P，使AP=OA，连接PC（1）求CD的长；（2）求证：PC是⊙O的切线；（3）点G为的中点，在PC延长线上有一动点Q，连接QG交AB于点E．交于点F（F与B、C不重合）．问GE•GF是否为定值？如果是，求出该定值；如果不是，请说明理由．







23．如图，抛物线y=ax2+2x﹣3与x轴交于A、B两点，且B（1，0）（1）求抛物线的解析式和点A的坐标；（2）如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；（3）如图2，已知直线y=x﹣分别与x轴、y轴交于C、F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE．问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．

　

2016年深圳市中考数学参考答案
一、1． C．2． C．3． B．4． B．5． C．6． D．7． A．8． D．9． A．10． B．11． A．12． D．
二、13． b（a+b）2．14． 8．15． 2．16． 4．
三、17．解：|﹣2|﹣2cos60°+（）﹣1﹣（π﹣）0
=2﹣2×+6﹣1
=6．
18．解：，
解①得x＜2，
解②得x≥﹣1，
则不等式组的解集是﹣1≤x＜2．
19．解：（1）此次采访的人数为100÷0.5=200（人），m=0.1×200=20，n=30÷200=0.15；
（2）如图所示；
（3）高度关注东进战略的深圳市民约有0.1×15000=1500（人）．

20．解：如图，作AD⊥BC，BH⊥水平线，
由题意得：∠ACH=75°，∠BCH=30°，AB∥CH，
∴∠ABC=30°，∠ACB=45°，
∵AB=32m，
∴AD=CD=AB•sin30°=16m，BD=AB•cos30°=16m，
∴BC=CD+BD=（16+16）m，
则BH=BC•sin30°=（8+8）m．

21．解：（1）设桂味的售价为每千克x元，糯米糍的售价为每千克y元；
根据题意得：，
解得：；
答：桂味的售价为每千克15元，糯米糍的售价为每千克20元；
（2）设购买桂味t千克，总费用为W元，则购买糯米糍（12﹣t）千克，
根据题意得：12﹣t≥2t，
∴t≤4，
∵W=15t+20（12﹣t）=﹣5t+240，
k=﹣5＜0，
∴W随t的增大而减小，
∴当t=4时，W的最小值=220（元），此时12﹣4=8；
答：购买桂味4千克，糯米糍8千克时，所需总费用最低．
22．（1）解：如图，连接OC，
∵沿CD翻折后，点A与圆心O重合，
∴OM=OA=×2=1，CD⊥OA，
∵OC=2，
∴CD=2CM=2=2=2；
（2）证明：∵PA=OA=2，AM=OM=1，CM=CD=，∠CMP=∠OMC=90°，
∴PC===2，
∵OC=2，PO=2+2=4，
∴PC2+OC2=（2）2+22=16=PO2，
∴∠PCO=90°，
∴PC是⊙O的切线；
（3）解：GE•GF是定值，证明如下：
如图，连接GA、AF、GB，
∵点G为的中点，
∴=，
∴∠BAG=∠AFG，
又∵∠AGE=∠FGA，
∴△AGE∽△FGA，
∴=，
∴GE•GF=AG2，
∵AB为直径，AB=4，
∴∠BAG=∠ABG=45°，
∴AG=2，
∴GE•GF=8．

23．解：（1）把B（1，0）代入y=ax2+2x﹣3，
可得a+2﹣3=0，解得a=1，
∴抛物线解析式为y=x2+2x﹣3，
令y=0，可得x2+2x﹣3=0，解得x=1或x=﹣3，
∴A点坐标为（﹣3，0）；
（2）若y=x平分∠APB，则∠APO=∠BPO，
如图1，若P点在x轴上方，PA与y轴交于点B′，

由于点P在直线y=x上，可知∠POB=∠POB′=45°，
在△BPO和△B′PO中
，
∴△BPO≌△B′PO（ASA），
∴BO=B′O=1，
设直线AP解析式为y=kx+b，把A、B′两点坐标代入可得
，解得，
∴直线AP解析式为y=x+1，
联立，解得，
∴P点坐标为（，）；
若P点在x轴下方时，同理可得△BOP≌△B′OP，
∴∠BPO=∠B′PO，
又∠B′PO在∠APO的内部，
∴∠APO≠∠BPO，即此时没有满足条件的P点，
综上可知P点坐标为（，）；
（3）如图2，作QH⊥CF，交CF于点H，

∵CF为y=x﹣，
∴可求得C（，0），F（0，﹣），
∴tan∠OFC==，
∵DQ∥y轴，
∴∠QDH=∠MFD=∠OFC，
∴tan∠HDQ=，
不妨设DQ=t，DH=t，HQ=t，
∵△QDE是以DQ为腰的等腰三角形，
∴若DQ=DE，则S△DEQ=DE•HQ=×t×t=t2，
若DQ=QE，则S△DEQ=DE•HQ=×2DH•HQ=×t×t=t2，
∵t2＜t2，
∴当DQ=QE时△DEQ的面积比DQ=DE时大．
设Q点坐标为（x，x2+2x﹣3），则D（x， x﹣），
∵Q点在直线CF的下方，
∴DQ=t=x﹣﹣（x2+2x﹣3）=﹣x2﹣x+，
当x=﹣时，tmax=3，∴（S△DEQ）max=t2=，
即以QD为腰的等腰三角形的面积最大值为．
2017年广东省深圳市中考数学试卷
一、选择题：共12个小题，每小题3分，共36分.
1．﹣2的绝对值是（　　）
A．﹣2 B．2 C．﹣ D．
2．图中立体图形的主视图是（　　）
A． B． C． D．
3．随着“一带一路”建设的不断发展，我国已与多个国家建立了经贸合作关系，去年中哈铁路（中国至哈萨克斯坦）运输量达8200000吨，将8200000用科学记数法表示为（　　）
A．8.2×105 B．82×105 C．8.2×106 D．82×107
4．观察下列图形，其中既是轴对称又是中心对称图形的是（　　）
A． B． C． D．
5．如图，下列选项中，哪个不可以得到l1∥l2（　　）
A．∠1=∠2 B．∠2=∠3 C．∠3=∠5 D．∠3+∠4=180°
6．不等式组的解集为（　　）
A．x＞﹣1 B．x＜3 C．x＜﹣1或x＞3 D．﹣1＜x＜3
7．一球鞋厂，现打折促销卖出330双球鞋，比上个月多卖10%，设上个月卖出x双，列出方程（　　）
A．10%x=330 B．（1﹣10%）x=330 C．（1﹣10%）2x=330 D．（1+10%）x=330
8．如图，已知线段AB，分别以A、B为圆心，大于AB为半径作弧，连接弧的交点得到直线l，在直线l上取一点C，使得∠CAB=25°，延长AC至M，求∠BCM的度数为（　　）
A．40° B．50° C．60° D．70°
9．下列哪一个是假命题（　　）
A．五边形外角和为360° B．切线垂直于经过切点的半径
C．（3，﹣2）关于y轴的对称点为（﹣3，2） D．抛物线y=x2﹣4x+2017对称轴为直线x=2
10．某共享单车前a公里1元，超过a公里的，每公里2元，若要使使用该共享单车50%的人只花1元钱，a应该要取什么数（　　）
A．平均数 B．中位数 C．众数 D．方差
11．如图，学校环保社成员想测量斜坡CD旁一棵树AB的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知斜坡CD的长度为20m，DE的长为10cm，则树AB的高度是（　　）m．
A．20 B．30 C．30 D．40
12．如图，正方形ABCD的边长是3，BP=CQ，连接AQ，DP交于点O，并分别与边CD，BC交于点F，E，连接AE，下列结论：①AQ⊥DP；②OA2=OE•OP；③S△AOD=S四边形OECF；④当BP=1时，tan∠OAE=，其中正确结论的个数是（　　）
A．1 B．2 C．3 D．4　

第8题 第11题 第12题 第16题
二、填空题（每题3分，满分12分）
13．因式分解：a3﹣4a=　 　．
14．在一个不透明的袋子里，有2个黑球和1个白球，除了颜色外全部相同，任意摸两个球，摸到1黑1白的概率是　 　．
15．阅读理解：引入新数i，新数i满足分配律，结合律，交换律，已知i2=﹣1，那么（1+i）•（1﹣i）=　 　．
16．如图，在Rt△ABC中，∠ABC=90°，AB=3，BC=4，Rt△MPN，∠MPN=90°，点P在AC上，PM交AB于点E，PN交BC于点F，当PE=2PF时，AP=　 　．　
三、解答题17．计算：|﹣2|﹣2cos45°+（﹣1）﹣2+．



18．先化简，再求值：（ +）÷，其中x=﹣1．



类型
频数
频率
A
30
x
B
18
0.15
C
m
0.40
D
n
y
19．深圳市某学校抽样调查，A类学生骑共享单车，B类学生坐公交车、私家车等，C类学生步行，D类学生（其它），根据调查结果绘制了不完整的统计图．
（1）学生共　 　人，x=　 　，y=　 　；
（2）补全条形统计图；
（3）若该校共有2000人，骑共享单车的有　 　人．



20．一个矩形周长为56厘米．（1）当矩形面积为180平方厘米时，长宽分别为多少？
（2）能围成面积为200平方米的矩形吗？请说明理由．







21．如图，一次函数y=kx+b与反比例函数y=（x＞0）交于A（2，4），B（a，1），与x轴，y轴分别交于点C，D．21（1）直接写出一次函数y=kx+b的表达式和反比例函数y=（x＞0）的表达式；
（2）求证：AD=BC．

22．如图，线段AB是⊙O的直径，弦CD⊥AB于点H，点M是上任意一点，AH=2，CH=4．
（1）求⊙O的半径r的长度；（2）求sin∠CMD；
（3）直线BM交直线CD于点E，直线MH交⊙O于点N，连接BN交CE于点F，求HE•HF的值．






23．如图，抛物线y=ax2+bx+2经过点A（﹣1，0），B（4，0），交y轴于点C；（1）求抛物线的解析式（用一般式表示）；（2）点D为y轴右侧抛物线上一点，是否存在点D使S△ABC=S△ABD？若存在请直接给出点D坐标；若不存在请说明理由；（3）将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长．

　








2017年广东省深圳市中考数学试卷参考答案
一、1． B．2． A．3． C．4． D．5． C．6． D．7． D．8． B．9． C．10． B．11． B．12． C．
二、13．a（a+2）（a﹣2）．14． ．15． 216． 3．
三、17．解：|﹣2|﹣2cos45°+（﹣1）﹣2+，
=2﹣﹣2×+1+2，=2﹣﹣+1+2，=3．　
18．解：当x=﹣1时，
原式=×=3x+2=﹣1　
19．解：（1）由题意总人数==120人，
x==0.25，m=120×0.4=48，
y=1﹣0.25﹣0.4﹣0.15=0.2，
n=120×0.2=24，
（2）条形图如图所示，

（3）2000×0.25=500人，
故答案为500．
20．解：（1）设矩形的长为x厘米，则另一边长为（28﹣x）厘米，依题意有
x（28﹣x）=180，
解得x1=10（舍去），x2=18，
28﹣x=28﹣18=10．
故长为18厘米，宽为10厘米；
（2）设矩形的长为x厘米，则宽为（28﹣x）厘米，依题意有
x（28﹣x）=200，即x2﹣28x+200=0，
则△=282﹣4×200=784﹣800＜0，原方程无解，
故不能围成一个面积为200平方厘米的矩形．
21．解：（1）将点A（2，4）代入y=中，得，m=2×4=8，
∴反比例函数的解析式为y=，
将点B（a，1）代入y=中，得，a=8，
∴B（8，1），
将点A（2，4），B（8，1）代入y=kx+b中，得，，
∴，∴一次函数解析式为y=﹣x+5；
（2）∵直线AB的解析式为y=﹣x+5，
∴C（10，0），D（0，5），
如图，过点A作AE⊥y轴于E，过点B作BF⊥x轴于F，
∴E（0，4），F（8，0），
∴AE=2，DE=1，BF=1，CF=2，
在Rt△ADE中，根据勾股定理得，AD==，
在Rt△BCF中，根据勾股定理得，BC==，∴AD=BC．

22．解：（1）如图1中，连接OC．
∵AB⊥CD，∴∠CHO=90°，
在Rt△COH中，∵OC=r，OH=r﹣2，CH=4，
∴r2=42+（r﹣2）2，∴r=5．
（2）如图1中，连接OD．
∵AB⊥CD，AB是直径，
∴==，
∴∠AOC=∠COD，
∵∠CMD=∠COD，∴∠CMD=∠COA，∴sin∠CMD=sin∠COA==．
（3）如图2中，连接AM．
∵AB是直径，∴∠AMB=90°，∴∠MAB+∠ABM=90°，
∵∠E+∠ABM=90°，∴∠E=∠MAB，∴∠MAB=∠MNB=∠E，
∵∠EHM=∠NHFM∴△EHM∽△NHF，∴=，∴HE•HF=HM•HN，
∵HM•HN=AH•HB，∴HE•HF=AH•HB=2•（10﹣2）=16．


　
23．解：（1）∵抛物线y=ax2+bx+2经过点A（﹣1，0），B（4，0），
∴，解得，
∴抛物线解析式为y=﹣x2+x+2；
（2）由题意可知C（0，2），A（﹣1，0），B（4，0），
∴AB=5，OC=2，
∴S△ABC=AB•OC=×5×2=5，
∵S△ABC=S△ABD，
∴S△ABD=×5=，
设D（x，y），
∴AB•|y|=×5|y|=，解得|y|=3，
当y=3时，由﹣x2+x+2=3，解得x=1或x=2，此时D点坐标为（1，3）或（2，3）；
当y=﹣3时，由﹣x2+x+2=﹣3，解得x=﹣2（舍去）或x=5，此时D点坐标为（5，﹣3）；
综上可知存在满足条件的点D，其坐标为（1，3）或（2，3）或（5，﹣3）；
（3）∵AO=1，OC=2，OB=4，AB=5，
∴AC==，BC==2，
∴AC2+BC2=AB2，
∴△ABC为直角三角形，即BC⊥AC，
如图，设直线AC与直线BE交于点F，过F作FM⊥x轴于点M，

由题意可知∠FBC=45°，
∴∠CFB=45°，
∴CF=BC=2，
∴=，即=，解得OM=2， =，即=，解得FM=6，
∴F（2，6），且B（4，0），
设直线BE解析式为y=kx+m，则可得，解得，
∴直线BE解析式为y=﹣3x+12，
联立直线BE和抛物线解析式可得，解得或，
∴E（5，﹣3），∴BE==．


2018年广东省深圳市中考数学试卷
一、选择题：（共12个小题，每小题3分，共36分.）
1．6的相反数是（　　）
A．﹣6 B． C． D．6
2．260000000用科学记数法表示为（　　）
A．0.26×109 B．2.6×108 C．2.6×109 D．26×107
3．图中立体图形的主视图是（　　）
A． B． C． D．
4．观察下列图形，是中心对称图形的是（　　）
A． B． C． D．
5．下列数据：75，80，85，85，85，则这组数据的众数和极差是（　　）
A．85，10 B．85，5 C．80，85 D．80，10
6．下列运算正确的是（　　）
A．a2•a3=a6 B．3a﹣a=2a C．a8÷a4=a2 D．
7．把函数y=x向上平移3个单位，下列在该平移后的直线上的点是（　　）
A．（2，2） B．（2，3） C．（2，4） D．（2，5）
8．如图，直线a，b被c，d所截，且a∥b，则下列结论中正确的是（　　）
A．∠1=∠2 B．∠3=∠4 C．∠2+∠4=180° D．∠1+∠4=180°

9．某旅店一共70个房间，大房间每间住8个人，小房间每间住6个人，一共480个学生刚好住满，设大房间有x个，小房间有y个．下列方程正确的是（　　）
A． B． C． D．
10．如图，一把直尺，60°的直角三角板和光盘如图摆放，A为60°角与直尺交点，AB=3，则光盘的直径是（　　）
A．3 B． C．6 D．
11．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论正确是（　　）
A．abc＞0 B．2a+b＜0 C．3a+c＜0 D．ax2+bx+c﹣3=0有两个不相等的实数根
12．如图，A、B是函数y=上两点，P为一动点，作PB∥y轴，PA∥x轴，下列说法正确的是（　　）
①△AOP≌△BOP；②S△AOP=S△BOP；③若OA=OB，则OP平分∠AOB；④若S△BOP=4，则S△ABP=16
A．①③ B．②③ C．②④ D．③④
二、填空题（每题3分，满分12分）
13．分解因式：a2﹣9=　 　．
14．一个正六面体的骰子投掷一次得到正面向上的数字为奇数的概率：　 　．
15．如图，四边形ACDF是正方形，∠CEA和∠ABF都是直角且点E，A，B三点共线，AB=4，则阴影部分的面积是　 　．

16．在Rt△ABC中，∠C=90°，AD平分∠CAB，BE平分∠ABC，AD、BE相交于点F，且AF=4，EF=，则AC=　 　．
三、解答题（共7小题，共72分.）
17．（5分）计算：（）﹣1﹣2sin45°+|﹣|+（2018﹣π）0．





18．（6分）先化简，再求值：，其中x=2．




19．（7分）某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形统计图：

频数
频率
体育
40
0.4
科技
25
a
艺术
b
0.15
其它
20
0.2
请根据上图完成下面题目：
（1）总人数为　 　人，a=　 　，b=　 　．（2）请你补全条形统计图．
（3）若全校有600人，请你估算一下全校喜欢艺术类学生的人数有多少？

20．（8分）已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6，CE=12，∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于AD长为半径作弧，交EF于点B，AB∥CD．
（1）求证：四边形ACDB为△FEC的亲密菱形； （2）求四边形ACDB的面积．




21．（8分）某超市预测某饮料有发展前途，用1600元购进一批饮料，面市后果然供不应求，又用6000元购进这批饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元．（1）第一批饮料进货单价多少元？（2）若二次购进饮料按同一价格销售，两批全部售完后，获利不少于1200元，那么销售单价至少为多少元？



22．（9分）如图在⊙O中，BC=2，AB=AC，点D为AE上的动点，且cosB=．
（1）求AB的长度；（2）求AD•AE的值；（3）过A点作AH⊥BD，求证：BH=CD+DH．





23．（9分）已知顶点为A抛物线经过点，点．（1）求抛物线的解析式；（2）如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠OPM=∠MAF，求△POE的面积；
（3）如图2，点Q是折线A﹣B﹣C上一点，过点Q作QN∥y轴，过点E作EN∥x轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN1，若点N1落在x轴上，请直接写出Q点的坐标．

　





2018年广东省深圳市中考数学参考答案
一、1． A．2． B．3． B．4． D．5． A．6． B．7． D．8． B．9． A．10． D．11． C．12． B．
二、13．（a+3）（a﹣3）．14． ．15． 8．16． ．
三、17．解：原式=2﹣2×++1=3．
18．解：原式=
把x=2代入得：原式=
19．解：（1）总人数为40÷0.4=100人，
a=25÷100=0.25、b=100×0.15=15，
故答案为：100、0.25、15；
（2）补全条形图如下：

（3）估算全校喜欢艺术类学生的人数有600×0.15=90人．
20．（1）证明：∵由已知得：AC=CD，AB=DB，
由已知尺规作图痕迹得：BC是∠FCE的角平分线，
∴∠ACB=∠DCB，
又∵AB∥CD，∴∠ABC=∠DCB，
∴∠ACB=∠ABC，∴AC=AB，
又∵AC=CD，AB=DB，∴AC=CD=DB=BA∴四边形ACDB是菱形，
∵∠ACD与△FCE中的∠FCE重合，它的对角∠ABD顶点在EF上，
∴四边形ACDB为△FEC的亲密菱形；
（2）解：设菱形ACDB的边长为x，
∵四边形ACDB是菱形，∴AB∥CE，
∴∠FAB=∠FCE，∠FBA=∠E，∴△FAB∽△FCE
∴，
即，解得：x=4，
过A点作AH⊥CD于H点，
∵在Rt△ACH中，∠ACH=45°，
∴，∴四边形ACDB的面积为：．
21．解：（1）设第一批饮料进货单价为x元，则第二批饮料进货单价为（x+2）元，
根据题意得：3•=，
解得：x=8，经检验，x=8是分式方程的解．
答：第一批饮料进货单价为8元．
（2）设销售单价为m元，
根据题意得：200（m﹣8）+600（m﹣10）≥1200，
解得：m≥11．
答：销售单价至少为11元．
22．解：（1）作AM⊥BC，
∵AB=AC，AM⊥BC，BC=2BM，∴CM=BC=1，
∵cosB==，
在Rt△AMB中，BM=1，∴AB==；
（2）连接DC，
∵AB=AC，∴∠ACB=∠ABC，
∵四边形ABCD内接于圆O，∴∠ADC+∠ABC=180°，
∵∠ACE+∠ACB=180°，∴∠ADC=∠ACE，
∵∠CAE公共角，∴△EAC∽△CAD，∴=，∴AD•AE=AC2=10；
（3）在BD上取一点N，使得BN=CD，
在△ABN和△ACD中
，
∴△ABN≌△ACD（SAS），∴AN=AD，
∵AN=AD，AH⊥BD，∴NH=HD，
∵BN=CD，NH=HD，∴BN+NH=CD+HD=BH．

23．解：（1）把点代入，
解得：a=1，∴抛物线的解析式为：；
（2）由知A（，﹣2），
设直线AB解析式为：y=kx+b，代入点A，B的坐标，
得：，
解得：，∴直线AB的解析式为：y=﹣2x﹣1，
易求E（0，1），，，
若∠OPM=∠MAF，∴OP∥AF，∴△OPE∽△FAE，∴，
∴，
设点P（t，﹣2t﹣1），则：
解得，，
由对称性知；当时，也满足∠OPM=∠MAF，∴，都满足条件，
∵△POE的面积=，∴△POE的面积为或．
（3）若点Q在AB上运动，如图1，

设Q（a，﹣2a﹣1），则NE=﹣a、QN=﹣2a，
由翻折知QN′=QN=﹣2a、N′E=NE=﹣a，
由∠QN′E=∠N=90°易知△QRN′∽△N′SE，
∴==，即===2，∴QR=2、ES=，
由NE+ES=NS=QR可得﹣a+=2，
解得：a=﹣，∴Q（﹣，）；
若点Q在BC上运动，且Q在y轴左侧，如图2，

设NE=a，则N′E=a，易知RN′=2、SN′=1、QN′=QN=3，∴QR=、SE=﹣a，
在Rt△SEN′中，（﹣a）2+12=a2，
解得：a=，∴Q（﹣，2）；
若点Q在BC上运动，且点Q在y轴右侧，如图3，

设NE=a，则N′E=a，
易知RN′=2、SN′=1、QN′=QN=3，
∴QR=、SE=﹣a，
在Rt△SEN′中，（﹣a）2+12=a2，
解得：a=，∴Q（，2）．
综上，点Q的坐标为（﹣，）或（﹣，2）或（，2）．