2019年青海省中考数学试卷-（解析版）

2019年青海省中考数学试卷

一、填空题（本大题共12小题15空，每空2分，共30分）

1．﹣5的绝对值是　   　；的立方根是　   　．

2．分解因式：ma2﹣6ma+9m＝　   　；分式方程的解为　   　．

3．世界科技不断发展，人们制造出的晶体管长度越来越短，某公司研发出长度只有0.000000006米的晶体管，该数用科学记数法表示为　   　米．

4．某种药品原价每盒60元，由于医疗政策改革，价格经过两次下调后现在售价每盒48.6元，则平均每次下调的百分率为　   　．

5．如图，P是反比例函数y图象上的一点，过点P向x轴作垂线交于点A，连接OP．若图中阴影部分的面积是1，则此反比例函数的解析式为　   　．

6．如图，在直角坐标系中，已知点A（3，2），将△ABO绕点O逆时针方向旋转180°后得到△CDO，则点C的坐标是　   　．

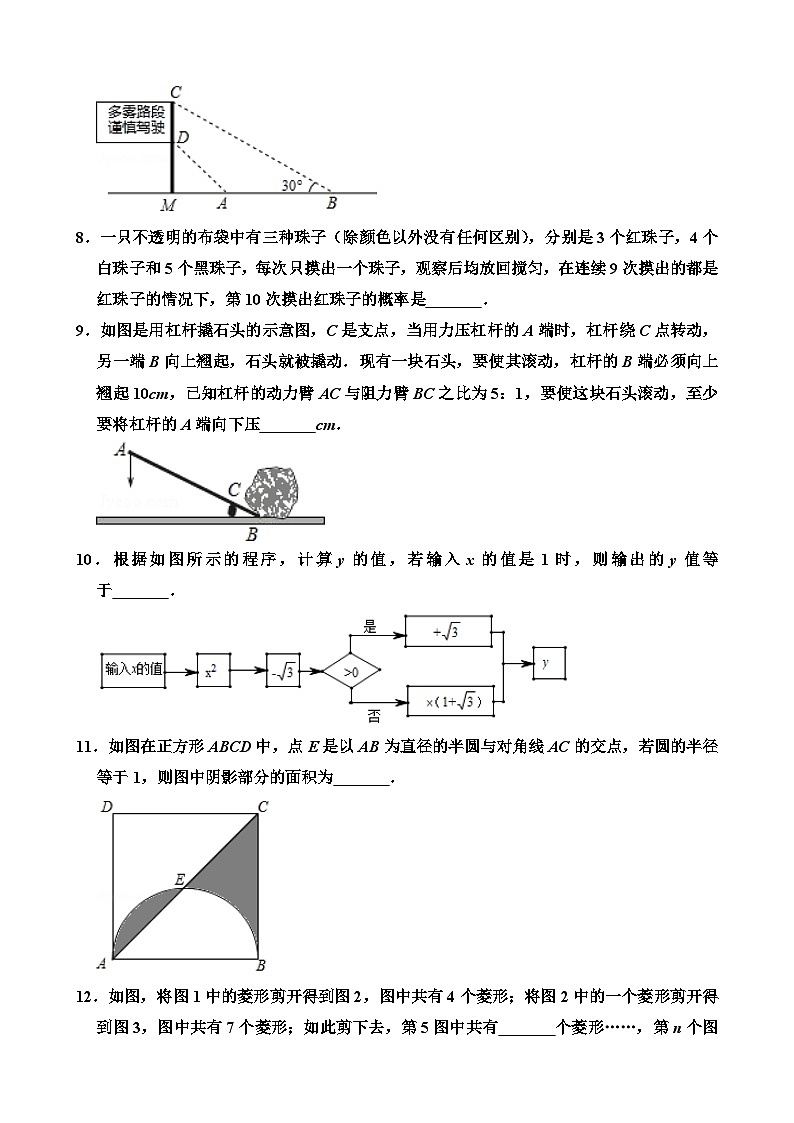
7．如图是矗立在高速公路边水平地面上的交通警示牌，经过测量得到如下数据：AM＝4米，AB＝8米，∠MAD＝45°，∠MBC＝30°，则CD的长为　   　米．（结果保留根号）

8．一只不透明的布袋中有三种珠子（除颜色以外没有任何区别），分别是3个红珠子，4个白珠子和5个黑珠子，每次只摸出一个珠子，观察后均放回搅匀，在连续9次摸出的都是红珠子的情况下，第10次摸出红珠子的概率是　   　．

9．如图是用杠杆撬石头的示意图，C是支点，当用力压杠杆的A端时，杠杆绕C点转动，另一端B向上翘起，石头就被撬动．现有一块石头，要使其滚动，杠杆的B端必须向上翘起10cm，已知杠杆的动力臂AC与阻力臂BC之比为5：1，要使这块石头滚动，至少要将杠杆的A端向下压　   　cm．

10．根据如图所示的程序，计算y的值，若输入x的值是1时，则输出的y值等于　   　．

11．如图在正方形ABCD中，点E是以AB为直径的半圆与对角线AC的交点，若圆的半径等于1，则图中阴影部分的面积为　   　．

12．如图，将图1中的菱形剪开得到图2，图中共有4个菱形；将图2中的一个菱形剪开得到图3，图中共有7个菱形；如此剪下去，第5图中共有　   　个菱形……，第n个图中共有　   　个菱形．

二、单项选择题（本大题共8小题，每小题3分，共24分）

13．下面几何体中，俯视图为三角形的是（　　）

A． B． 

C． D．

14．如图，将一副三角板和一张对边平行的纸条按下列方式摆放：两个三角板的一直角边重合，含30°角的三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（　　）

A．15° B．22.5° C．30° D．45°

15．如图所示的两台天平保持平衡，已知每块巧克力的重量相等，且每个果冻的重量也相等，则每块巧克力和每个果冻的重量分别为（　　）

A．10g，40g B．15g，35g C．20g，30g D．30g，20g

16．为了了解某班学生每周做家务劳动的时间，某综合实践活动小组对该班50名学生进行了调查，有关数据如下表，这组数据的中位数和众数为（　　）

A．2.5和2.5 B．2.25和3 C．2.5和3 D．10和13

17．如图，小莉从A点出发，沿直线前进10米后左转20°，再沿直线前进10米，又向左转20°，……，照这样走下去，她第一次回到出发点A时，一共走的路程是（　　）

A．150米 B．160米 C．180米 D．200米

18．如图，AD∥BE∥CF，直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F．已知AB＝1，BC＝3，DE＝1.2，则DF的长为（　　）

A．3.6 B．4.8 C．5 D．5，2

19．如图，在扇形AOB中，AC为弦，∠AOB＝140°，∠CAO＝60°，OA＝6，则的长为（　　）

A． B． C．2π D．2π

20．大家知道乌鸦喝水的故事，如图，它看到一个水位较低的瓶子，喝不着水，沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中，水位上升后，乌鸦喝到了水．从乌鸦看到瓶子的那刻起开始计时，设时间变量为x，水位高度变量为y，下列图象中最符合故事情景的大致图象是（　　）

A． B． 

C． D．

三、（本大题共3小题，第21题5分，第2题5分，第23题8分，共18分）

21．（5分）计算：（1）0+（）﹣1+|1|﹣2cos45°

22．（5分）化简求值：（m﹣2）；其中m1

23．（8分）如图，在△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F，连接CF．

（1）求证：△AEF≌△DEB；

（2）证明四边形ADCF是菱形．

四、（本大题共3小题，第24题9分，第25题8分，第26题9分，共26分）

24．（9分）某市为了提升菜篮子工程质量，计划用大、中型车辆共30辆调拨不超过190吨蔬菜和162吨肉制品补充当地市场．已知一辆大型车可运蔬菜8吨和肉制品5吨；一辆中型车可运蔬菜3吨和肉制品6吨．

（1）符合题意的运输方案有几种？请你帮助设计出来；

（2）若一辆大型车的运费是900元，一辆中型车的运费为600元，试说明（1）中哪种运输方案费用最低？最低费用是多少元？

25．（8分）如图，在⊙O中，点C、D分别是半径OB、弦AB的中点，过点A作AE⊥CD于点E．

（1）求证：AE是⊙O的切线；

（2）若AE＝2，sin∠ADE，求⊙O的半径．

26．（9分）“只要人人献出一点爱，世界将变成美好的人间”．某大学利用“世界献血日”开展自愿义务献血活动，经过检测，献血者血型有“A、B、AB、O”四种类型，随机抽取部分献血结果进行统计，根据结果制作了如图两幅不完整统计图表（表，图）：

血型统计表

（1）本次随机抽取献血者人数为　   　人，图中m＝　   　；

（2）补全表中的数据；

（3）若这次活动中该校有1300人义务献血，估计大约有多少人是A型血？

（4）现有4个自愿献血者，2人为O型，1人为A型，1人为B型，若在4人中随机挑选2人，利用树状图或列表法求两人血型均为O型的概率．

五、（本大题共2小题，第27题10分，第28题12分，共22分）

27．（10分）我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”，三斜即指三角形的三条边长，可以用该方法求三角形面积．若改用现代数学语言表示，其形式为：设a，b，c为三角形三边，S为面积，则S①

这是中国古代数学的瑰宝之一．

而在文明古国古希腊，也有一个数学家海伦给出了求三角形面积的另一个公式，若设p（周长的一半），则S②

（1）尝试验证．这两个公式在表面上形式很不一致，请你用以5，7，8为三边构成的三角形，分别验证它们的面积值；

（2）问题探究．经过验证，你发现公式①和②等价吗？若等价，请给出一个一般性推导过程（可以从①⇒②或者②⇒①）；

（3）问题引申．三角形的面积是数学中非常重要的一个几何度量值，很多数学家给出了不同形式的计算公式．请你证明如下这个公式：如图，△ABC的内切圆半径为r，三角形三边长为a，b，c，仍记p，S为三角形面积，则S＝pr．

28．（12分）如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点A（1，0）、B（5，0）、C（0，4）三点．

（1）求抛物线的解析式和对称轴；

（2）P是抛物线对称轴上的一点，求满足PA+PC的值为最小的点P坐标（请在图1中探索）；

（3）在第四象限的抛物线上是否存在点E，使四边形OEBF是以OB为对角线且面积为12的平行四边形？若存在，请求出点E坐标，若不存在请说明理由（请在图2中探索）

2019年青海省中考数学试卷

参考答案与试题解析

一、填空题（本大题共12小题15空，每空2分，共30分）

1．﹣5的绝对值是　5　；的立方根是　　．

【解答】解：﹣5的绝对值是5；

的立方根是．

故答案为：5，．

2．分解因式：ma2﹣6ma+9m＝　m（a﹣3）2　；分式方程的解为　x＝﹣6　．

【解答】解：原式＝m（a2﹣6a+9）＝m（a﹣3）2；

去分母得：3x＝2x﹣6，

解得：x＝﹣6，

经检验x＝﹣6是分式方程的解．

故答案为：m（a﹣3）2；x＝﹣6

3．世界科技不断发展，人们制造出的晶体管长度越来越短，某公司研发出长度只有0.000000006米的晶体管，该数用科学记数法表示为　6×10﹣9　米．

【解答】解：0.000000006＝6×10﹣9．

故答案为：6×10﹣9

4．某种药品原价每盒60元，由于医疗政策改革，价格经过两次下调后现在售价每盒48.6元，则平均每次下调的百分率为　10%　．

【解答】解：设平均每次降价的百分比是x，根据题意得：

60（1﹣x）2＝48.6，

解得：x1＝0.1＝10%，x2＝1.9（不合题意，舍去），

答：平均每次降价的百分比是10%；

故答案为：10%．

5．如图，P是反比例函数y图象上的一点，过点P向x轴作垂线交于点A，连接OP．若图中阴影部分的面积是1，则此反比例函数的解析式为　　．

【解答】解：依据比例系数k的几何意义可得，

△PAO面积等于|k|，

即|k|＝1，

k＝±，

由于函数图象位于第一、三象限，则k，

故答案为：．

6．如图，在直角坐标系中，已知点A（3，2），将△ABO绕点O逆时针方向旋转180°后得到△CDO，则点C的坐标是　（﹣3，﹣2）　．

【解答】解：由题意A，C关于原点对称，

∵A（3，2），

∴C（﹣3，﹣2），

股本答案为（﹣3，﹣2）．

7．如图是矗立在高速公路边水平地面上的交通警示牌，经过测量得到如下数据：AM＝4米，AB＝8米，∠MAD＝45°，∠MBC＝30°，则CD的长为　44　米．（结果保留根号）

【解答】解：在Rt△CMB中，∵∠CMB＝90°，MB＝AM+AB＝12米，∠MBC＝30°，

∴CM＝MB•tan30°＝124，

在Rt△ADM中，∵∠AMD＝90°，∠MAD＝45°，

∴∠MAD＝∠MDA＝45°，

∴MD＝AM＝4米，

∴CD＝CM﹣DM＝（44）米，

故答案为：44．

8．一只不透明的布袋中有三种珠子（除颜色以外没有任何区别），分别是3个红珠子，4个白珠子和5个黑珠子，每次只摸出一个珠子，观察后均放回搅匀，在连续9次摸出的都是红珠子的情况下，第10次摸出红珠子的概率是　　．

【解答】解：因为每次只摸出一个珠子时，布袋中共有珠子12个，其中红珠子3个，

所以第10次摸出红珠子的概率是．

故答案是：．

9．如图是用杠杆撬石头的示意图，C是支点，当用力压杠杆的A端时，杠杆绕C点转动，另一端B向上翘起，石头就被撬动．现有一块石头，要使其滚动，杠杆的B端必须向上翘起10cm，已知杠杆的动力臂AC与阻力臂BC之比为5：1，要使这块石头滚动，至少要将杠杆的A端向下压　50　cm．

【解答】解：如图；AM、BN都与水平线垂直，即AM∥BN；

易知：△ACM∽△BCN；

∴，

∵杠杆的动力臂AC与阻力臂BC之比为5：1，

∴，即AM＝5BN；

∴当BN≥10cm时，AM≥50cm；

故要使这块石头滚动，至少要将杠杆的端点A向下压50cm．

故答案为：50．

10．根据如图所示的程序，计算y的值，若输入x的值是1时，则输出的y值等于　﹣2　．

【解答】解：当x＝1时，x210，

∴y＝（1）（1）＝1﹣3＝﹣2，

故答案为：﹣2．

11．如图在正方形ABCD中，点E是以AB为直径的半圆与对角线AC的交点，若圆的半径等于1，则图中阴影部分的面积为　1　．

【解答】解：如图所示：连接BE，

可得，AE＝BE，∠AEB＝90°，

且阴影部分面积＝S△CEBS△ABCS正方形ABCD2×2＝1

故答案为1

12．如图，将图1中的菱形剪开得到图2，图中共有4个菱形；将图2中的一个菱形剪开得到图3，图中共有7个菱形；如此剪下去，第5图中共有　13　个菱形……，第n个图中共有　3n﹣2　个菱形．

【解答】解：（1）第1个图形有菱形1个，

第2个图形有菱形4＝1+3个，

第3个图形有菱形7＝1+3×2个，

第4个图形有菱形10＝1+3×3个，

…，

第n个图形有菱形1+3（n﹣1）＝（3n﹣2）个，

当n＝5时，3n﹣2＝13，

故答案为：13，（3n﹣2）．

二、单项选择题（本大题共8小题，每小题3分，共24分，请将正确的选项序号填入下面相应题号的表格内）

13．下面几何体中，俯视图为三角形的是（　　）

A． B． 

C． D．

【解答】解：A、俯视图为矩形；

B、俯视图为圆（带有圆心）；

C、俯视图为圆；

D、俯视图为三角形；

故选：D．

14．如图，将一副三角板和一张对边平行的纸条按下列方式摆放：两个三角板的一直角边重合，含30°角的三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（　　）

A．15° B．22.5° C．30° D．45°

【解答】解：如图，过A点作AB∥a，

∴∠1＝∠2，

∵a∥b，

∴AB∥b，

∴∠3＝∠4＝30°，

而∠2+∠3＝45°，

∴∠2＝15°，

∴∠1＝15°．

故选：A．

15．如图所示的两台天平保持平衡，已知每块巧克力的重量相等，且每个果冻的重量也相等，则每块巧克力和每个果冻的重量分别为（　　）

A．10g，40g B．15g，35g C．20g，30g D．30g，20g

【解答】解：设每块巧克力的重x克，每个果冻的重y克，由题意得：

，

解得：．

故选：C．

16．为了了解某班学生每周做家务劳动的时间，某综合实践活动小组对该班50名学生进行了调查，有关数据如下表，这组数据的中位数和众数为（　　）

A．2.5和2.5 B．2.25和3 C．2.5和3 D．10和13

【解答】解：表中数据为从小到大排列，第25个，第26个数都是2.5，故中位数是2.5；

数据3小时出现了13次最多为众数．

故选：C．

17．如图，小莉从A点出发，沿直线前进10米后左转20°，再沿直线前进10米，又向左转20°，……，照这样走下去，她第一次回到出发点A时，一共走的路程是（　　）

A．150米 B．160米 C．180米 D．200米

【解答】解：∵多边形的外角和为360°，而每一个外角为20°，

∴多边形的边数为360°÷20°＝18，

∴小莉一共走了：18×10＝180（米）．

故选：C．

18．如图，AD∥BE∥CF，直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F．已知AB＝1，BC＝3，DE＝1.2，则DF的长为（　　）

A．3.6 B．4.8 C．5 D．5，2

【解答】解：∵AD∥BE∥CF，

∴，即，

∴EF＝3.6，

∴DF＝EF+DE＝3.6+1.2＝4.8，

故选：B．

19．如图，在扇形AOB中，AC为弦，∠AOB＝140°，∠CAO＝60°，OA＝6，则的长为（　　）

A． B． C．2π D．2π

【解答】解：连接OC，

∵OA＝OC，∠CAO＝60°，

∴△AOC为等边三角形，

∴∠AOC＝60°，

∴∠BOC＝∠AOB﹣∠AOC＝140°﹣60°＝80°，

则的长，

故选：B．

20．大家知道乌鸦喝水的故事，如图，它看到一个水位较低的瓶子，喝不着水，沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中，水位上升后，乌鸦喝到了水．从乌鸦看到瓶子的那刻起开始计时，设时间变量为x，水位高度变量为y，下列图象中最符合故事情景的大致图象是（　　）

A． B． 

C． D．

【解答】解：∵乌鸦在沉思的这段时间内水位没有变化，

∴排除C，

∵乌鸦衔来一个个小石子放入瓶中，水位将会上升，

∴排除A，

∵乌鸦喝水后的水位应不低于一开始的水位，

∴排除B，

∴D正确．

故选：D．

三、（本大题共3小题，第21题5分，第2题5分，第23题8分，共18分）

21．（5分）计算：（1）0+（）﹣1+|1|﹣2cos45°

【解答】解：原式＝1﹣31﹣2

＝1﹣31

＝﹣3．

22．（5分）化简求值：（m﹣2）；其中m1

【解答】解：原式＝（）

•

，

当m1时，

原式．

23．（8分）如图，在△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F，连接CF．

（1）求证：△AEF≌△DEB；

（2）证明四边形ADCF是菱形．

【解答】证明：（1）∵AF∥BC，

∴∠AFE＝∠DBE

∵△ABC是直角三角形，AD是BC边上的中线，E是AD的中点，

∴AE＝DE，BD＝CD

在△AFE和△DBE中，

，

∴△AFE≌△DBE（AAS）

（2）由（1）知，AF＝BD，且BD＝CD，

∴AF＝CD，且AF∥BC，

∴四边形ADCF是平行四边形

∵∠BAC＝90°，D是BC的中点，

∴ADBC＝CD，

∴四边形ADCF是菱形．

四、（本大题共3小题，第24题9分，第25题8分，第26题9分，共26分）

24．（9分）某市为了提升菜篮子工程质量，计划用大、中型车辆共30辆调拨不超过190吨蔬菜和162吨肉制品补充当地市场．已知一辆大型车可运蔬菜8吨和肉制品5吨；一辆中型车可运蔬菜3吨和肉制品6吨．

（1）符合题意的运输方案有几种？请你帮助设计出来；

（2）若一辆大型车的运费是900元，一辆中型车的运费为600元，试说明（1）中哪种运输方案费用最低？最低费用是多少元？

【解答】解：（1）设安排x辆大型车，则安排（30﹣x）辆中型车，

依题意，得：，

解得：18≤x≤20．

∵x为整数，

∴x＝18，19，20．

∴符合题意的运输方案有3种，方案1：安排18辆大型车，12辆中型车；方案2：安排19辆大型车，11辆中型车；方案3：安排20辆大型车，10辆中型车．

（2）方案1所需费用为：900×18+600×12＝23400（元），

方案2所需费用为：900×19+600×11＝23700（元），

方案3所需费用为：900×20+600×10＝24000（元）．

∵23400＜23700＜24000，

∴方案1安排18辆大型车，12辆中型车所需费用最低，最低费用是23400元．

25．（8分）如图，在⊙O中，点C、D分别是半径OB、弦AB的中点，过点A作AE⊥CD于点E．

（1）求证：AE是⊙O的切线；

（2）若AE＝2，sin∠ADE，求⊙O的半径．

【解答】（1）证明：连接OA，如图，

∵点C、D分别是半径OB、弦AB的中点，

∵DC∥OA，即EC∥OA，

∵AE⊥CD，

∴AE⊥AO，

∴AE是⊙O的切线；

（2）解：连接OD，如图，

∵AD＝CD，

∴OD⊥AB，

∴∠ODA＝90°，

在Rt△AED中，sin∠ADE，

∴AD＝3，

∵CD∥OA，

∴∠OAD＝∠ADE．

在Rt△OAD中，sin∠OAD，

设OD＝2x，则OA＝3x，

∴ADx，

即x＝3，解得x，

∴OA＝3x，

即⊙O的半径长为．

26．（9分）“只要人人献出一点爱，世界将变成美好的人间”．某大学利用“世界献血日”开展自愿义务献血活动，经过检测，献血者血型有“A、B、AB、O”四种类型，随机抽取部分献血结果进行统计，根据结果制作了如图两幅不完整统计图表（表，图）：

血型统计表

（1）本次随机抽取献血者人数为　50　人，图中m＝　20　；

（2）补全表中的数据；

（3）若这次活动中该校有1300人义务献血，估计大约有多少人是A型血？

（4）现有4个自愿献血者，2人为O型，1人为A型，1人为B型，若在4人中随机挑选2人，利用树状图或列表法求两人血型均为O型的概率．

【解答】解：（1）这次随机抽取的献血者人数为5÷10%＝50（人），

所以m100＝20；

故答案为50，20；

（2）O型献血的人数为46%×50＝23（人），

A型献血的人数为50﹣10﹣5﹣23＝12（人），

故答案为12，23；

（3）从献血者人群中任抽取一人，其血型是A型的概率，

1300312，

估计这1300人中大约有312人是A型血；

（4）画树状图如图所示，

所以P（两个O型）．

五、（本大题共2小题，第27题10分，第28题12分，共22分）

27．（10分）我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”，三斜即指三角形的三条边长，可以用该方法求三角形面积．若改用现代数学语言表示，其形式为：设a，b，c为三角形三边，S为面积，则S①

这是中国古代数学的瑰宝之一．

而在文明古国古希腊，也有一个数学家海伦给出了求三角形面积的另一个公式，若设p（周长的一半），则S②

（1）尝试验证．这两个公式在表面上形式很不一致，请你用以5，7，8为三边构成的三角形，分别验证它们的面积值；

（2）问题探究．经过验证，你发现公式①和②等价吗？若等价，请给出一个一般性推导过程（可以从①⇒②或者②⇒①）；

（3）问题引申．三角形的面积是数学中非常重要的一个几何度量值，很多数学家给出了不同形式的计算公式．请你证明如下这个公式：如图，△ABC的内切圆半径为r，三角形三边长为a，b，c，仍记p，S为三角形面积，则S＝pr．

【解答】解：（1）由①得：S10，

由②得：p10，

S10；

（2）公式①和②等价；推导过程如下：

∵p，

∴2p＝a+b+c，

①中根号内的式子可化为：

（ab）（ab）

（2ab+a2+b2﹣c2）（2ab﹣a2﹣b2+c2）

[（a+b）2﹣c2][c2﹣（a﹣b）2]

（a+b+c）（a+b﹣c）（c+a﹣b）（c﹣a+b）

2p×（2p﹣2c）（2p﹣2b）（2p﹣2a）

＝p（p﹣a）（p﹣b）（p﹣c），

∴；

（3）连接OA、OB、OC，如图所示：

S＝S△AOB+S△AOC+S△BOCrcrbra＝（）r＝pr．

28．（12分）如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点A（1，0）、B（5，0）、C（0，4）三点．

（1）求抛物线的解析式和对称轴；

（2）P是抛物线对称轴上的一点，求满足PA+PC的值为最小的点P坐标（请在图1中探索）；

（3）在第四象限的抛物线上是否存在点E，使四边形OEBF是以OB为对角线且面积为12的平行四边形？若存在，请求出点E坐标，若不存在请说明理由（请在图2中探索）

【解答】解：（1）将点A、B的坐标代入二次函数表达式得：y＝a（x﹣1）（x﹣5）＝a（x2﹣6x+5），

则5a＝4，解得：a，

抛物线的表达式为：y（x2﹣6x+5）x2x+4，

函数的对称轴为：x＝3，

顶点坐标为（3，）；

（2）连接B、C交对称轴于点P，此时PA+PC的值为最小，

将点B、C的坐标代入一次函数表达式：y＝kx+b得：，

解得：，

直线BC的表达式为：yx+4，

当x＝3时，y，

故点P（3，）；

（3）存在，理由：

四边形OEBF是以OB为对角线且面积为12的平行四边形，

则S四边形OEBF＝OB×yE＝5×yE＝12，

则yE，将该坐标代入二次函数表达式得：

y（x2﹣6x+5），

解得：x＝3±，

故点E的坐标为（3，）或（3，）．