2019年浙江省金华市中考数学试卷－（4年中考）

这是一份2019年浙江省金华市中考数学试卷－（4年中考），共32页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2019年浙江省金华市中考数学试卷－（4年中考）
一、选择题（本题有10小题，每小题3分，共30分）
1.实数4的相反数是（   ）
A.      B. -4       C.        D. 4
2.计算a6÷a3,正确的结果是（   ）
A. 2    B. 3a     C. a2     D. a3
3.若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（   ）
A. 1     B. 2      C. 3     D. 8
4.某地一周前四天每天的最高气温与最低气温如表，则这四天中温差最大的是（   ）
A. 星期一   B. 星期二   C. 星期三    D. 星期四
　　　　
5.一个布袋里装有2个红球，3个黄球和5个白球，除颜色外其它都相同，搅匀后任意摸出一个球，是白球的概率为（    ）
A.      B.      C.       D. 
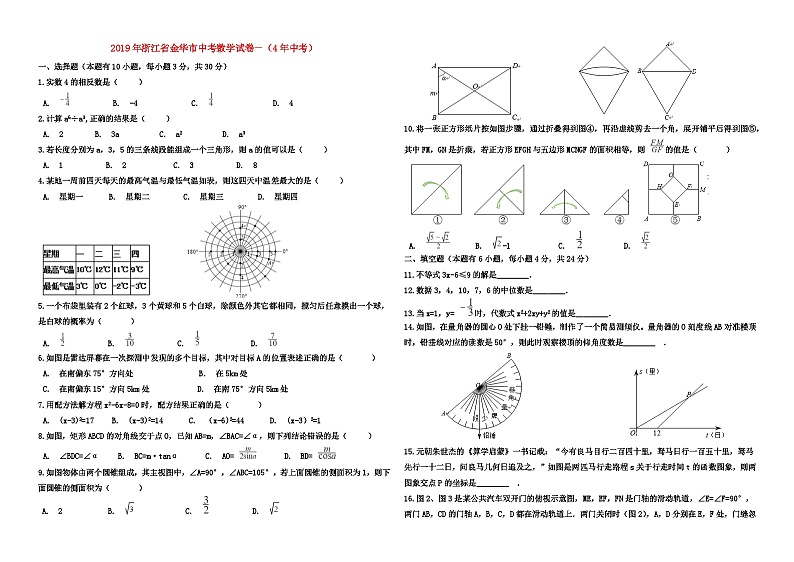
6.如图是雷达屏幕在一次探测中发现的多个目标，其中对目标A的位置表述正确的是（    ）
A. 在南偏东75°方向处  B. 在5km处   
C. 在南偏东15°方向5km处      D. 在南75°方向5km处
7.用配方法解方程x2-6x-8=0时，配方结果正确的是（    ）
A. (x-3)2=17  B. (x-3)2=14   C. （x-6)2=44   D. (x-3）2=1
8.如图，矩形ABCD的对角线交于点O，已知AB=m，∠BAC=∠α，则下列结论错误的是（   ）
A. ∠BDC=∠α  B. BC=m·tanα   C. AO=    D. BD=
9.如图物体由两个圆锥组成，其主视图中，∠A=90°，∠ABC=105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（    ）
A. 2   B.       C.      D. 
　　　　　　　
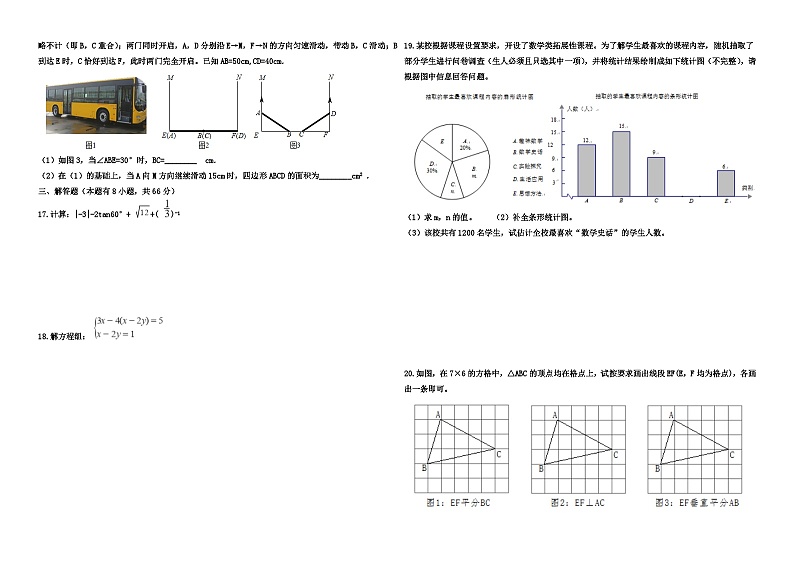
10.将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM，GN是折痕，若正方形EFGH与五边形MCNGF的面积相等，则 的值是（    ）

A.    B. -1      C.      D. 
二、填空题（本题有6小题，每小题4分，共24分）
11.不等式3x-6≤9的解是________．
12.数据3，4，10，7，6的中位数是________．
13.当x=1，y= 时，代数式x2+2xy+y2的值是________．
14.如图，在量角器的圆心O处下挂一铅锤，制作了一个简易测倾仪。量角器的O刻度线AB对准楼顶时，铅垂线对应的读数是50°，则此时观察楼顶的仰角度数是________ ．
　　　　　　　　　　　　　
15.元朝朱世杰的《算学启蒙》一书记载：“今有良马目行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之，”如图是两匹马行走路程s关于行走时间t的函数图象，则两图象交点P的坐标是________ ．
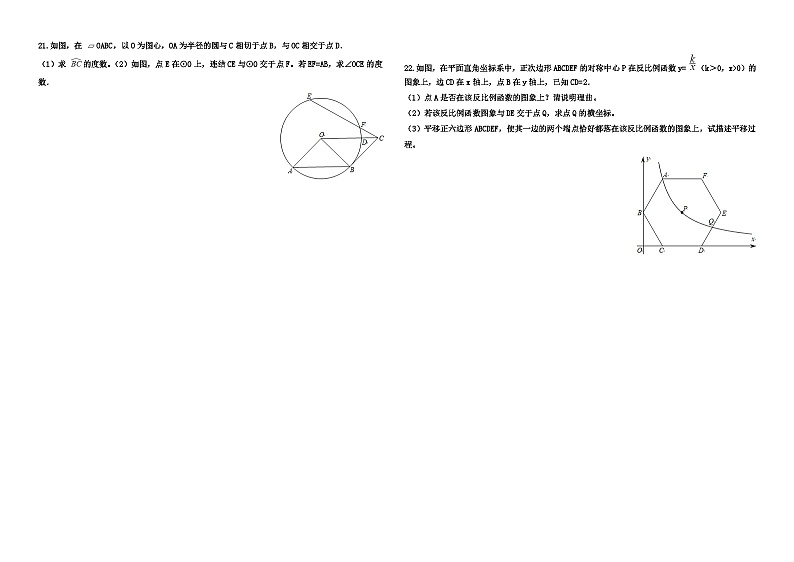
16.图2、图3是某公共汽车双开门的俯视示意图，ME，EF，FN是门轴的滑动轨道，∠E=∠F=90°，两门AB，CD的门轴A，B，C，D都在滑动轨道上．两门关闭时（图2），A，D分别在E，F处，门缝忽略不计（即B，C重合）；两门同时开启，A，D分别沿E→M，F→N的方向匀速滑动，带动B，C滑动；B到达E时，C恰好到达F，此时两门完全开启。已知AB=50cm,CD=40cm．

（1）如图3，当∠ABE=30°时，BC=________ cm．
（2）在（1）的基础上，当A向M方向继续滑动15cm时，四边形ABCD的面积为________cm2 ．
三、解答题（本题有8小题，共66分）
17.计算：|-3|-2tan60°+ +( )-1






18.解方程组：











19.某校根据课程设置要求，开设了数学类拓展性课程。为了解学生最喜欢的课程内容，随机抽取了部分学生进行问卷调查（生人必须且只选其中一项），并将统计结果绘制成如下统计图（不完整），请根据图中信息回答问题。

（1）求m，n的值。 （2）补全条形统计图。
（3）该校共有1200名学生，试估计全校最喜欢“数学史话”的学生人数。








20.如图，在7×6的方格中，△ABC的顶点均在格点上，试按要求画出线段EF(E，F均为格点)，各画出一条即可。

21.如图，在 OABC，以O为图心，OA为半径的圆与C相切于点B，与OC相交于点D．
（1）求 的度数。（2）如图，点E在⊙O上，连结CE与⊙O交于点F。若EF=AB，求∠OCE的度数．























22.如图，在平面直角坐标系中，正次边形ABCDEF的对称中心P在反比例函数y= （k＞0，x>0）的图象上，边CD在x轴上，点B在y轴上，已知CD=2．
（1）点A是否在该反比例函数的图象上？请说明理曲。
（2）若该反比例函数图象与DE交于点Q，求点Q的横坐标。
（3）平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程。



















23.如图，在平面直角坐标系中，正方形OABC的边长为4，边OA,OC分别在x轴，y轴的正半轴上,把正方形OABC的内部及边上，横，纵坐标均为整数的点称为好点，点P为抛物线y=-（x-m）2+m+2的顶点。
（1）当m=0时，求该抛物线下方（包括边界）的好点个数。
（2）当m=3时，求该抛物线上的好点坐标。
（3）若点P在正方形OABC内部，该抛物线下方（包括边界）给好存在8个好点，求m的取值范围，




















24.如图，在等腰Rt△ABC中，∠ACB=90°，AB=14 。点D，E分别在边AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF。
（1）如图1，若AD=BD，点E与点C重合，AF与DC相交于点O，求证：BD=2DO．
（2）已知点G为AF的中点。
①如图2，若AD=BD，CE=2，求DG的长。
②若AD=6BD，是否存在点E，使得△DEG是直角三角形?若存在，求CE的长；若不存在，试说明理由。
















2019年浙江省金华市中考数学试卷答案
1. B 2. D 3. C 4. C 5. A 6. D 7. A.8. C 9. D 10. A
11. x≤5 12. 6.13. .14. 40° 15. （32，4800） 16. （1）90-45 （2）2256
17. 解：原式=3-2 +2 +3, =6.
18.解：原方程可变形为： ，
①+②得：6y=6，
解得：y=1，
将y=1代入②得：
x=3，
∴原方程组的解为： .
19.（1）解：由统计表和扇形统计图可知：
A 趣味数学的人数为12人，所占百分比为20%，
∴总人数为：12÷20%=60（人），
∴m=15÷60=25%，
n=9÷60=15%，
答：m为25%，n为15%.
（2）由扇形统计图可得，
D生活应用所占百分比为：30%，
∴D生活应用的人数为：60×30%=18，
补全条形统计图如下，

（3）解：由（1）知“数学史话”的百分比为25%，
∴该校最喜欢“数学史话”的人数为：1200×25%=300（人）.
答：该校最喜欢“数学史话”的人数为300人.
20. 解：如图所示，
21.（1）如图，连结OB，设⊙O半径为r，

∵BC与⊙O相切于点B，
∴OB⊥BC，
又∵四边形OABC为平行四边形，
∴OA∥BC，AB=OC，
∴∠AOB=90°，
又∵OA=OB=r，
∴AB= r，
∴△AOB，△OBC均为等腰直角三角形，
∴∠BOC=45°，
∴弧CD度数为45°.
（2）作OH⊥EF，连结OE，
由（1）知EF=AB= r，
∴△OEF为等腰直角三角形，
∴OH= EF= r，
在Rt△OHC中，
∴sin∠OCE= = ，
∴∠OCE=30°.
22.（1）连结PC，过 点P作PH⊥x轴于点H，如图,

∵在正六边形ABCDEF中，点B在y轴上，
∴△OBC和△PCH都是含有30°角的直角三角形，BC=PC=CD=2，
∴OC=CH=1，PH= ，
∴P（2， ），
又∵点P在反比例函数y= 上，
∴k=2 ，
∴反比例函数解析式为：y= （x＞0），
连结AC，过点B作BG⊥AC于点G，
∵∠ABC=120°，AB=CB=2，
∴BG=1，AG=CG= ，AC=2 ，
∴A（1，2 ），
∴点A在该反比例函数的图像上.
（2）过点Q作QM⊥x轴于点M，
∵六边形ABCDEF为正六边形，
∴∠EDM=60°，
设DM=b，则QM= b，
∴Q（b+3， b），
又∵点Q在反比例函数上，
∴ b（b+3）=2 ,
解得：b1= ，b2= （舍去），
∴b+3= +3= ，
∴点Q的横坐标为 .
（3）连结AP，
∵AP=BC=EF，AP∥BC∥EF，
∴平移过程：将正六边形ABCDEF先向右平移1个单位，再向上平移 个单位，或将正六边形ABCDEF向左平移2个单位.
23.（1）解：∵m=0，
∴二次函数表达式为：y=-x2+2，画出函数图像如图1,
　　　
∵当x=0时，y=2；当x=1时，y=1；
∴抛物线经过点（0，2）和（1，1），
∴好点有：（0，0），（0，1），（0，2），（1，0）和（1，1），共5个.
（2）解：∵m=3，
∴二次函数表达式为：y=-（x-3）2+5，画出函数图像如图2,
∵当x=1时，y=1；当x=2时，y=4；当x=4时，y=4；
∴抛物线上存在好点，坐标分别是（1，1），（2，4）和（4，4）。
（3）解：∵抛物线顶点P（m，m+2），
∴点P在直线y=x+2上，
∵点P在正方形内部，
∴0＜m＜2，
如图3,E（2，1），F（2，2），

∴当顶点P在正方形OABC内，且好点恰好存在8个时，抛物线与线段EF有交点（点F除外），
当抛物线经过点E（2，1）时，
∴-（2-m）2+m+2=1，
解得：m1= ，m2= （舍去），
当抛物线经过点F（2，2）时，
∴-（2-m）2+m+2=2，
解得：m3=1，m4=4（舍去），
∴当 ≤m＜1时，顶点P在正方形OABC内，恰好存在8个好点.
24.（1）解：由旋转的性质得：
CD=CF，∠DCF=90°，
∵△ABC是等腰直角三角形，AD=BD，
∴∠ADO=90°，CD=BD=AD，
∴∠DCF=∠ADC，
在△ADO和△FCO中，
∵ ，
∴△ADO≌△FCO（AAS），
∴DO=CO，
∴BD=CD=2DO.
（2）解：①如图1，分别过点D、F作DN⊥BC于点N，FM⊥BC于点M，连结BF，

∴∠DNE=∠EMF=90°，
又∵∠NDE=∠MEF，DE=EF，
∴△DNE≌△EMF，
∴DN=EM，
又∵BD=7 ，∠ABC=45°，
∴DN=EM=7，
∴BM=BC-ME-EC=5，
∴MF=NE=NC-EC=5，
∴BF=5 ，
∵点D、G分别是AB、AF的中点，
∴DG= BF= ；
②过点D作DH⊥BC于点H，
∵AD=6BD，AB=14 ，
∴BD=2 ，
（ⅰ）当∠DEG=90°时，有如图2、3两种情况，设CE=t，

∵∠DEF=90°，∠DEG=90°，
∴点E在线段AF上，
∴BH=DH=2，BE=14-t，HE=BE-BH=12-t，
∵△DHE∽△ECA，
∴ ，
即 ，
解得：t=6±2 ，
∴CE=6+2 ，或CE=6-2 ，
（ⅱ）当DG∥BC时，如图4,过点F作FK⊥BC于点K，延长DG交AC于点N，延长AC并截取MN=NA，连结FM，

则NC=DH=2，MC=10，
设GN=t，则FM=2t，BK=14-2t，
∵△DHE∽△EKF，
∴DH=EK=2，HE=KF=14-2t，
∵MC=FK，
∴14-2t=10，
解得：t=2，
∵GN=EC=2，GN∥EC，
∴四边形GECN为平行四边形，∠ACB=90°，
∴四边形GECN为矩形，
∴∠EGN=90°，
∴当EC=2时，有∠DGE=90°，
（ⅲ）当∠EDG=90°时，如图5：

过点G、F分别作AC的垂线交射线于点N、M，过点E作EK⊥FM于点K，过点D作GN的垂线交NG的延长线于点P，则PN=HC=BC-HB=12，
设GN=t，则FM=2t，
∴PG=PN-GN=12-t，
∵△DHE∽△EKF，
∴FK=2，
∴CE=KM=2t-2，
∴HE=HC-CE=12-（2t-2）=14-2t，
∴EK=HE=14-2t，
AM=AC+CM=AC+EK=14+14-2t=28-2t，
∴MN= AM=14-t，NC=MN-CM=t，
∴PD=t-2，
∵△GPD∽△DHE，
∴ ，
即 ，
解得：t1=10- ，t2=10+ （舍去），
∴CE=2t-2=18-2 ；
综上所述：CE的长为=6+2 ，6-2 ，2或18-2 .












2018年浙江省金华市中考数学试卷-(word整理版)
一、选择题（本题有10小题，每小题3分，共30分）
1．在0，1，﹣，﹣1四个数中，最小的数是（　　）
A．0 B．1 C． D．﹣1
2．计算（﹣a）3÷a结果正确的是（　　）
A．a2 B．﹣a2 C．﹣a3 D．﹣a4
3．如图，∠B的同位角可以是（　　）
A．∠1 B．∠2 C．∠3 D．∠4

4．若分式的值为0，则x的值为（　　）
A．3 B．﹣3 C．3或﹣3 D．0
5．一个几何体的三视图如图所示，该几何体是（　　）
A．直三棱柱 B．长方体 C．圆锥 D．立方体
6．如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为60°，90°，210°．让转盘自由转动，指针停止后落在黄色区域的概率是（　　）
A． B． C． D．
7．小明为画一个零件的轴截面，以该轴截面底边所在的直线为x轴，对称轴为y轴，建立如图所示的平面直角坐标系．若坐标轴的单位长度取1mm，则图中转折点P的坐标表示正确的是（　　）
A．（5，30） B．（8，10） C．（9，10） D．（10，10）

8．如图，两根竹竿AB和AD斜靠在墙CE上，量得∠ABC=α，∠ADC=β，则竹竿AB与AD的长度之比为（　　）
A． B． C． D．
9．如图，将△ABC绕点C顺时针旋转90°得到△EDC．若点A，D，E在同一条直线上，∠ACB=20°，则∠ADC的度数是（　　）
A．55° B．60° C．65° D．70°

10．某通讯公司就上宽带网推出A，B，C三种月收费方式．这三种收费方式每月所需的费用y（元）与上网时间x（h）的函数关系如图所示，则下列判断错误的是（　　）
A．每月上网时间不足25 h时，选择A方式最省钱
B．每月上网费用为60元时，B方式可上网的时间比A方式多
C．每月上网时间为35h时，选择B方式最省钱
D．每月上网时间超过70h时，选择C方式最省钱　
二、填空题（本题有6小题，每小题4分，共24分）
11．化简（x﹣1）（x+1）的结果是　 　．
12．如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是　 　．

13．如图是我国2013～2017年国内生产总值增长速度统计图，则这5年增长速度的众数是　 　．
14．对于两个非零实数x，y，定义一种新的运算：x*y=+．若1*（﹣1）=2，则（﹣2）*2的值是　 　．
15．如图2，小靓用七巧板拼成一幅装饰图，放入长方形ABCD内，装饰图中的三角形顶点E，F分别在边AB，BC上，三角形①的边GD在边AD上，则的值是　 　．
16．如图1是小明制作的一副弓箭，点A，D分别是弓臂BAC与弓弦BC的中点，弓弦BC=60cm．沿AD方向拉弓的过程中，假设弓臂BAC始终保持圆弧形，弓弦不伸长．如图2，当弓箭从自然状态的点D拉到点D1时，有AD1=30cm，∠B1D1C1=120°．
（1）图2中，弓臂两端B1，C1的距离为　 　cm．
（2）如图3，将弓箭继续拉到点D2，使弓臂B2AC2为半圆，则D1D2的长为　 　cm．

三、解答题（本题有8小题，共66分）
17．（6分）计算：+（﹣2018）0﹣4sin45°+|﹣2|．








18．（6分）解不等式组：






19．（6分）为了解朝阳社区20～60岁居民最喜欢的支付方式，某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查（每人只能选择其中一项），并将调查数据整理后绘成如下两幅不完整的统计图．请根据图中信息解答下列问题：

（1）求参与问卷调查的总人数．
（2）补全条形统计图．
（3）该社区中20～60岁的居民约8000人，估算这些人中最喜欢微信支付方式的人数．










20．（8分）如图，在6×6的网格中，每个小正方形的边长为1，点A在格点（小正方形的顶点）上．试在各网格中画出顶点在格点上，面积为6，且符合相应条件的图形．

21．（8分）如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD．已知∠CAD=∠B．
（1）求证：AD是⊙O的切线．（2）若BC=8，tanB=，求⊙O的半径．
























22．（10分）如图，抛物线y=ax2+bx（a≠0）过点E（10，0），矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A（t，0），当t=2时，AD=4．
（1）求抛物线的函数表达式．
（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？
（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．




















23．（10分）如图，四边形ABCD的四个顶点分别在反比例函数y=与y=（x＞0，0＜m＜n）的图象上，对角线BD∥y轴，且BD⊥AC于点P．已知点B的横坐标为4．
（1）当m=4，n=20时．
①若点P的纵坐标为2，求直线AB的函数表达式．
②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．
（2）四边形ABCD能否成为正方形？若能，求此时m，n之间的数量关系；若不能，试说明理由．



















24．（12分）在Rt△ABC中，∠ACB=90°，AC=12．点D在直线CB上，以CA，CD为边作矩形ACDE，直线AB与直线CE，DE的交点分别为F，G．
（1）如图，点D在线段CB上，四边形ACDE是正方形．
①若点G为DE中点，求FG的长．
②若DG=GF，求BC的长．
（2）已知BC=9，是否存在点D，使得△DFG是等腰三角形？若存在，求该三角形的腰长；若不存在，试说明理由．

　

2018年浙江省金华市中考数学试卷答案
1． D．2． B．3． D．4． A．5． A．6． B．7． C．8． B．9． C．10． D．
11． x2﹣112． AC=BC．13． 6.9%．14．﹣115． ．16． 30，10﹣10，
17．解：原式=2+1﹣4×+2=2+1﹣2+2=3．　
18．解：解不等式+2＜x，得：x＞3，
解不等式2x+2≥3（x﹣1），得：x≤5，
∴不等式组的解集为3＜x≤5．
19．解：（1）（120+80）÷40%=500（人）．
答：参与问卷调查的总人数为500人．
（2）500×15%﹣15=60（人）．
补全条形统计图，如图所示．
（3）8000×（1﹣40%﹣10%﹣15%）=2800（人）．
答：这些人中最喜欢微信支付方式的人数约为2800人．

20．解：符合条件的图形如图所示；

21．（1）证明：连接OD，
∵OB=OD，
∴∠3=∠B，
∵∠B=∠1，
∴∠1=∠3，
在Rt△ACD中，∠1+∠2=90°，
∴∠4=180°﹣（∠2+∠3）=90°，
∴OD⊥AD，
则AD为圆O的切线；
（2）设圆O的半径为r，
在Rt△ABC中，AC=BCtanB=4，
根据勾股定理得：AB==4，
∴OA=4﹣r，
在Rt△ACD中，tan∠1=tanB=，
∴CD=ACtan∠1=2，
根据勾股定理得：AD2=AC2+CD2=16+4=20，
在Rt△ADO中，OA2=OD2+AD2，即（4﹣r）2=r2+20，
解得：r=．

22．解：（1）设抛物线解析式为y=ax（x﹣10），
∵当t=2时，AD=4，
∴点D的坐标为（2，4），
∴将点D坐标代入解析式得﹣16a=4，
解得：a=﹣，
抛物线的函数表达式为y=﹣x2+x；
（2）由抛物线的对称性得BE=OA=t，
∴AB=10﹣2t，
当x=t时，AD=﹣t2+t，
∴矩形ABCD的周长=2（AB+AD）
=2[（10﹣2t）+（﹣t2+t）]
=﹣t2+t+20
=﹣（t﹣1）2+，
∵﹣＜0，
∴当t=1时，矩形ABCD的周长有最大值，最大值为；
（3）如图，

当t=2时，点A、B、C、D的坐标分别为（2，0）、（8，0）、（8，4）、（2，4），
∴矩形ABCD对角线的交点P的坐标为（5，2），
当平移后的抛物线过点A时，点H的坐标为（4，4），此时GH不能将矩形面积平分；
当平移后的抛物线过点C时，点G的坐标为（6，0），此时GH也不能将矩形面积平分；
∴当G、H中有一点落在线段AD或BC上时，直线GH不可能将矩形的面积平分，
当点G、H分别落在线段AB、DC上时，直线GH过点P必平分矩形ABCD的面积，
∵AB∥CD，
∴线段OD平移后得到的线段GH，
∴线段OD的中点Q平移后的对应点是P，
在△OBD中，PQ是中位线，
∴PQ=OB=4，
所以抛物线向右平移的距离是4个单位．
23．解：（1）①如图1，∵m=4，
∴反比例函数为y=，
当x=4时，y=1，
∴B（4，1），
当y=2时，
∴2=，
∴x=2，
∴A（2，2），
设直线AB的解析式为y=kx+b，
∴，∴，
∴直线AB的解析式为y=﹣x+3；
②四边形ABCD是菱形，
理由如下：如图2，由①知，B（4，1），
∵BD∥y轴，
∴D（4，5），
∵点P是线段BD的中点，
∴P（4，3），
当y=3时，由y=得，x=，
由y=得，x=，
∴PA=4﹣=，PC=﹣4=，
∴PA=PC，
∵PB=PD，
∴四边形ABCD为平行四边形，
∵BD⊥AC，
∴四边形ABCD是菱形；
（2）四边形ABCD能是正方形，
理由：当四边形ABCD是正方形，
∴PA=PB=PC=PD，（设为t，t≠0），
当x=4时，y==，
∴B（4，），
∴A（4﹣t，+t），
∴（4﹣t）（+t）=m，
∴t=4﹣，
∴点D的纵坐标为+2t=+2（4﹣）=8﹣，
∴D（4，8﹣），
∴4（8﹣）=n，
∴m+n=32．


24．解：（1）①在正方形ACDE中，DG=GE=6，
中Rt△AEG中，AG==6，
∵EG∥AC，
∴△ACF∽△GEF，
∴=，
∴==，
∴FG=AG=2．
②如图1中，正方形ACDE中，AE=ED，∠AEF=∠DEF=45°，
∵EF=EF，
∴△AEF≌△DEF，
∴∠1=∠2，设∠1=∠2=x，
∵AE∥BC，
∴∠B=∠1=x，
∵GF=GD，
∴∠3=∠2=x，
在△DBF中，∠3+∠FDB+∠B=180°，
∴x+（x+90°）+x=180°，
解得x=30°，
∴∠B=30°，
∴在Rt△ABC中，BC==12．
（2）在Rt△ABC中，AB===15，
如图2中，当点D中线段BC上时，此时只有GF=GD，
∵DG∥AC，
∴△BDG∽△BCA，
设BD=3x，则DG=4x，BG=5x，
∴GF=GD=4x，则AF=15﹣9x，
∵AE∥CB，
∴△AEF∽△BCF，
∴=，
∴=，
整理得：x2﹣6x+5=0，
解得x=1或5（舍弃）
∴腰长GD为=4x=4．
如图3中，当点D中线段BC的延长线上，且直线AB，CE的交点中AE上方时，此时只有GF=DG，设AE=3x，则EG=4x，AG=5x，
∴FG=DG=12+4x，
∵AE∥BC，
∴△AEF∽△BCF，
∴=，
∴=，
解得x=2或﹣2（舍弃），
∴腰长DG=4x+12=20．
如图4中，当点D在线段BC的延长线上，且直线AB，EC的交点中BD下方时，此时只有DF=DG，过点D作DH⊥FG．
设AE=3x，则EG=4x，AG=5x，DG=4x+12，
∴FH=GH=DG•cos∠DGB=（4x+12）×=，
∴GF=2GH=，
∴AF=GF﹣AG=，
∵AC∥DG，
∴△ACF∽△GEF，
∴=，
∴=，
解得x=或﹣（舍弃），
∴腰长GD=4x+12=，
如图5中，当点D中线段CB的延长线上时，此时只有DF=DG，作DH⊥AG于H．
设AE=3x，则EG=4x，AG=5x，DG=4x﹣12，
∴FH=GH=DG•cos∠DGB=，
∴FG=2FH=，
∴AF=AG﹣FG=，
∵AC∥EG，
∴△ACF∽△GEF，
∴=，
∴=，
解得x=或﹣（舍弃），
∴腰长DG=4x﹣12=，
综上所述，等腰三角形△DFG的腰长为4或20或或．



























2016年浙江省金华市中考数学试卷-(word整理版)
一、选择题(有10小题,每小题3分,共30分)
1.实数的绝对值是（ )
b
0
a
（第2题图）
A.2 B. C. D.
2.若实数在数轴上的位置如图所示，则下列判断错误的是（ )
A． B. C． D．互为倒数
3.如图是加工零件的尺寸要求，现有下列直径尺寸的产品（单位：mm),其中不合格的是（ )
A.45.02 B.44.9 C.44.98 D.45.01
A B C D
主视方向
单位：mm
（第3题图）






4.从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体，得到的几何体如图所示，则该几何体的左视图正确的是（ )
5.一元二次方程的两根为，则下列结论正确的是（ )
A. B.
C. D.
（第9题图）
A
E
C
D
B
6.如图，已知，添加下列条件还不能判定△ABC≌△BAD的是（ )
C
B
A

4
（第8题图）
1
单位：米
A
B
（第6题图）
D
C
A. AC=BD B.∠CAB＝∠DBA C.∠C＝∠D D.BC=AD






7.小明和小华参加社会实践活动，随机选择“打扫社区卫生”和“参加社会调查”其中一项，那么两人同时选择“参加社会调查”的概率为（ )
A. B. C. D.
8.一座楼梯的示意图如图所示，BC是铅垂线，CA是水平线，BA与CA的夹角为.现要在楼梯上铺一条地毯，已知CA=4米，楼梯宽度1米，则地毯的面积至少需要（ )
A. 米2 B. 米2 C. 米2 D. 米2
9.足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好.如图的正方形网格中，点A,B,C,D,E均在格点上,球员带球沿CD方向进攻，最好的射点在（ )
A.点C B.点D或点E C.线段DE(异于端点) 上一点 D.线段CD(异于端点) 上一点
D
A
H
B
C
A B C D
x
2
4
x
2
O
4
O
y
x
O
4
2
y
y
1
4
O
x
y
（第10题图）
10.在四边形ABCD中，∠B=90°，AC=4，AB∥CD,DH垂直平分AC，点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为（ )



二、填空题 (有6小题,每小题4分,共24分)
11.不等式的解是 .
12.能够说明“不成立”的x的值是 （写出一个即可）.
13.为监测某河道水质，进行了6次水质检测，绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L，则第3次检测得到的氨氮含量是 mg/L.

6
2.5
2.0
1.5
1.0
0.5
5
4
3
2
1
1.5
1.4
1.5
2
1.6
0
次数
含量（mg/L）
水质检测中氨氮含量统计图
B
D
C
E
A
（第13题图） （第14题图） （第15题图）


B
A
D
E
C
B′









14.如图,已知AB∥CD，BC∥DE.若∠A＝20°，∠C＝120°，则∠AED的度数是 .
15.如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC 上，以AD为折痕将
△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形，则BD的长是 .
16.由6根钢管首尾顺次铰接而成六边形钢架ABCDEF，相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米，BC=CD=EF=FA=2米.
（铰接点长度忽略不计）
（1）转动钢管得到三角形钢架，如图1,则点A，E之间的距离是 米.
（2）转动钢管得到如图2所示的六边形钢架，有∠A=∠B=∠C=∠D=120°，现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 米.
（第16题图1） （第16题图2）

B
D
C
E
A
F
B
D
C
E
A
F








三、解答题 (有8小题,共66分,各小题都必须写出解答过程)
17．(6分)计算： .











18.（6分） 解方程组


















19.（6分）某校组织学生排球垫球训练，训练前后，对每个学生进行考核.现随机抽取部分学生，统计了训练前后两次考核成绩，并按“A，B，C”三个等次绘制了如图不完整的统计图.试根据统计
图信息,解答下列问题：
（1）抽取的学生中，训练后“A”等次的人数是多少？并补全统计图.
（2）若学校有600名学生，请估计该校训练后成绩为“A”等次的人数.
5
0
20
10
25
15
21
2
7
8
2
学校部分学生排球垫球训练前后
两次考核成绩等次统计图
人数
（第19题图）
B
A
C
等次
训练前

训练后






















20.（8分）如图1表示同一时刻的韩国首尔时间和北京时间，两地时差为整数.
（1）设北京时间为x（时），首尔时间为y（时）,就0≤x≤12，求关于的函数表达式，并填写下表（同一时刻的两地时间）.
北京时间
7:30

2:50
首尔时间

12:15

（2）如图2表示同一时刻的英国伦敦时间（夏时制）和北京时间，两地时差为整数.如果现在伦敦（夏时制）时间为7：30，那么此时韩国首尔时间是多少？
首尔 北京 伦敦（夏时制） 北京


（第20题图1） （第20题图2）







































21.（8分）如图，直线与x,y轴分别交于点A,B,与反比例函数（k＞0）图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
（1）求点A的坐标.
（2）若AE=AC.
（第21题图）
A
C
D
E
B
O
x
y
①求k的值.②试判断点E与点D是否关于原点O成中心对称？并说明理由.







































22.（10分）四边形ABCD的对角线交于点E，有AE=EC,BE=ED,以AB为直径的半圆过点E，圆心为O.
（1）利用图1，求证：四边形ABCD是菱形.
（2）如图2，若CD的延长线与半圆相切于点F，已知直径AB=8.
①连结OE,求△OBE的面积.②求弧AE的长.
C
B
A
D
E
O
B
A
D
E
C
O
F
（第22题图1） （第22题图2）










































23.（10分）在平面直角坐标系中，点O为原点，平行于x轴的直线与抛物线L：y=ax2相交于A,B两点（点B在第一象限），点D在AB的延长线上.
（1）已知a=1，点B的纵坐标为2.
①如图1，向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2，若BD=AB，过点B,D的抛物线L2，其顶点M在x轴上，求该抛物线的函
数表达式.
（2）如图3，若BD=AB，过O,B,D三点的抛物线L3，顶点为P,对应函数的二次项系数为a3，过点P作PE∥x轴，交抛物线L于E,F两点, 求的值，并直接写出的值.
（第23题图1） （第23题图2） （第23题图3）
P
D
A
B
O
x
y
L
L3
F
E
B
O
x
y
L
A
C
L1
B
O
x
y
L
A
D
L2
M





































24.(12分)在平面直角坐标系中，点O为原点，点A的坐标为(－6，0).如图1，正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.
（1）如图2，若α=60°,OE=OA，求直线EF的函数表达式.
（2）若α为锐角，，当AE取得最小值时，求正方形OEFG的面积.
（3）当正方形OEFG的顶点F落在y轴上时，直线AE与直线FG相交于点P，△OEP的其中两边之比能否为？若能，求点P的坐标；若不能，试说明理由.
（第24题图1） （第24题图2）

A
O
x
B
C
D
y
E
F
G
α
A
O
x
E
F
G
y
α







































2016年浙江省金华市中考数学试卷答案
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
B
C
C
A
A
D
C
D
11. 12. 如等（只要填一个负数即可） 13.1 14. 80°
15. 2或5（各2分） 16.（1） ；（2）
17．原式＝3－1－3×＋1
＝0.
18.
由 ①－②，得y＝3.
把y＝3代入②，得x＋3＝2，解得x＝－1.
∴原方程组的解是
19. （1）∵抽取的人数为21＋7＋2＝30，
∴训练后“A”等次的人数为30－2－8＝20.
部分学生排球垫球训练
前后二次考核成绩等次统计图
5
0
20
10
25
15
21
2
7
8
2
人数
（第19题图）
B
A
C
等次
训练前

训练后

20
如图：








（2）该校600名学生，训练后成绩为“A”等次的人数为600×= 400.
答：估计该校九年级训练后成绩为“A”等次的人数是400.
20（1）从图1看出，同一时刻，首尔时间比北京时间多1小时，
所以，关于的函数表达式是y＝x＋1.


北京时间
7:30
11:15
2:50
首尔时间
8:30
12:15
3:50

（2）从图2看出，设伦敦（夏时制）时间为t时，则北京时间为（t+7）时，
由第（1）题，韩国首尔时间为（t+8）时，
所以，当伦敦（夏时制）时间为7:30，韩国首尔时间为15:30.
21.（8分）
（1）当y＝0时，得0＝x－，解得x＝3.
∴点A的坐标为(3,0).

（2）①过点C作CF⊥x轴于点F.
设AE=AC=t, 点E的坐标是.
在Rt△AOB中， tan∠OAB=,∴∠OAB=30°.
在Rt△ACF中，∠CAF=30°, ∴，
∴点C的坐标是.
A
C
D
E
B
O
x
y
F
∴, 解得（舍去），.
所以，.
②点E的坐标为(3，2)，
设点D的坐标是,
∴，解得，,
∴点D的坐标是,
（第21题图）
所以，点E与点D关于原点O成中心对称.

22.（10分）
（1）∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形.
∵AB为直径，且过点E，
∴∠AEB=90°，即AC⊥BD.
而四边形ABCD是平行四边形，
∴四边形ABCD是菱形.
B
A
D
E
C
O
F
H
（2）①连结OF.
∵CD的延长线与半圆相切于点F，
∴OF⊥CF.
∵FC∥AB,
（第22题图）
∴OF即为△ABD的AB边上的高.
S△ABD.
∵点O，E分别是AB,BD的中点，
∴,
所以，S△OBE=S△ABE=4.
②过点D作DH⊥AB于点H.
∵AB∥CD，OF⊥CF,
∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°.
∴四边形OHDF为矩形,即DH=OF=4.
在Rt△DAH中，sin∠DAB＝＝, ∴∠DAH=30°.
∵点O,E分别为AB,BD中点，
∴OE∥AD,
∴∠EOB＝∠DAH=30°.
∴∠AOE＝180°－∠EOB＝150°.
∴弧AE的长=.
23.（10分）
（1）①对于二次函数y=x2，当y＝2时，2＝x2，解得x1＝，x2＝－，
B
O
x
y
L
A
D
L2
N
M
∴AB＝.
∵平移得到的抛物线L1经过点B，∴BC＝AB＝，
∴AC＝.
② 记抛物线L2的对称轴与AD相交于点N,
根据抛物线的轴对称性，得,
（第23题图1）
∴.
设抛物线L2的函数表达式为.
由①得，B点的坐标为,
P
D
A
B
O
x
y
L1
L3
F
E
G
H
K
Q
∴，解得a=4.
抛物线L2的函数表达式为.
（2）如图，抛物线L3与x轴交于点G,其对称轴与x轴交于点Q,
过点B作BK⊥x轴于点K.
设OK=t,则AB=BD=2t, 点B的坐标为(t，at2)，
根据抛物线的轴对称性，得OQ=2t,OG=2OQ=4t.
（第23题图2）
设抛物线L3的函数表达式为，
∵该抛物线过点B(t，at2)，
∴，因t≠0，得.
.
图1

A
O
x
E
F
G
y
M
H
24.(12分)
（1）如图1，过点E作EH⊥OA于点H，EF与y轴的交点为M.
∵OE＝OA，α＝60°，∴△AEO为正三角形，
∴OH＝3，EH＝＝3. ∴E(﹣3,3).
∵∠AOM＝90°，∴∠EOM＝30°.
在Rt△EOM中，
∵cos∠EOM＝ ，即＝ ，∴OM＝4.
∴M(0，4).
设直线EF的函数表达式为y＝kx＋4，
∵该直线过点E(﹣3,3), ∴,解得，
图2

A
O
x
E
F
G
y
α
Q
所以，直线EF的函数表达式为.
（2）如图2，射线OQ与OA的夹角为α( α为锐角，).
无论正方形边长为多少，绕点O旋转角α后得到正方
形OEFG的顶点E在射线OQ上，
∴当AE⊥OQ时，线段AE的长最小.
在Rt△AOE中，设AE＝a，则OE＝2a，
∴a2＋(2a)2＝62，解得a1＝，a2＝－(舍去),
∴OE＝2a＝, ∴S正方形OEFG＝OE2=.
（3）设正方形边长为m.
当点F落在y轴正半轴时.
如图3，当P与F重合时，△PEO是等腰直角三角形，有或.
在Rt△AOP中，∠APO＝45°，OP=OA=6,
图3 图4 图5
A
O
x
E
F
G
P
y
A
O
x
E
F
G
y
(P)
A
O
x
E
F
G
P
y
R
H
∴点P1的坐标为(0,6).









在图3的基础上，当减小正方形边长时，点P在边FG 上，△OEP的其中两边之比不可能为；当增加正方形边长时，存在（图4）和（图5）两种情况.
如图4，△EFP是等腰直角三角形，有＝，即＝, 此时有AP∥OF.
在Rt△AOE中，∠AOE＝45°，∴OE=OA＝6,
∴PE＝OE＝12，PA=PE+AE=18,
∴点P2的坐标为(－6,18).
如图5，过P作PR⊥x轴于点R，延长PG交x轴于点H.设PF=n.
在Rt△POG中，PO2＝PG2＋OG2＝m2＋(m＋n) 2＝2m2＋2mn＋n2，
在Rt△PEF中，PE2＝PF2＋EF2＝m 2＋n 2,
当＝时，∴PO2＝2PE2. ∴2m2＋2mn＋n2=2(m 2＋n 2), 得n＝2m.
∵EO∥PH，∴△AOE∽△AHP,∴,
A
O
x
E
F
G
(P)
y
图6
∴AH=4OA=24，即OH=18，∴.
在等腰Rt△PR H中，，
∴OR=RH-OH=18，
∴点P3的坐标为(－18,36).
当点F落在y轴负半轴时，
如图6，P与A重合时，在Rt△POG中，OP＝OG，
又∵正方形OGFE中，OG=OE, ∴OP＝OE.
∴点P4的坐标为(－6,0).
在图6的基础上，当正方形边长减小时，△OEP的其中
两边之比不可能为；当正方形边长增加时，存在（图7）这一种情况.
如图7，过P作PR⊥x轴于点R,设PG=n.
A
O
x
E
F
G
P
y


R
N

图7
在Rt△OPG中，PO2=PG2＋OG2＝n2＋m2，
在Rt△PEF中，PE2＝PF2＋FE2＝(m+n ) 2＋m2＝2m2＋2mn＋n 2.
当＝时，∴PE2＝2PO2.
∴2m2＋2mn＋n 2＝2n2＋2m2 ∴n=2m,
由于NG=OG=m,则PN=NG=m,
∵OE∥PN，∴△AOE∽△ANP, ∴,
即AN=OA=6.
在等腰Rt△ONG中，, ∴， ∴,
在等腰Rt△PRN中，，
∴点P5的坐标为(－18,6).
所以，△OEP的其中两边的比能为，点P的坐标是：P1(0,6)，P2(－6,18)，
P3(－18,36)，P4(－6,0)，P5(－18,6).









































2017年浙江省金华市中考数学试卷-(word整理版)
一、选择题（共10小题；共50分）
1. 下列各组数中，把两数相乘，积为 1 的是   
A. 2 和 -2 B. -2 和 12 C. 3 和 33 D. 3 和 -3

2. 一个几何体的三视图如图所示，这个几何体是   
A. 球 B. 圆柱 C. 圆锥 D. 立方体


3. 下列各组数中，不可能成为一个三角形三边长的是   
A. 2，3，4 B. 5，7，7 C. 5，6，12 D. 6，8，10

4. 在直角三角形 ABC 中，∠C=90∘，AB=5，BC=3，则 tanA 的值是   
A. 34 B. 43 C. 35 D. 45

5. 在下列的计算中，正确的是   
A. m3+m2=m5 B. m5÷m2=m3
C. 2m3=6m3 D. m+12=m2+1

6. 对于二次函数 y=-x-12+2 的图象与性质，下列说法正确的是   
A. 对称轴是直线 x=1，最小值是 2 B. 对称轴是直线 x=1，最大值是 2
C. 对称轴是直线 x=-1，最小值是 2 D. 对称轴是直线 x=-1，最大值是 2

7. 如图，在半径为 13 cm 的圆形铁片上切下一块高为 8 cm 的弓形铁片，则弓形弦 AB 的长为   
A. 10 cm B. 16 cm C. 24 cm D. 26 cm

8. 某校举行以“激情五月，唱响青春”为主题的演讲比赛．决赛阶段只剩下甲、乙、丙、丁四名同学，则甲、乙同学获得前两名的概率是   
A. 12 B. 13 C. 14 D. 16

9. 若关于 x 的一元一次不等式组 2x-1>3x-2,x