2019年浙江省金华市中考数学试卷及答案

这是一份2019年浙江省金华市中考数学试卷及答案，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
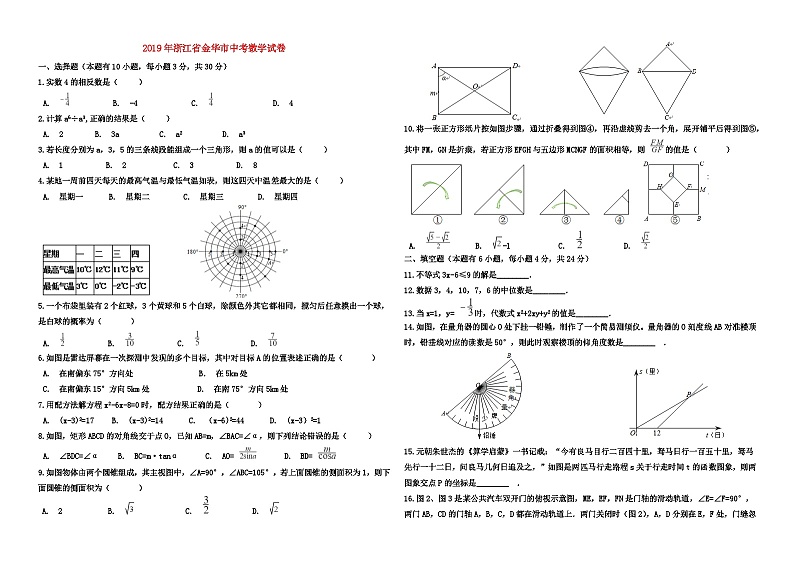
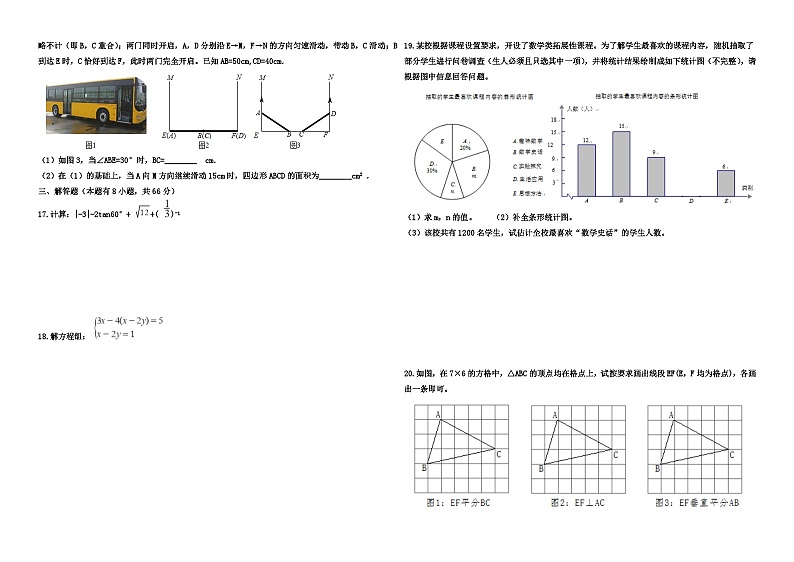
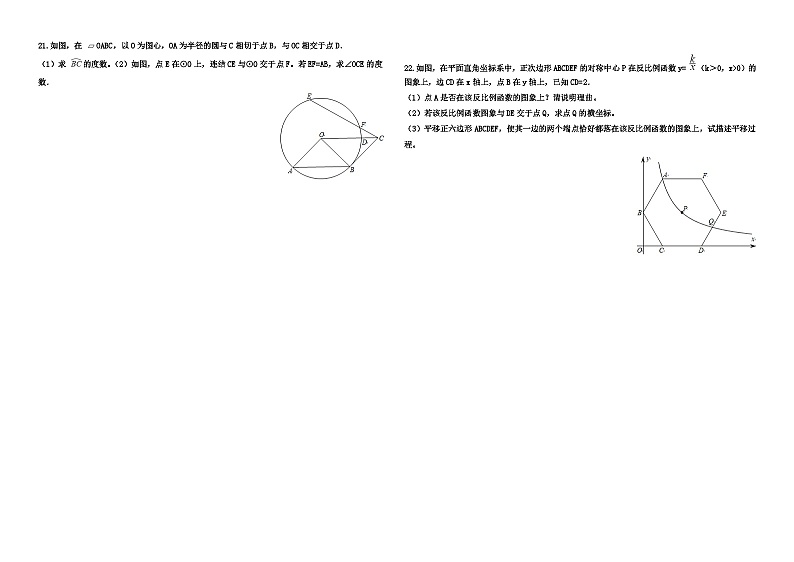
2019年浙江省金华市中考数学试卷一、选择题（本题有10小题，每小题3分，共30分）1.实数4的相反数是（   ）            A.      B. -4       C.        D. 42.计算a6÷a3,正确的结果是（   ）            A. 2    B. 3a     C. a2     D. a33.若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（   ）            A. 1     B. 2      C. 3     D. 84.某地一周前四天每天的最高气温与最低气温如表，则这四天中温差最大的是（   ）  A. 星期一   B. 星期二      C. 星期三    D. 星期四　　　　5.一个布袋里装有2个红球，3个黄球和5个白球，除颜色外其它都相同，搅匀后任意摸出一个球，是白球的概率为（    ）            A.      B.      C.       D. 6.如图是雷达屏幕在一次探测中发现的多个目标，其中对目标A的位置表述正确的是（    ）  A. 在南偏东75°方向处               B. 在5km处   C. 在南偏东15°方向5km处      D. 在南75°方向5km处7.用配方法解方程x2-6x-8=0时，配方结果正确的是（    ）            A. (x-3)2=17  B. (x-3)2=14   C. （x-6)2=44   D. (x-3）2=18.如图，矩形ABCD的对角线交于点O，已知AB=m，∠BAC=∠α，则下列结论错误的是（   ）  A. ∠BDC=∠α  B. BC=m·tanα   C. AO=    D. BD= 9.如图物体由两个圆锥组成，其主视图中，∠A=90°，∠ABC=105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（    ）   A. 2         B.       C.      D. 　　　　　　　10.将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM，GN是折痕，若正方形EFGH与五边形MCNGF的面积相等，则 的值是（    ）   A.    B. -1      C.      D. 二、填空题（本题有6小题，每小题4分，共24分）11.不等式3x-6≤9的解是________．    12.数据3，4，10，7，6的中位数是________．    13.当x=1，y= 时，代数式x2+2xy+y2的值是________．    14.如图，在量角器的圆心O处下挂一铅锤，制作了一个简易测倾仪。量角器的O刻度线AB对准楼顶时，铅垂线对应的读数是50°，则此时观察楼顶的仰角度数是________ ．   　　　　　　　　　　　　　15.元朝朱世杰的《算学启蒙》一书记载：“今有良马目行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之，”如图是两匹马行走路程s关于行走时间t的函数图象，则两图象交点P的坐标是________ ．  16.图2、图3是某公共汽车双开门的俯视示意图，ME，EF，FN是门轴的滑动轨道，∠E=∠F=90°，两门AB，CD的门轴A，B，C，D都在滑动轨道上．两门关闭时（图2），A，D分别在E，F处，门缝忽略不计（即B，C重合）；两门同时开启，A，D分别沿E→M，F→N的方向匀速滑动，带动B，C滑动；B到达E时，C恰好到达F，此时两门完全开启。已知AB=50cm,CD=40cm．   （1）如图3，当∠ABE=30°时，BC=________ cm．    （2）在（1）的基础上，当A向M方向继续滑动15cm时，四边形ABCD的面积为________cm2 ．    三、解答题（本题有8小题，共66分）17.计算：|-3|-2tan60°+ +( )-1          18.解方程组：            19.某校根据课程设置要求，开设了数学类拓展性课程。为了解学生最喜欢的课程内容，随机抽取了部分学生进行问卷调查（生人必须且只选其中一项），并将统计结果绘制成如下统计图（不完整），请根据图中信息回答问题。   （1）求m，n的值。    （2）补全条形统计图。    （3）该校共有1200名学生，试估计全校最喜欢“数学史话”的学生人数。            20.如图，在7×6的方格中，△ABC的顶点均在格点上，试按要求画出线段EF(E，F均为格点)，各画出一条即可。   21.如图，在 OABC，以O为图心，OA为半径的圆与C相切于点B，与OC相交于点D．  （1）求 的度数。（2）如图，点E在⊙O上，连结CE与⊙O交于点F。若EF=AB，求∠OCE的度数．                          22.如图，在平面直角坐标系中，正次边形ABCDEF的对称中心P在反比例函数y= （k＞0，x>0）的图象上，边CD在x轴上，点B在y轴上，已知CD=2．  （1）点A是否在该反比例函数的图象上？请说明理曲。    （2）若该反比例函数图象与DE交于点Q，求点Q的横坐标。    （3）平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程。                      23.如图，在平面直角坐标系中，正方形OABC的边长为4，边OA,OC分别在x轴，y轴的正半轴上,把正方形OABC的内部及边上，横，纵坐标均为整数的点称为好点，点P为抛物线y=-（x-m）2+m+2的顶点。  （1）当m=0时，求该抛物线下方（包括边界）的好点个数。    （2）当m=3时，求该抛物线上的好点坐标。    （3）若点P在正方形OABC内部，该抛物线下方（包括边界）给好存在8个好点，求m的取值范围，                       24.如图，在等腰Rt△ABC中，∠ACB=90°，AB=14 。点D，E分别在边AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF。  （1）如图1，若AD=BD，点E与点C重合，AF与DC相交于点O，求证：BD=2DO．    （2）已知点G为AF的中点。  ①如图2，若AD=BD，CE=2，求DG的长。②若AD=6BD，是否存在点E，使得△DEG是直角三角形?若存在，求CE的长；若不存在，试说明理由。                2019年浙江省金华市中考数学试卷答案1. B   2. D   3. C   4. C   5. A   6. D   7. A.8. C   9. D   10. A   11. x≤5   12. 6.13. .14. 40°   15. （32，4800）   16. （1）90-45 （2）2256   17. 解：原式=3-2 +2 +3,   =6.18.解：原方程可变形为： ，①+②得：6y=6，解得：y=1，将y=1代入②得：x=3，∴原方程组的解为： .19.（1）解：由统计表和扇形统计图可知：   A 趣味数学的人数为12人，所占百分比为20%，∴总人数为：12÷20%=60（人），∴m=15÷60=25%，n=9÷60=15%，答：m为25%，n为15%.（2）由扇形统计图可得，   D生活应用所占百分比为：30%，∴D生活应用的人数为：60×30%=18，补全条形统计图如下，（3）解：由（1）知“数学史话”的百分比为25%，   ∴该校最喜欢“数学史话”的人数为：1200×25%=300（人）.答：该校最喜欢“数学史话”的人数为300人.20. 解：如图所示， 21.（1）如图，连结OB，设⊙O半径为r，   ∵BC与⊙O相切于点B，∴OB⊥BC，又∵四边形OABC为平行四边形，∴OA∥BC，AB=OC，∴∠AOB=90°，又∵OA=OB=r，∴AB= r，∴△AOB，△OBC均为等腰直角三角形，∴∠BOC=45°，∴弧CD度数为45°.（2）作OH⊥EF，连结OE，   由（1）知EF=AB= r，∴△OEF为等腰直角三角形，∴OH= EF= r，在Rt△OHC中，∴sin∠OCE= = ，∴∠OCE=30°.22.（1）连结PC，过 点P作PH⊥x轴于点H，如图,   ∵在正六边形ABCDEF中，点B在y轴上，∴△OBC和△PCH都是含有30°角的直角三角形，BC=PC=CD=2，∴OC=CH=1，PH= ，∴P（2， ），又∵点P在反比例函数y= 上，∴k=2 ，∴反比例函数解析式为：y= （x＞0），连结AC，过点B作BG⊥AC于点G，∵∠ABC=120°，AB=CB=2，∴BG=1，AG=CG= ，AC=2 ，∴A（1，2 ），∴点A在该反比例函数的图像上.（2）过点Q作QM⊥x轴于点M，   ∵六边形ABCDEF为正六边形，∴∠EDM=60°，设DM=b，则QM= b，∴Q（b+3， b），又∵点Q在反比例函数上，∴ b（b+3）=2 ,解得：b1= ，b2= （舍去），∴b+3= +3= ，∴点Q的横坐标为 .（3）连结AP，   ∵AP=BC=EF，AP∥BC∥EF，∴平移过程：将正六边形ABCDEF先向右平移1个单位，再向上平移 个单位，或将正六边形ABCDEF向左平移2个单位.23.（1）解：∵m=0，   ∴二次函数表达式为：y=-x2+2，画出函数图像如图1,　　　∵当x=0时，y=2；当x=1时，y=1；∴抛物线经过点（0，2）和（1，1），∴好点有：（0，0），（0，1），（0，2），（1，0）和（1，1），共5个.（2）解：∵m=3，   ∴二次函数表达式为：y=-（x-3）2+5，画出函数图像如图2,∵当x=1时，y=1；当x=2时，y=4；当x=4时，y=4；∴抛物线上存在好点，坐标分别是（1，1），（2，4）和（4，4）。（3）解：∵抛物线顶点P（m，m+2），   ∴点P在直线y=x+2上，∵点P在正方形内部，∴0＜m＜2，如图3,E（2，1），F（2，2）， ∴当顶点P在正方形OABC内，且好点恰好存在8个时，抛物线与线段EF有交点（点F除外），当抛物线经过点E（2，1）时，∴-（2-m）2+m+2=1，解得：m1= ，m2= （舍去），当抛物线经过点F（2，2）时，∴-（2-m）2+m+2=2，解得：m3=1，m4=4（舍去），∴当 ≤m＜1时，顶点P在正方形OABC内，恰好存在8个好点.24.（1）解：由旋转的性质得：   CD=CF，∠DCF=90°，∵△ABC是等腰直角三角形，AD=BD，∴∠ADO=90°，CD=BD=AD，∴∠DCF=∠ADC，在△ADO和△FCO中，∵ ，∴△ADO≌△FCO（AAS），∴DO=CO，∴BD=CD=2DO.（2）解：①如图1，分别过点D、F作DN⊥BC于点N，FM⊥BC于点M，连结BF，   ∴∠DNE=∠EMF=90°，又∵∠NDE=∠MEF，DE=EF，∴△DNE≌△EMF，∴DN=EM，又∵BD=7 ，∠ABC=45°，∴DN=EM=7，∴BM=BC-ME-EC=5，∴MF=NE=NC-EC=5，∴BF=5 ，∵点D、G分别是AB、AF的中点，∴DG= BF= ；②过点D作DH⊥BC于点H，∵AD=6BD，AB=14 ，∴BD=2 ，（ⅰ）当∠DEG=90°时，有如图2、3两种情况，设CE=t，∵∠DEF=90°，∠DEG=90°，∴点E在线段AF上，∴BH=DH=2，BE=14-t，HE=BE-BH=12-t，∵△DHE∽△ECA，∴ ，即 ，解得：t=6±2 ，∴CE=6+2 ，或CE=6-2 ，（ⅱ）当DG∥BC时，如图4,过点F作FK⊥BC于点K，延长DG交AC于点N，延长AC并截取MN=NA，连结FM，则NC=DH=2，MC=10，设GN=t，则FM=2t，BK=14-2t，∵△DHE∽△EKF，∴DH=EK=2，HE=KF=14-2t，∵MC=FK，∴14-2t=10，解得：t=2，∵GN=EC=2，GN∥EC，∴四边形GECN为平行四边形，∠ACB=90°，∴四边形GECN为矩形，∴∠EGN=90°，∴当EC=2时，有∠DGE=90°，（ⅲ）当∠EDG=90°时，如图5：过点G、F分别作AC的垂线交射线于点N、M，过点E作EK⊥FM于点K，过点D作GN的垂线交NG的延长线于点P，则PN=HC=BC-HB=12，设GN=t，则FM=2t，∴PG=PN-GN=12-t，∵△DHE∽△EKF，∴FK=2，∴CE=KM=2t-2，∴HE=HC-CE=12-（2t-2）=14-2t，∴EK=HE=14-2t，AM=AC+CM=AC+EK=14+14-2t=28-2t，∴MN= AM=14-t，NC=MN-CM=t，∴PD=t-2，∵△GPD∽△DHE，∴ ，即 ，解得：t1=10- ，t2=10+ （舍去），∴CE=2t-2=18-2 ；综上所述：CE的长为=6+2 ，6-2 ，2或18-2 .