华师版七年级数学下册第九章《多边形的内角和和外角和》 课件教案

多边形的内角和与外角和教学设计

课型：新授课             教学班级：七（2）班           授课人：郭晓兰

一、教学目的：

1.学生掌握如何求n的内角和及了解多边形的外角和大小。

2.学生能够利用n的内角和与外角和公式进行有关计算。

二、教学重点与难点：

重点：n边形的内角和与外角和定理。

难点：n边形的内角和，外角和定理的推导。

三、教学模式：

    多媒体教学

四、教学过程：

（一）复习引入

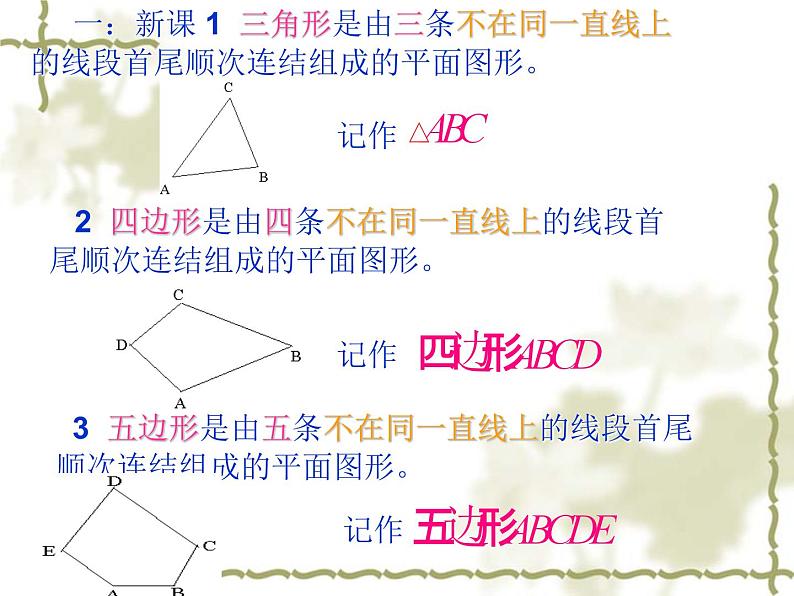
1、从五边形的一个顶点可以引______对角线，将五边形分成了______个三角形。

2、从n边形的一个顶点可以引______对角线，将n边形分成了______个三角形。

（二）探究新知

      让同学们通过探究七边形的内角和进而探究出求多边形的内角和的方法：

（1）从七边形的一个顶点向不相邻的五个顶点做两条对角线，分成五个三角形；

（2）观察发现七边形的七个内角变成了五个三角形的内角；

（3）通过计算五个三角形的内角和为900º，得到七边形的内角和为900º；

（4）通过列图标找规律的方法得出求多边形的内角和的方法。

结论：多边形的内角和公式

      n边形的内角和=(n－2) ·180°

反思：我们是通过什么方便推导出多边形的内角和的？

答：通过从多边形的一个顶点作对角线，将多边形转化为多个三角形，再通过三角形的内角和为180°，求出多边形的内角和，这就是数学里面的化归思想。

（三）例题讲解

例1:已知四边形ABCD，∠B+∠D=180°，求∠A+∠C的度数。

解:四边形的内角和为:(4-2) ×180 =360 °

∵∠B+∠D=180°

∴∠A+∠C= 360 °—(∠B+∠D)=180°

（四）深入探究

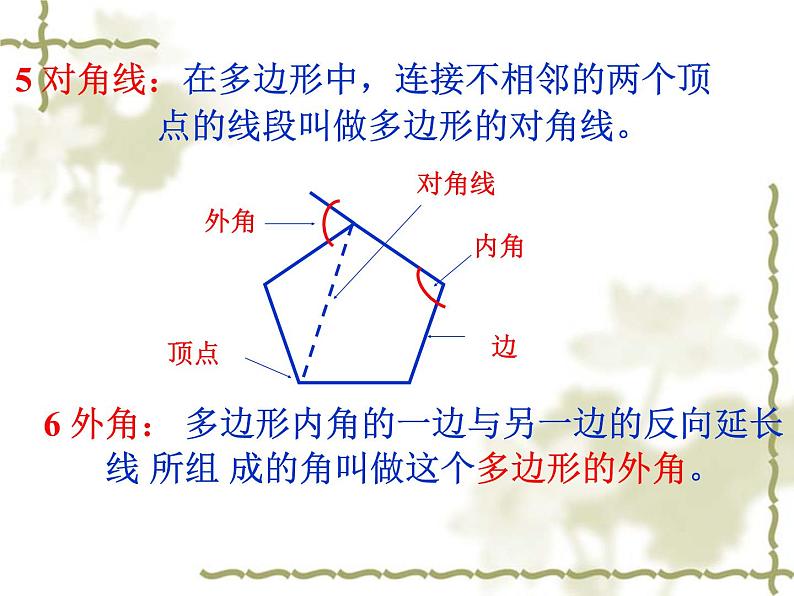
探究2： 在五边形的每个顶点处各取一个外角，这些外角的和叫做五边形的外角和．五边形的外角和等于多少？

分析：因为n边形的一个内角与它的相邻的外角互为补角，所以可先求出多边形的内角与外角的总和，再减去内角和，就可得到外角和。

n边形的内角与外角的总和为n·180°

n边形的内角和为(n-2)·180°

那么n边形的外角和为n·180°－(n－2)·180°=n·180°-n·180°+360°=360°

n边形的外角和=360°

（五）巩固练习

已知一个多边形，它的内角和是外角和的2倍，它是几边形？

解：设多边形的边数为n

∵它的内角和等于 (n-2)•180°，多边形外角和等于360º，

∴ (n-2)•180°= 720º。

 解得: n = 6

∴这个多边形的边数为6

五、课堂小结：

这节课我们通过把多边形划分成若干个三角形，用三角形内角和去求多边形的内角和，从而得到多边形的内角和公式为(n-2)·180°。这种通过从一般到特殊的转化方法，学习中须学生逐步掌握。由于多边形的外角和等于360°，所以往往在计算中利用外角和。

六、作业布置：

   教材书课后练习 第2、3题

七：课后思考题

通过九边形这个特殊的多边形试用三种不同的方法将多边形分割成三角形，并归纳总结出规律

八：课后反思：

    这节课，学生表现很积极，因为学生能在课堂上积极发言，虽然学生对多边形几乎不了解，但在教师的指导和启示下，积极思考，能够主动地、与同学之间相互交流，用自己的方式去解决问题，用于发表自己的观点，由于是新知识学生感觉很新奇。所以学生都几乎参与到整节课。效果很好