第23章 旋转章末复习 人教版九年级数学上册作业课件

这是一份第23章 旋转章末复习 人教版九年级数学上册作业课件，共12页。

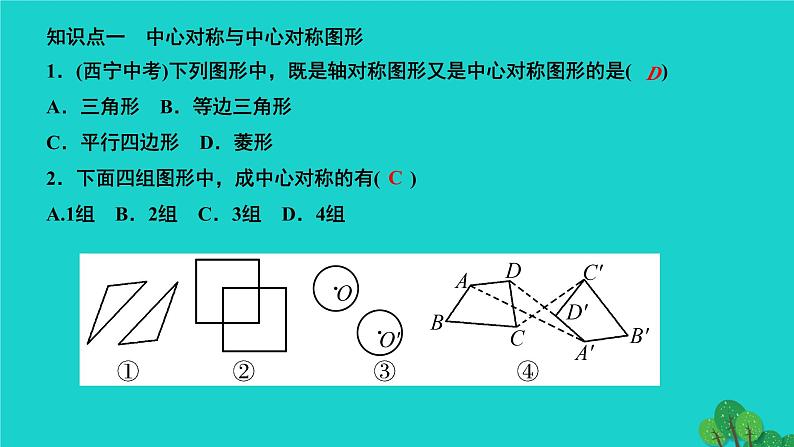
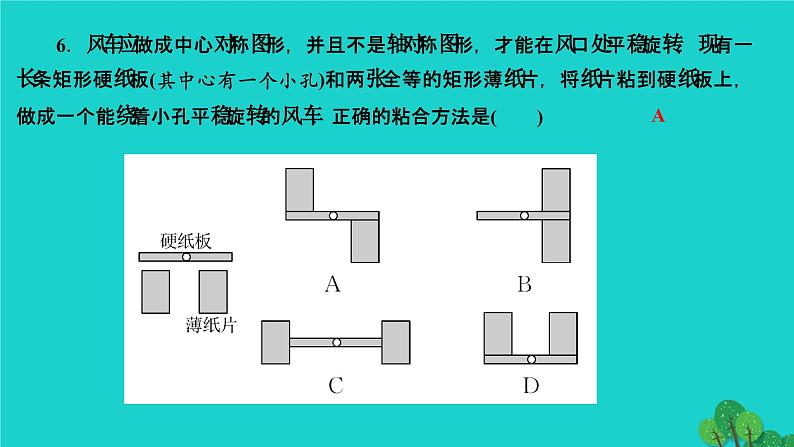
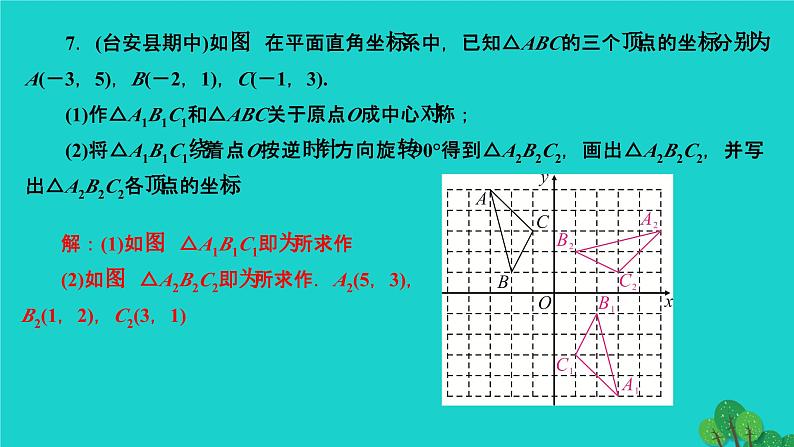
章末复习(三)　旋转第二十三章　旋转知识点一　中心对称与中心对称图形1．(西宁中考)下列图形中，既是轴对称图形又是中心对称图形的是( )A．三角形 B．等边三角形C．平行四边形 D．菱形2．下面四组图形中，成中心对称的有( )A.1组 B．2组 C．3组 D．4组DC知识点二　平面直角坐标系中的旋转及用坐标表示中心对称3．以原点为中心，将点P(4，5)按逆时针方向旋转90°，得到的点Q关于原点的对称点所在的象限为( )A．第一象限 B．第二象限C．第三象限 D．第四象限4．(滨州中考)已知点P(a－3，2－a)关于原点对称的点在第四象限，则a的取值范围在数轴上表示正确的是( )DC知识点三　图案设计问题5．如图，在方格纸上，△ABC经过变换得到△DEF，下列对变换过程的叙述正确的是( )A.绕着点A顺时针旋转90°，再向右平移7格B．向右平移4格，再向上平移7格C．绕着点A逆时针旋转90°，再向右平移7格D．向右平移4格，再绕着点A逆时针旋转90°C6．风车应做成中心对称图形，并且不是轴对称图形，才能在风口处平稳旋转．现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片，将纸片粘到硬纸板上，做成一个能绕着小孔平稳旋转的风车．正确的粘合方法是( )A7．(台安县期中)如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(－3，5)，B(－2，1)，C(－1，3).(1)作△A1B1C1和△ABC关于原点O成中心对称；(2)将△A1B1C1绕着点O按逆时针方向旋转90°得到△A2B2C2，画出△A2B2C2，并写出△A2B2C2各顶点的坐标．解：(1)如图，△A1B1C1即为所求作(2)如图，△A2B2C2即为所求作．A2(5，3)，B2(1，2)，C2(3，1)知识点四　旋转的性质及应用8．如图是一个活动的▱ABCD框架，∠ABC＝40°，拉动两个不相邻的顶点B和D，当边BA绕点B逆时针旋转α(0°＜α＜90°)时成为了矩形ABCD框架，则旋转角α的度数为( )A．40° B．50° C．60° D．90°B9．(上海中考)定义：在平面内，一个点到图形的距离是这个点到这个图上所有点的最短距离，在平面内有一个正方形，边长为2，中心为O，在正方形外有一点P，OP＝2，当正方形绕着点O旋转时，则点P到正方形的最短距离d的取值范围为 ______________．10．(衡阳中考)如图，点E为正方形ABCD外一点，∠AEB＝90°，将Rt△ABE绕点A逆时针旋转90°得到△ADF，DF的延长线交BE于点H.(1)试判定四边形AFHE的形状，并说明理由；(2)已知BH＝7，BC＝13，求DH的长．解：(1)四边形AFHE是正方形，理由如下：∵Rt△ABE绕点A逆时针旋转90°得到△ADF，∴Rt△ABE≌Rt△ADF，∴∠AEB＝∠AFD＝90°，∴∠AFH＝90°，∵Rt△ABE≌Rt△ADF，∴∠DAF＝∠BAE，又∵∠DAF＋∠FAB＝90°，∴∠BAE＋∠FAB＝90°，∴∠FAE＝90°，在四边形AFHE中，∠FAE＝90°，∠AEB＝90°，∠AFH＝90°，∴四边形AFHE是矩形，又∵AE＝AF，∴矩形AFHE是正方形；(2)设AE＝x.则由(1)以及题意可知：AE＝EH＝FH＝AF＝x，BH＝7，BC＝AB＝13，在Rt△AEB中，AB2＝AE2＋BE2，即132＝x2＋(x＋7)2，解得：x＝5，∴BE＝BH＋EH＝5＋7＝12，∴DF＝BE＝12，又∵DH＝DF＋FH，∴DH＝12＋5＝17【核心素养】11．(类比思想)如图①，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．(1)观察猜想：图①中，线段PM与PN的数量关系是____________，位置关系是______________；(2)探究证明：把△ADE绕点A按逆时针方向旋转到图②的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；(3)拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝3，AB＝7，请直接写出△PMN面积的最大值．PM＝PNPM⊥PN