



还剩13页未读,
继续阅读
数学九年级上册23.1 图形的旋转图文课件ppt
展开
这是一份数学九年级上册23.1 图形的旋转图文课件ppt,共21页。PPT课件主要包含了学习目标,新课导入,新知探究,归纳总结,根据上图填空,归纳总结旋转的性质,性质3旋转角相等,几何语言表示,课堂小结,课堂训练等内容,欢迎下载使用。
1.认识旋转这一图形变换并了解其相关概念. 2.探索并发现旋转的性质,并能利用性质证明线段相等或角相等. 3.经历从直观到抽象、从感性认识到理论认识的转变,发展直观想象能力,并体会数学美.
这些运动有什么共同的特点?
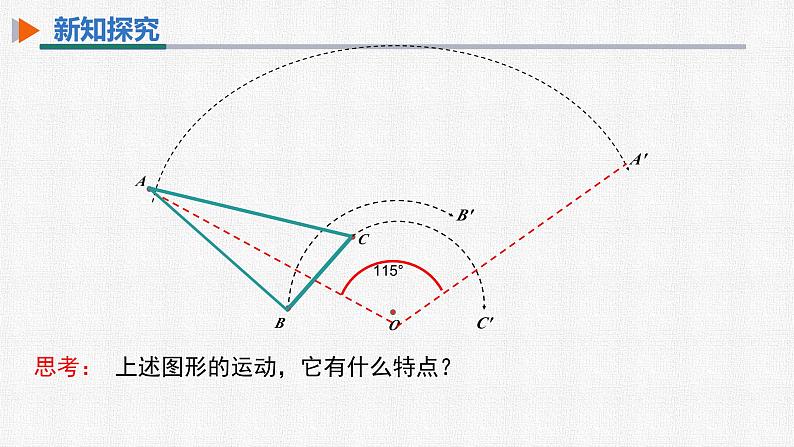
思考: 上述图形的运动,它有什么特点?
在平面内,把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转,点O叫做旋转中心,转动的角叫做旋转角.如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
转动的方向分为顺时针与逆时针.
旋转中心是点__________;图中对应点有____________________________________;图中对应线段有_____________________________________.每对对应线段的长度有怎样的关系?图中旋转角等于______.
点A与点A′,点B与点B′,点C与点C′
线段CA与C'A′、CB与C'B′、AB与A′B′
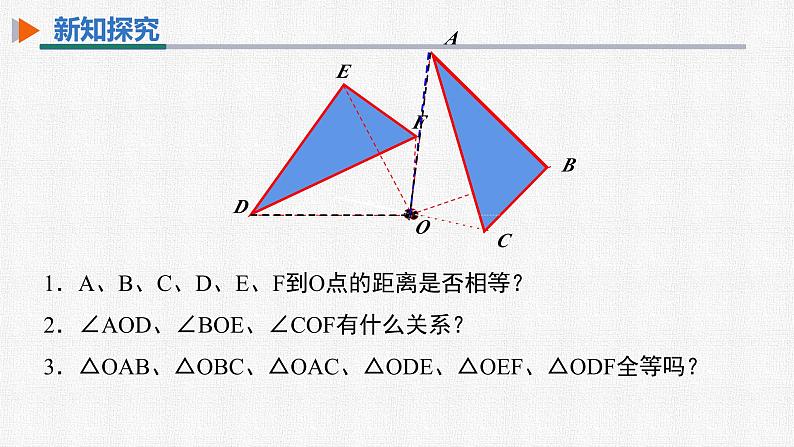
1.A、B、C、D、E、F到O点的距离是否相等?2.∠AOD、∠BOE、∠COF有什么关系?3.△OAB、△OBC、△OAC、△ODE、△OEF、△ODF全等吗?
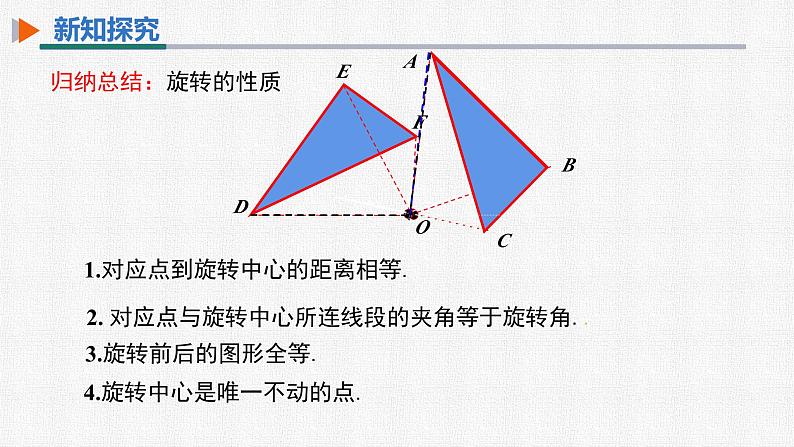
1.对应点到旋转中心的距离相等.
2. 对应点与旋转中心所连线段的夹角等于旋转角..
4.旋转中心是唯一不动的点.
3.旋转前后的图形全等.
由旋转得: ∠AOA'=∠BOB'=∠COC'
由旋转得: OA=OA' OB=OB' OC=OC'
性质2: 对应点到旋转中心的距离相等
由旋转得:△ABC ≌ △A'B'C'
性质1: 旋转前后的图形全等
思考:借助上图,如何确定它们的旋转中心位置?
找到两条对应点连线段的垂直平分线的交点.
例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等, 所以∠ABE′=∠ADE=90°, BE′=DE .
解:因为点A是旋转中心,所以它的对应点是它本身.
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
因此,在CB的延长线上取点E′,使BE′=DE,则△ABE′为旋转后的图形.
例2 如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别交于点E,F.求证:△BCF≌△BA1D;
证明:∵△ABC是等腰三角形, ∴AB=BC,∠A=∠C, 由旋转的性质,可得 A1B=AB=BC, ∠A=∠A1=∠C,∠A1BD=∠CBC1, 在△BCF与△BA1D中,
△BCF≌△BA1D;
三要素:旋转中心,旋转方向和旋转角度
1.对应点到旋转中心的距离相等. 2. 对应点与旋转中心所连线段的夹角等于旋转角. 3.旋转前后的图形全等. 4.旋转中心是唯一不动的点.
1.下列现象中属于旋转的有( )个①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.A.2 B.3 C.4 D.5
2.△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( ) A.DE=3 B.AE=4 C.∠CAB是旋转角 D.∠CAE是旋转角
A.30°B.45°C.90°D.135°
3.如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
4.如图,在平面直角坐标系中,Rt△OAB的顶点A的坐标为( ,1) ∠AOB= 30°,若将△OAB绕O点逆时针旋转60度后,A点到达C点,则C点的坐标是 ______.
5.如图,△ABC是等边三角形,△APC逆时针旋转后能与△AP′B重合.连结PP ′,则△APP ′是 _____三角形; 若AP=6,BP=8,PC=10,则∠APB=_____.
1.认识旋转这一图形变换并了解其相关概念. 2.探索并发现旋转的性质,并能利用性质证明线段相等或角相等. 3.经历从直观到抽象、从感性认识到理论认识的转变,发展直观想象能力,并体会数学美.
这些运动有什么共同的特点?
思考: 上述图形的运动,它有什么特点?
在平面内,把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转,点O叫做旋转中心,转动的角叫做旋转角.如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
转动的方向分为顺时针与逆时针.
旋转中心是点__________;图中对应点有____________________________________;图中对应线段有_____________________________________.每对对应线段的长度有怎样的关系?图中旋转角等于______.
点A与点A′,点B与点B′,点C与点C′
线段CA与C'A′、CB与C'B′、AB与A′B′
1.A、B、C、D、E、F到O点的距离是否相等?2.∠AOD、∠BOE、∠COF有什么关系?3.△OAB、△OBC、△OAC、△ODE、△OEF、△ODF全等吗?
1.对应点到旋转中心的距离相等.
2. 对应点与旋转中心所连线段的夹角等于旋转角..
4.旋转中心是唯一不动的点.
3.旋转前后的图形全等.
由旋转得: ∠AOA'=∠BOB'=∠COC'
由旋转得: OA=OA' OB=OB' OC=OC'
性质2: 对应点到旋转中心的距离相等
由旋转得:△ABC ≌ △A'B'C'
性质1: 旋转前后的图形全等
思考:借助上图,如何确定它们的旋转中心位置?
找到两条对应点连线段的垂直平分线的交点.
例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等, 所以∠ABE′=∠ADE=90°, BE′=DE .
解:因为点A是旋转中心,所以它的对应点是它本身.
在正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
因此,在CB的延长线上取点E′,使BE′=DE,则△ABE′为旋转后的图形.
例2 如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别交于点E,F.求证:△BCF≌△BA1D;
证明:∵△ABC是等腰三角形, ∴AB=BC,∠A=∠C, 由旋转的性质,可得 A1B=AB=BC, ∠A=∠A1=∠C,∠A1BD=∠CBC1, 在△BCF与△BA1D中,
△BCF≌△BA1D;
三要素:旋转中心,旋转方向和旋转角度
1.对应点到旋转中心的距离相等. 2. 对应点与旋转中心所连线段的夹角等于旋转角. 3.旋转前后的图形全等. 4.旋转中心是唯一不动的点.
1.下列现象中属于旋转的有( )个①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.A.2 B.3 C.4 D.5
2.△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( ) A.DE=3 B.AE=4 C.∠CAB是旋转角 D.∠CAE是旋转角
A.30°B.45°C.90°D.135°
3.如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
4.如图,在平面直角坐标系中,Rt△OAB的顶点A的坐标为( ,1) ∠AOB= 30°,若将△OAB绕O点逆时针旋转60度后,A点到达C点,则C点的坐标是 ______.
5.如图,△ABC是等边三角形,△APC逆时针旋转后能与△AP′B重合.连结PP ′,则△APP ′是 _____三角形; 若AP=6,BP=8,PC=10,则∠APB=_____.














