初中苏科版2.1 圆课堂检测

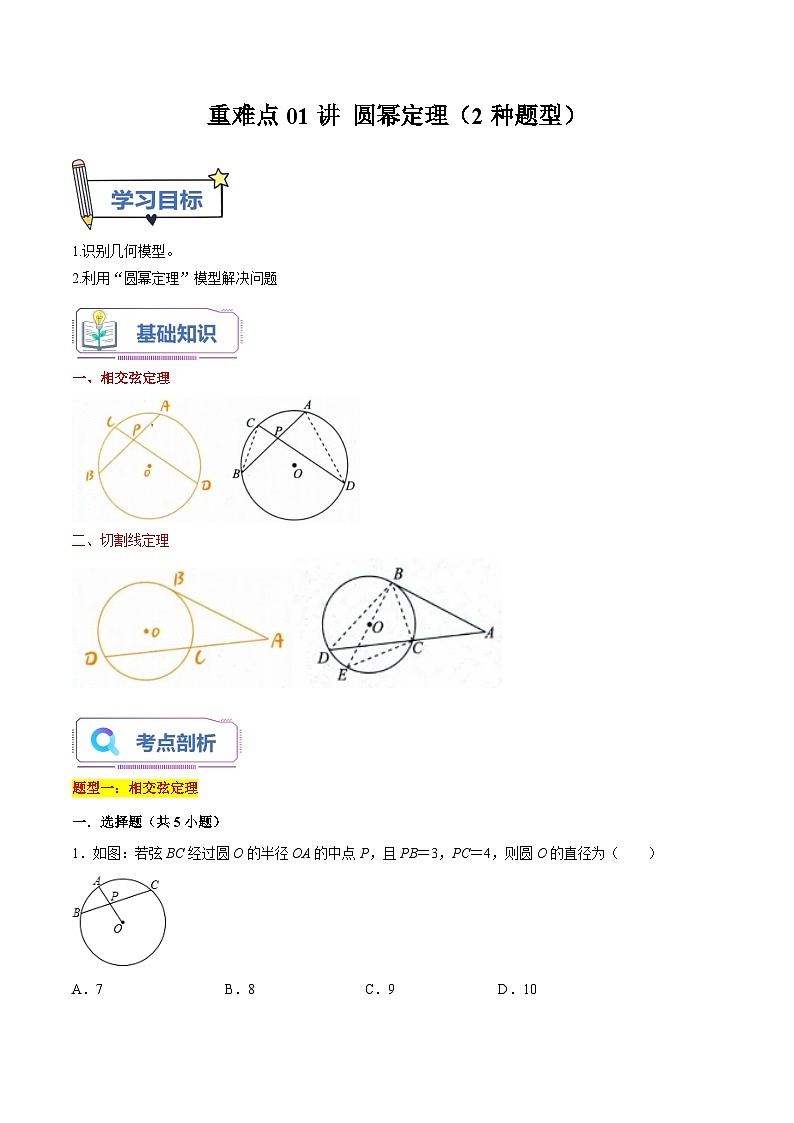
重难点01讲 圆幂定理（2种题型）

1.识别几何模型。

2.利用“圆幂定理”模型解决问题

一、相交弦定理

二、切割线定理

题型一：相交弦定理

一．选择题（共5小题）

1．如图：若弦BC经过圆O的半径OA的中点P，且PB＝3，PC＝4，则圆O的直径为（　　）

A．7 B．8 C．9 D．10

2．如图，⊙O的直径AB垂直弦CD于P，且P是半径OB的中点，CD＝6cm，则直径AB的长是（　　）

A．2cm B．3cm C．4cm D．4cm

3．如图，⊙O中，弦AB和CD相交于P，CP＝2.5，PD＝6，AB＝8，那么以AP、PB的长为两根的一元二次方程是（　　）

A．x2﹣8x﹣15＝0 B．x2﹣8x+15＝0 C．x2+8x﹣15＝0 D．x2+8x+15＝0

4．如图，已知⊙O的弦AB、CD相交于点P，PA＝4cm，PB＝3cm，PC＝6cm，EA切⊙O于点A，AE与CD的延长线交于点E，若AE＝cm，则PE的长为（　　）

A．4cm B．3cm C．5cm D．cm

5．如图点P为弦AB上一点，连接OP，过P作PC⊥OP，PC交⊙O于点C，若AP＝4，PB＝2，则PC的长为（　　）

A． B．2 C． D．3

二．填空题（共8小题）

6．已知如图，等腰△ABC内接于⊙O，∠B＝∠ACB＝30°，弦AD交BC于E，AE＝2，ED＝4，则⊙O的半径为　   　．

7．工程上常用钢珠来测量零件上小孔的直径，假设钢珠的直径是10mm，测得钢珠顶端离零件表面的距离为8mm，如图所示，则这个小孔的直径AB是　  　mm．

8．如图，四边形ABCD是⊙O的内接矩形，AB＝2，BC＝4，E是BC的中点，AE的延长线交⊙O于点F，则EF的长是　   　．

9．如图，⊙O过M点，⊙M交⊙O于A，延长⊙O的直径AB交⊙M于C，若AB＝8，BC＝1，则AM＝　　．

10．善于归纳和总结的小明发现，“数形结合”是初中数学的基本思想方法，被广泛地应用在数学学习和解决问题中．用数量关系描述图形性质和用图形描述数量关系，往往会有新的发现．小明在研究垂直于直径的弦的性质过程中（如图，直径AB⊥弦CD于E），设AE＝x，BE＝y，他用含x，y的式子表示图中的弦CD的长度，通过比较运动的弦CD和与之垂直的直径AB的大小关系，发现了一个关于正数x，y的不等式，你也能发现这个不等式吗？写出你发现的不等式　            　．

11．如图，AB是⊙O的直径，弦CD⊥AB，垂足是G，F是CG的中点，延长AF交⊙O于E，CF＝2，AF＝3，则EF的长是　　．

12．已知：如图，PT切⊙O于点T，PA交⊙O于A，B两点且与直径CT交于点D，CD＝2，AD＝3，BD＝6，则PB＝　　．

13．如图，正方形ABCD内接于⊙O，E为DC的中点，直线BE交⊙O于点F，如果⊙O的半径为，则O点到BE的距离OM＝　　．

三．解答题（共2小题）

14．如图，⊙O中，直径CD⊥弦AB于E点，若CD＝10，DE＝2，求AB的长．

15．如图，⊙O的直径AB＝10，弦DE⊥AB于点H，AH＝2．

（1）求DE的长；

（2）延长ED到P，过P作⊙O的切线，切点为C，若PC＝2，求PD的长．

题型二、切割线定理

一．选择题（共5小题）

1．已知：如图⊙O的割线PAB交⊙O于点A，B，PA＝7cm，AB＝5cm，PO＝10cm，则⊙O的半径是（　　）

A．4cm B．5cm C．6cm D．7cm

2．如图：PAB、PCD为⊙O的两条割线，若PA•PB＝30，PC＝3，则CD的长为（　　）

A．10 B．7 C． D．3

3．如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B、C两点，PB＝2cm，BC＝8cm，则PA的长等于（　　）

A．4cm B．16cm C．20cm D．2cm

4．如图，在Rt△ABC中，AC＝5，BC＝12，⊙O分别与边AB，AC相切，切点分别为E，C，则⊙O的半径是（　　）

A． B． C． D．

5．如图，PA是⊙O的切线，A为切点，PBC是过点O的割线．若PA＝8cm，PB＝4cm，则⊙O的直径为（　　）

A．6cm B．8cm C．12cm D．16cm

二．填空题（共3小题）

6．如图，PA切⊙O于点A，PBC是⊙O的割线，若PB＝BC＝2，则PA＝　　．

7．如图，已知Rt△ABC的两条直角边AC，BC的长分别为3，4，以AC为直径作圆与斜边AB交于点D，则AD＝　　．

8．如图，已知Rt△ABC中，∠C＝90°，AC＝，BC＝1，若以C为圆心，CB为半径的圆交AB于点P，则AP＝　　．

三．解答题（共4小题）

9．如图，AB是⊙O的直径，点C是BA延长线上一点，CD切⊙O于D点，弦DE∥CB，Q是AB上一动点，CA＝1，CD是⊙O半径的倍．

（1）求⊙O的半径R；

（2）当Q从A向B运动的过程中，图中阴影部分的面积是否发生变化？若发生变化，请你说明理由；若不发生变化，请你求出阴影部分的面积．

10．如图，⊙O的直径AB＝10，弦DE⊥AB于点H，AH＝2．

（1）求DE的长；

（2）延长ED到P，过P作⊙O的切线，切点为C，若PC＝2，求PD的长．

11．如图，在△ABC中，∠BAC＝90度．BM平分∠ABC交AC于M，以A为圆心，AM为半径作⊙A交BM于N，AN的延长线交BC于D，直线AB交⊙A于P，K两点，作MT⊥BC于T．

（1）求证：AK＝MT；

（2）求证：AD⊥BC；

（3）当AK＝BD时，求证：．

12．如图，AB是⊙O的直径，CB、CE分别切⊙O于点B、D，CE与BA的延长线交于点E，连接OC、OD．

（1）△OBC与△ODC是否全等？　　（填“是”或“否”）；

（2）已知DE＝a，AE＝b，BC＝c，请你思考后，选用以上适当的数，设计出计算⊙O半径r的一种方案：

①你选用的已知数是　            　；

②写出求解过程．（结果用字母表示）

一．选择题（共2小题）

1．（2022秋•武汉期中）如图，已知AB是⊙O的一条弦，直径CD与弦AB交于点E，且BE＝3AE，已知DE＝8，CE＝2，则点O到AB的距离为（　　）

A． B． C．2 D．

2．（2021•涟源市三模）如图，⊙O上经过点A的切线交直径CB的延长线于点P，且∠C＝30°，⊙O的半径为2，则下列结论错误的是（　　）

A．的长为 B．△ABP为等腰三角形 

C．B为OP中点 D．∠P＝30°

二．解答题（共2小题）

3．（2020•青秀区校级三模）如图，以△ABC的一边BC为直径的⊙O，交AB于点D，连接CD，OD，已知∠A+∠1＝90°．

（1）求证：AC是⊙O的切线；

（2）若∠B＝30°，AD＝2，求⊙O的半径．

4．（2023•郸城县一模）请阅读以下材料，完成相应任务．

我们知道，过任意一个三角形的三个顶点能作一个圆，那么过任意一个四边形的四个顶点能作一个圆吗？李雷经过实践探究发现了如下结论：

如果线段同侧两点（与线段在同一平面内）分别与线段两端点的连线所组成的夹角相等，那么这两点和线段两端点四点共圆．下面是李雷证明上述命题的过程（不完整）．

已知：如图1，点C，D是线段AB同侧两点，且∠ACB＝∠ADB．

求证：点A，B，C，D四点共圆．

证明：作△ABC的外接圆⊙O，假设点D在⊙O外或在⊙O内．

如图2，若点D在⊙O外．设AD与⊙O交于点E，连接BE，

则∠ACB＝∠AEB（依据一），

又∵∠AEB＝∠ADB+∠DBE（依据二），

∴∠ACB＝∠ADB+∠DBE．

∴∠ACB＞∠ADB．这与已知条件“∠ACB＝∠ADB”矛盾，故点D在⊙O外不成立；

如图3，若点D在⊙O内，……

（请同学们补充完整省略的部分证明过程）

综上所述，作△ABC的外接圆⊙O，点D在⊙O上，即点A，B，C，D四点共圆．

（1）填空：将材料中依据一、依据二补充完整；

依据一：　同弧所对的圆周角相等　；

依据二：　三角形的外角等于与它不相邻的两个内角的和　．

（2）请按照上面的证明思路，写出该证明的剩余部分；

（3）填空：如图4，在四边形ABCD中，∠ABD＝∠ACD，对角线AC，BD交于点E，E为AC中点，若BD＝6，BE＝4，则AC＝　4　．