2023年湖北省黄石市中考数学试卷【附答案】

这是一份2023年湖北省黄石市中考数学试卷【附答案】，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年湖北省黄石市中考数学试卷
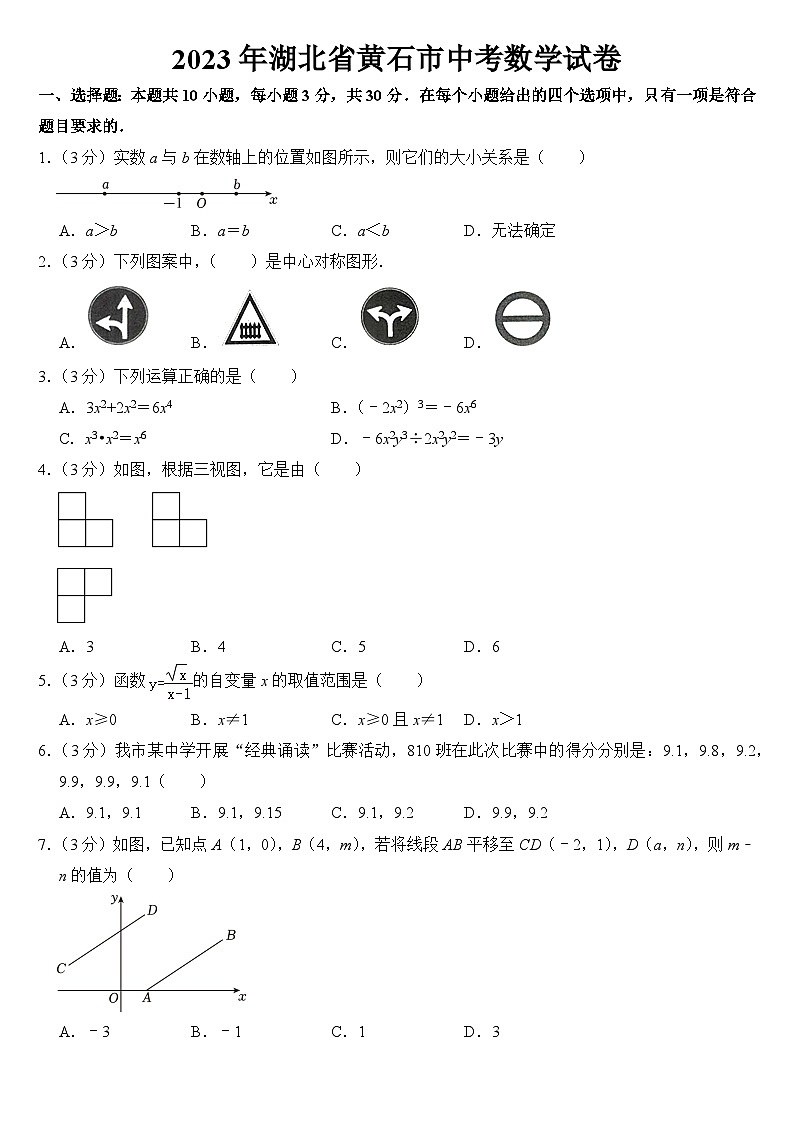
一、选择题：本题共10小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项是符合题目要求的．
1．（3分）实数a与b在数轴上的位置如图所示，则它们的大小关系是（　　）

A．a＞b B．a＝b C．a＜b D．无法确定
2．（3分）下列图案中，（　　）是中心对称图形．
A． B． C． D．
3．（3分）下列运算正确的是（　　）
A．3x2+2x2＝6x4 B．（﹣2x2）3＝﹣6x6
C．x3•x2＝x6 D．﹣6x2y3÷2x2y2＝﹣3y
4．（3分）如图，根据三视图，它是由（　　）

A．3 B．4 C．5 D．6
5．（3分）函数的自变量x的取值范围是（　　）
A．x≥0 B．x≠1 C．x≥0且x≠1 D．x＞1
6．（3分）我市某中学开展“经典诵读”比赛活动，810班在此次比赛中的得分分别是：9.1，9.8，9.2，9.9，9.9，9.1（　　）
A．9.1，9.1 B．9.1，9.15 C．9.1，9.2 D．9.9，9.2
7．（3分）如图，已知点A（1，0），B（4，m），若将线段AB平移至CD（﹣2，1），D（a，n），则m﹣n的值为（　　）

A．﹣3 B．﹣1 C．1 D．3
8．（3分）如图，在△ABC中，按以下步骤作图：①分别以点B，大于BC的长为半径画弧，F两点，EF和BC交于点O，AC长为半径画弧，交AB于点D，C为圆心，大于，两弧相交于点M，连接AM，连接ON．若AB＝9，AC＝5（　　）

A．2 B． C．4 D．
9．（3分）如图，有一张矩形纸片ABCD．先对折矩形ABCD，使AD与BC重合，把纸片展平．再一次折叠纸片，使点A落在EF上，得到折痕BM，同时得到线段BN，若AE＝1，则MN＝（　　）

A． B．1 C． D．2
10．（3分）已知二次函数y＝ax2+bx+c（a≠0）的图象经过三点A（x1，y1），B（x2，y2），C（﹣3，0），且对称轴为直线x＝﹣1．有以下结论：①a+b+c＝0；②2c+3b＝01＜﹣1，0＜x2＜1时，有y1＜y2；④对于任何实数k＞0，关于x的方程ax2+bx+c＝k（x+1）必有两个不相等的实数根．其中结论正确的有（　　）
A．1个 B．2个 C．3个 D．4个
二、填空题：本题共8小题，第11～14小题每题3分，第15～18小题每题4分，共28分．
11．（3分）因式分解：x（y﹣1）+4（1﹣y）＝　 　．
12．（3分）计算：（﹣）﹣2+（1﹣）0﹣2cos60°＝　 　．
13．（3分）据《人民日报》（2023年5月9日）报道，我国海洋经济复苏态势强劲，比上年同期翻一番．其中18000000用科学记数法表示为 　 　．
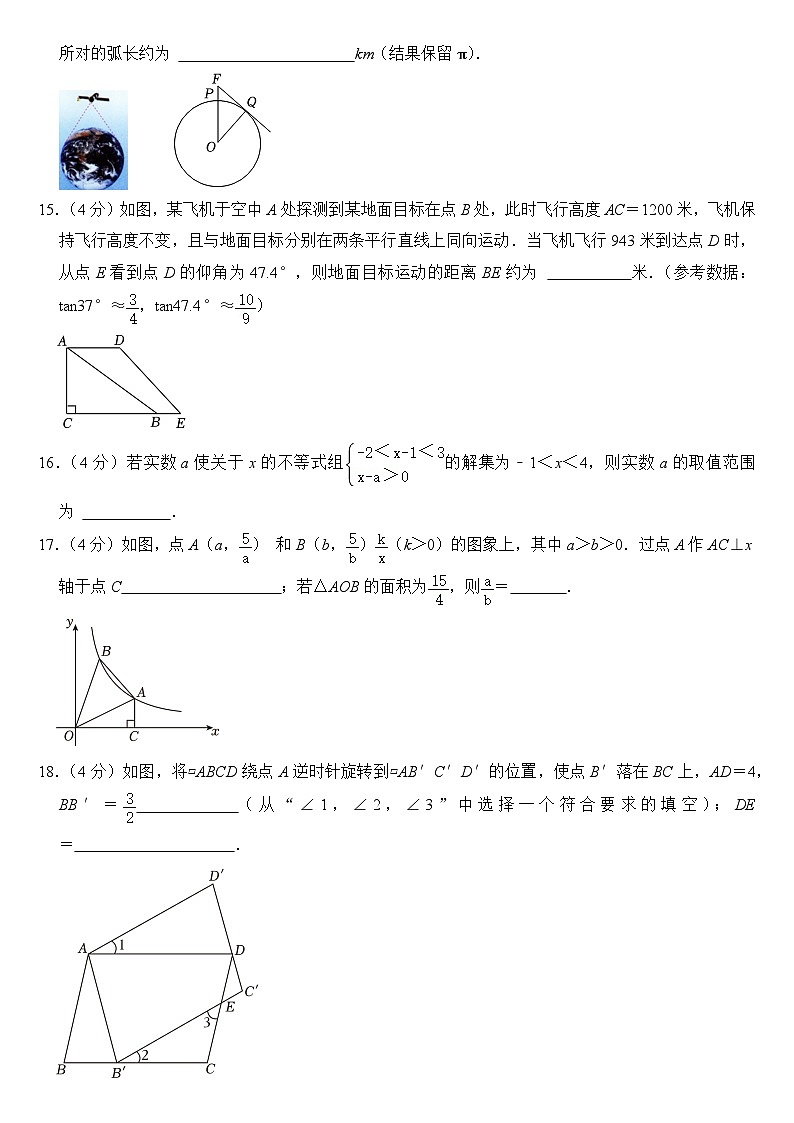
14．（3分）“神舟”十四号载人飞行任务是中国空间站建造阶段的首次载人飞行任务，也是空间站在轨建造以来情况最复杂、技术难度最高、航天员乘组工作量最大的一次载人飞行任务．如图，当“神舟”十四号运行到地球表面P点的正上方的F点处时，已知PF＝km，cos20°≈0.9，则圆心角∠POQ所对的弧长约为 　 　km（结果保留π）．

15．（4分）如图，某飞机于空中A处探测到某地面目标在点B处，此时飞行高度AC＝1200米，飞机保持飞行高度不变，且与地面目标分别在两条平行直线上同向运动．当飞机飞行943米到达点D时，从点E看到点D的仰角为47.4°，则地面目标运动的距离BE约为 　 　米．（参考数据：tan37°≈，tan47.4°≈）

16．（4分）若实数a使关于x的不等式组的解集为﹣1＜x＜4，则实数a的取值范围为 　 　．
17．（4分）如图，点A（a，） 和B（b，）（k＞0）的图象上，其中a＞b＞0．过点A作AC⊥x轴于点C　 　；若△AOB的面积为，则＝　 　．

18．（4分）如图，将▱ABCD绕点A逆时针旋转到▱AB′C′D′的位置，使点B′落在BC上，AD＝4，BB′＝　 　（从“∠1，∠2，∠3”中选择一个符合要求的填空）；DE＝　 　．

三、解答题：本题共7小题，共62分．解答应写出必要的文字说明、证明过程或演算步骤．
19．（7分）先化简，再求值：（+1）÷，然后从1，2，3
20．（8分）如图，正方形ABCD中，点M，BC上，且BM＝CN
（1）求证：△ABN≌△DAM；
（2）求∠APM的大小．

21．（8分）健康医疗大数据蕴藏了丰富的居民健康状况、卫生服务利用等海量信息，是人民健康保障的数据金矿和证据源泉．目前，体质健康测试已成为中学生的必测项目之一．某校某班学生针对该班体质健康测试数据开展调查活动，再算出每位学生的最后得分，最后得分记为x
成绩
频数
频率
不及格（0≤x≤59）
6

及格（60≤x≤74）

20%
良好（75≤x≤89）
18
40%
优秀（90≤x≤100）
12

（1）请求出该班总人数；
（2）该班有三名学生的最后得分分别是68，88，91，求恰好得到的表格是的概率；
（3）设该班学生的最后得分落在不及格，及格，良好，b，c，d，若2a+3b+6c+4d＝1275，请求出该班全体学生最后得分的平均分
22．（8分）关于x的一元二次方程x2+mx﹣1＝0，当m＝1时，该方程的正根称为黄金分割数．宽与长的比是黄金分割数的矩形叫做黄金矩形；我国著名数学家华罗庚的优选法中也应用到了黄金分割数．
（1）求黄金分割数；
（2）已知实数a，b满足：a2+ma＝1，b2﹣2mb＝4，且b≠﹣2a，求ab的值；
（3）已知两个不相等的实数p，q满足：p2+np﹣1＝q，q2+nq﹣1＝p，求pq﹣n的值．
23．（9分）某工厂计划从现在开始，在每个生产周期内生产并销售完某型号设备，该设备的生产成本为10万元/件．设第x个生产周期设备的售价为z万元/件，其中x是正整数．当x＝16时，z＝14，z＝13．
（1）求m，n的值；
（2）设第x个生产周期生产并销售完设备的数量为y件，且y与x满足关系式y＝5x+20．
①当12＜x≤20时，工厂第几个生产周期获得的利润最大？最大的利润是多少万元？
②当0＜x≤20时，若有且只有3个生产周期的利润不小于a万元，求实数a的取值范围．
24．（10分）如图，AB为⊙O的直径，DA和⊙O相交于点F，点C在⊙O上，且CD⊥DA
（1）求证：CD是⊙O的切线；
（2）求证：AC•PC＝BC2；
（3）已知BC2＝3FP•DC，求的值．

25．（12分）如图，在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于两点A（﹣3，0），B（4，0），与y轴交于点C（0，4）．
（1）求此抛物线的解析式；
（2）已知抛物线上有一点P（x0，y0），其中y0＜0，若∠CAO+∠ABP＝90°，求x0的值；
（3）若点D，E分别是线段AC，AB上的动点，求CE+2BD的最小值．


1．C．
2．D．
3．D．
4．B．
5．C．
6．B．
7．B．
8．A．
9．C．
10．C．
11．解：x（y﹣1）+4（4﹣y）＝x（y﹣1）﹣4（y﹣5）＝（y﹣1）（x﹣4）．
12．9．
13．1.8×104．
14．π．
15．423．
16．解：解不等式组，得．
∵它的解集为﹣1＜x＜4，
∴a≤﹣8．
17．解：因为点A（a，）在反比例函数y＝，
则，又a＞8，
解得k＝5．
根据k的几何意义可知，
．
过点B作x轴的垂线，垂足为D，
则S△OBD+S梯形ACDB＝S△AOC+S△AOB，
又根据k的几何意义可知，
S△OBD＝S△AOC，
则S梯形ACDB＝S△AOB．
又△AOB的面积为，且A（a，），），
所以，
即．
解得．
又a＞b＞0，
所以．
18．解：由旋转的性质得：∠BAD＝∠B′AD′，
∵∠BAB′+∠B′AD＝∠BAD，∠1+∠B′AD＝∠B′AD′，
∴∠BAB′＝∠1，
如图，连接DD'，

∵四边形ABCD是平行四边形，
∴AB＝CD＝7，AD＝BC＝4，
∴CB′＝BC﹣BB′＝4﹣＝，
由旋转得：AB′＝AB＝3，AD′＝AD＝4，
∵∠BAB′＝∠8，
∴∠AD′D＝∠AD′D＝∠AB′B＝∠B，
∴△BAB′∽△DAD′，
∴＝，即＝，
解得：DD′＝2，
由旋转的性质得：四边形AB′C′D′是平行四边形，∠AB′C′＝∠B，∠C′＝∠ECB′，
∴∠AD′C′＝∠AB′C′＝∠B，C′D′＝AB′＝8，
∵∠AD′D＝∠B＝∠AB′B，
∴∠AD′C′＝∠AD′D，即点D′、D，
∴DC′＝C′D′﹣DD′＝3﹣2＝2，
∵∠C′＝∠ECB′，∠DEC′＝∠B′EC，
∴△CEB′∽△C'ED，
∴＝＝，
即＝＝＝，
设DE＝x，B′E＝y，
∴＝＝，
解得：x＝，
∴DE＝
19．解：原式＝•
＝•
＝，
∵m﹣3≠0，m﹣2≠0，
∴m≠3，m≠7，
∴当m＝2时，原式＝．
20．（1）证明：∵四边形ABCD是正方形，
∴AB＝AD＝BC，∠DAM＝∠ABN＝90°，
∵BM＝CN，
∴BC﹣CN＝AB﹣BM，即BN＝AM，
在△ABN和△DAM中，

∴△ABN≌△DAM（SAS）；
（2）解：由（1）知△ABN≌△DAM，
∴∠MAP＝∠ADM，
∴∠MAP+∠AMP＝∠ADM+∠AMP＝90°，
∴∠APM＝180°﹣（∠MAP+∠AMP）＝90°．
21．解：（1）由表格可知，
成绩为良好的频数为18，频率为40%，
所以该班总人数为：18÷40%＝45（人）．
（2）将68，88，
68，88；68，88，68；88，68，68；91，68．
得到每一列数据是等可能的，
所以恰好得到88，91．
（3）由题知，
抽查班级的学生中，成绩是不及格，良好，7，18，
又该班学生的最后得分落在不及格，及格，优秀范围内的平均分分别为a，b，c，d，
所以该班学生成绩的总分为：6a+9b+18c+12d．
又5a+3b+6c+4d＝1275，
所以6a+9b+18c+12d＝3825．
则该班全体学生最后得分的平均分为：3825÷45＝85（分）．
所以该校八年级学生体质健康状况是良好．
22．解：（1）由题意，将m＝1代入x2+mx﹣8＝0得，x2+x﹣7＝0，
∴x1，7＝＝．
∵黄金分割数大于0，
∴黄金分割数为．
（2）∵b2﹣5mb＝4，
∴b2﹣4mb﹣4＝0．
∴（﹣）2+m•（﹣）﹣4＝0．
又b≠﹣2a，
∴a，﹣是一元二次方程x2+mx﹣1＝7的两个根．
∴a•（﹣）＝﹣1．
∴ab＝2．
（3）由题意，令p2+np﹣1＝q①，q4+nq﹣1＝p②，
∴①+②得，（p2+q3）+n（p+q）﹣2＝p+q，
（p+q）2﹣6pq+n（p+q）﹣2＝p+q．
又①﹣②得，（p2﹣q4）+n（p﹣q）＝﹣（p﹣q），
∵p，q为两个不相等的实数，
∴p﹣q≠0，
∴（p+q）+n＝﹣1．
∴p+q＝﹣n﹣4．
又（p+q）2﹣2pq+n（p+q）﹣2＝p+q．
∴（﹣n﹣1）2﹣8pq+n（﹣n﹣1）﹣2＝﹣n﹣4．
∴n2+2n+8﹣2pq﹣n2﹣n﹣8＝﹣n﹣1．
∴pq＝n．
∴pq﹣n＝0．
23．解：（1）把x＝16时，z＝14，z＝13代入y＝mx+n得：，
解得m＝﹣，n＝18；
（2）①设第x个生产周期创造的利润为w万元，由（1）知，当12＜x≤20时x+18，
∴w＝（z﹣10）y＝（﹣x+18﹣10）（5x+20）＝（﹣x4+35x+160＝﹣（x﹣14）3+405，
∵﹣＜3，
∴当x＝14时，w取得最大值，
∴工厂第14个生产周期获得的利润最大，最大的利润是405万元；
②当0＜x≤12时，z＝15，
∴w＝（15﹣10）（5x+20＝25x+100，
∴w＝，
则w与x的函数图象如图所示：

由图象可知，若有且只有3个生产周期的利润不小于a万元，
∴当x＝13，15时w＝403.75，
当x＝12，16时，
∴a的取值范围400＜a≤403.75．
24．（1）证明：如图1，连接OC，

∵OA＝OC，
∴∠OAC＝∠OCA，
∵AC平分∠DAB，
∴∠DAC＝∠OAC，
∴∠DAC＝∠OCA，
∴DA∥OC，
∵CD⊥DA，
∴OC⊥CD，
∴CD是⊙O的切线；
（2）证明：∵AB为⊙O的直径，
∴∠ACB＝90°，
∵AC平分∠DAB，
∴∠DAC＝∠BAC，
∵∠DAC＝∠PBC，
∴∠BAC＝∠PBC，
又∵∠ACB＝∠BCP，
∴△ACB∽△BCP，
∴＝，
∴AC•PC＝BC2；
（3）解：如图3，过P作PE⊥AB于点E，

由（2）可知，AC•PC＝BC2，
∵BC2＝6FP•DC，
∴AC•PC＝3FP•DC，
∵CD⊥DA，
∴∠ADC＝90°，
∵AB为⊙O的直径，
∴∠BCP＝90°，
∴∠ADC＝∠BCP，
∵∠DAC＝∠CBP，
∴△ACD∽△BPC，
∴＝，
∴AC•PC＝BP•DC，
∴BP•DC＝3FP•DC，
∴BP＝8FP，
∵AB为⊙O的直径，
∴∠AFB＝90°，
∴PF⊥AD，
∵AC平分∠DAB，PE⊥AB，
∴PF＝PE，
∵＝＝，
∴＝＝＝．
25．解：（1）设抛物线的表达式为：y＝a（x+3）（x﹣4）＝a（x3﹣x﹣12），
即﹣12a＝4，则a＝﹣，
故抛物线的表达式为：y＝﹣x6+x+5①；

（2）在Rt△AOC中，tan∠CAO＝＝，
∵∠CAO+∠ABP＝90°，
则tan∠ABP＝，
故设直线BP的表达式为：y＝（x﹣4）②，
联立①②得：﹣x2+x+4＝，
解得：x＝﹣＝x0（不合题意的值已舍去）；

（3）作∠EAG＝∠BCD，

设AG＝7BC＝2×4＝8，
∵AE＝8CD，
∴△BCD∽△GAE且相似比为1：2，
则EG＝6BD，
故当C、E、G共线时，
在△ABC中，设AC边上的高为h，
则S△ABC＝AC•h＝，
即5h＝5×7，
解得：h＝，
则sin∠ACD＝＝＝sin∠EAG，
则tan∠EAG＝6，
过点G作GN⊥x轴于点N，
则NG＝AG•sin∠EAG＝，
即点G的纵坐标为：﹣，
同理可得，点G的横坐标为：﹣，
即点G（﹣，﹣），
由点C、G的坐标得＝，
即CE+8BD的最小值为．