浙教版初中数学八年级上册第五章《一次函数》单元测试卷（含答案解析）（标准困难）

这是一份浙教版初中数学八年级上册第五章《一次函数》单元测试卷（含答案解析）（标准困难），共17页。
浙教版初中数学八年级上册第五章《一次函数》单元测试卷（含答案解析）（标准困难）考试范围：第五章 考试时间 ：120分钟  总分 ：120分第I卷（选择题）一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）1.  下列变量间的关系，不是函数关系的是(    )A. 长方形的宽一定，其长与面积 B. 正方形的面积与周长
C. 等腰三角形的面积与底边长 D. 圆的周长与半径2.  某项目化学习小组的同学在水中掺入酒精，充分混合后，放入冰箱冷冻室根据实验数据作出混合液温度随时间变化而变化的图象下列说法不正确的是(    )
A. 在这个变化过程中，自变量是时间，因变量是混合液的温度
B. 混合液的温度随着时间的增大而下降
C. 当时间为时，混合液的温度为
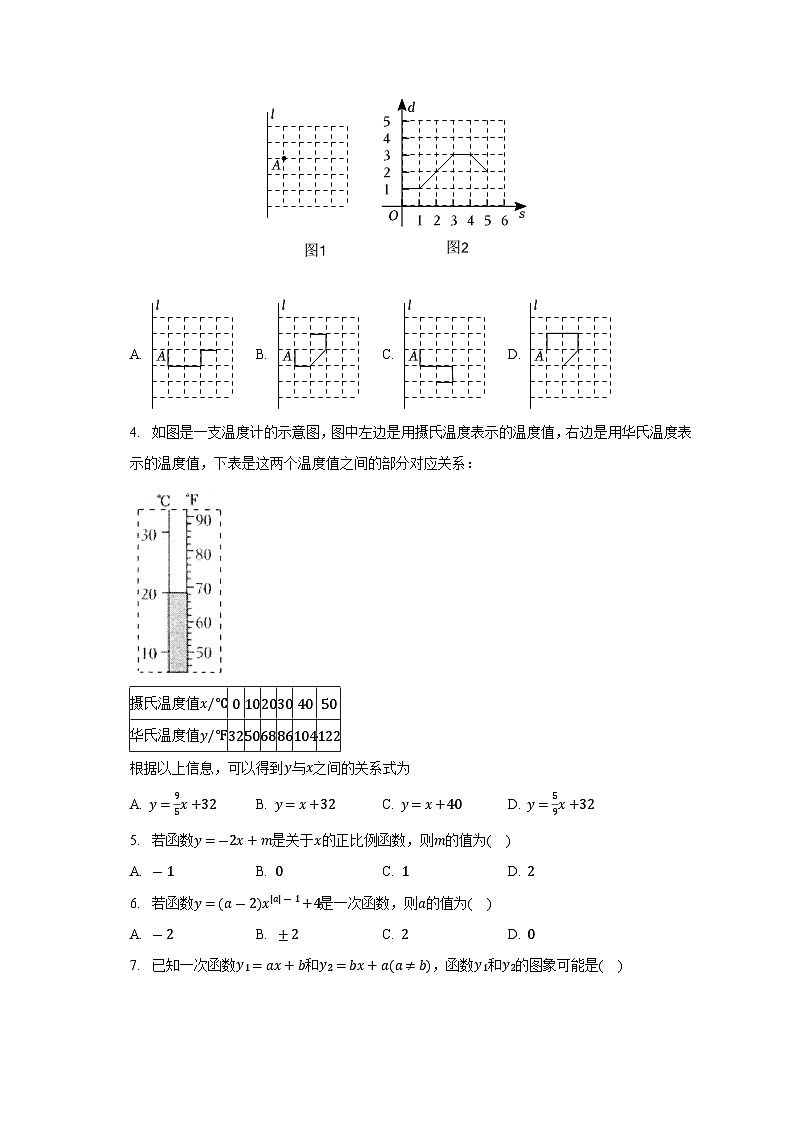
D. 当时，混合液的温度保持不变3.  如图，动点从点出发，在边长为的小正方形组成的网格平面内运动设点经过的路程为，点到直线的距离为，已知与的关系如图所示则下列选项中，可能是点的运动路线的是(    )
A.  B.  C.  D. 4.  如图是一支温度计的示意图，图中左边是用摄氏温度表示的温度值，右边是用华氏温度表示的温度值，下表是这两个温度值之间的部分对应关系：
 摄氏温度值华氏温度值根据以上信息，可以得到与之间的关系式为A.  B.  C.  D. 5.  若函数是关于的正比例函数，则的值为(    )A.  B.  C.  D. 6.  若函数是一次函数，则的值为(    )A.  B.  C.  D. 7.  已知一次函数和，函数和的图象可能是(    )A.  B.
C.  D. 8.  如果关于的一次函数的图象不经过第二象限，且关于的分式方程有整数解，那么整数的值不可能是(    )A.  B.  C.  D. 9.  如图，在平面直角坐标系中，点，，直线交坐标轴于点，，且，点在直线上，且，则直线的函数表达式为(    )
 A.  B.  C.  D. 10.  甲、乙两个工程队完成某项工程，首先甲队单独做了天，然后乙队加入合作，完成剩下的全部工程设工程总量为单位，工程进度满足下图所示的函数关系，那么实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少(    )
 A. 天 B. 天 C. 天 D. 天11.  如图，一次函数与的图象交于点，则关于、的方程组的解是(    )
A.  B.  C.  D. 12.  甲、乙两车同时从地出发，以各自的速度匀速向地行驶，甲车到达地后停止行驶，乙车到达地后，停留分钟，然后按原路以另一速度匀速返回地，已知两车分别距地的路程千米与行驶时间小时之间的函数图象如图所示，则下列说法错误的是(    )
 A. 甲车的速度是
B. 乙车返回地时的速度为
C. 甲车与乙车的相遇时间为小时
D. 甲车到达地时，乙车与地之间的距离为第II卷（非选择题）二、填空题（本大题共4小题，共12.0分）13.  在球的表面积公式中，常量是______ ．14.  已知直线经过点，则的立方根为          ．15.  如图，在平面直角坐标系中，直线分别交轴、轴于，两点，点在的内部不包含边界，则的取值范围是          ．
 16.  元朝朱世杰的算学启蒙一书记载：“今有良马日行二百四十里，驽马日行一百五十里．驽马先行一十二日，问良马几何日追及之．”如图是两匹马行走路程关于行走时间的函数图象，则两图象交点的坐标是______．三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）17.  本小题分
将长为，宽为的长方形白纸按下图所示的方法黏合起来，黏合部分的宽为．
 求张白纸黏合后的长度设张白纸黏合后的总长度为，写出与之间的关系式，并求时的值及时的值设张白纸黏合后的总面积为 ，写出与之间的关系式，并求时的值及时的值．18.  本小题分
某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量升与时间分钟之间的关系如折线图所示，根据图象解答下列问题：
在这个变化过程中，自变量、因变量是什么？
洗衣机的进水时间是多少分钟？清洗时洗衣机的水量是多少升？
时间为分钟时，洗衣机处于哪个过程？
19.  本小题分
如图所示，在三角形中，是三角形的高，且，点是上的一个动点，由点向点运动，其速度与时间的变化关系如图所示．
由图知，点运动的时间为______，速度为______，点停止运动时距离点 ______；
求在点的运动过程中，三角形的面积与运动时间之间的关系式；
当点停止运动后，求三角形的面积．

 20.  本小题分
如图，，两地相距千米，甲、乙两人于某日下午从地前往地，图中的折线和线段分别表示甲与乙所行驶的路程和时间的关系根据图象回答下列问题：
图中因变量是______ ；
甲出发______ 小时后，乙才开始出发；
甲在段路程中的平均速度是______ 千米小时；乙的平均速度是______ 千米小时；
根据图象上的数据，乙出发后经过______ 小时就追上甲．
21.  本小题分
自变量的函数值我们通常记作，表示自变量时，函数的函数值，已知函数，其中为常数．
若，求的值；
若存在唯一一个自变量的值，使得另一个函数，，试求满足条件的的值；
若存在实数且，使得，试求实数的取值范围．22.  本小题分
已知与成正比例，且时，．求关于的函数表达式．当时，求的值．23.  本小题分
在平面直角坐标系中，有，两点，另有一次函数的图象．若，，判断函数的图象与线段是否有交点请说明理由．当时，函数的图象与线段有交点，求的取值范围．若，求证：函数的图象一定经过线段的中点．24.  本小题分
在平面直角坐标系内有三点、、．
求过其中两点的直线的函数表达式选一种情形作答；
判断、、三点是否在同一直线上，并说明理由．25.  本小题分
李师傅将容量为升的货车油箱加满后，从工厂出发运送一批物资到某地行驶过程中，货车离目的地的路程千米与行驶时间小时的关系如图所示中途休息、加油的时间不计当油箱中剩余油量为升时，货车会自动显示加油提醒设货车平均耗油量为升千米，请根据图象解答下列问题：
直接写出工厂离目的地的路程；
求关于的函数表达式；
当货车显示加油提醒后，问行驶时间在怎样的范围内货车应进站加油？

答案和解析 1.【答案】 【解析】解：选项中，长方形的长面积宽，其中宽是定值，故是函数关系；
选项中，正方形的面积，故是函数关系；
选项中，等腰三角形的面积底高，高的值是不确定的，故不是函数关系；
选项中，圆的周长半径，故是函数关系．2.【答案】 【解析】解：根据图象可知：在这个变化过程中，自变量是时间，因变量是混合液的温度，
项的说法正确，
故A项不符合题意；
根据图象可知：混合液的温度小时之间随着时间的增大而下降，在小时之间随着时间的增大混合液的温度保持不变，在小时之间随着时间的增大混合液的温度减小，
项的说法不正确，
故B项符合题意；
根据图象可知：当时间为时，混合液的温度为，
项的说法正确，
项不符合题意；
根据图象可知：当时，混合液的温度保持不变，
项的说法正确，
故D项不符合题意；
故选：．
观察函数图象，通过函数图象中的信息对每一项判断即可解答．
本题考查了从函数图象中获取信息，读懂函数图象是解题的关键．3.【答案】 【解析】解：由图得：当点经过的路程为时，点到直线的距离不变，故点应先沿平行于的线运动，
当点经过的路程为时，点到直线的距离增加到，
当点经过的路程为时，点到直线的距离不变，故点应沿平行于的线运动，
当点经过的路程为时，点到直线的距离变为，故点往方向运动，
故选：．
分别分析当点经过的路程为时、时、时、时的点到直线的距离变化情况即可解答此题．
本题考查了动点问题的函数图象的应用，结合图形分析题意并解答是解题关键．4.【答案】 【解析】【分析】根据题意摄氏温度与华氏温度之间存在的函数关系，则设与之间的函数关系式为，然后把和代入得到关于、的方程，解方程组即可；
此题考查了根据实际问题列出函数关系式．【解答】解：设与之间的函数关系式为，
将和代入得，，，
解得，，
与之间的函数关系式为 ．5.【答案】 【解析】解：函数是正比例函数，
，
故选：．
根据正比例函数的定义，求出的值即可．
本题考查的是正比例函数的定义，一般地形如是常数，的函数叫做正比例函数．6.【答案】 【解析】解：是关于的一次函数，
且，
且，
且，
．
故选：．
根据一次函数的定义可知，、为常数，，自变量的次数为，即可求解．
本题考查了一次函数的定义，熟练掌握一次函数的定义和性质是解题的关键．7.【答案】 【解析】解：由图象可知：
当时，，
分情况讨论：
当、时，直线和直线都经过一、二、三象限，只有选项A符合；
当、时，直线经过一、二、四象限，直线经过一、三、四象限，没有符合的选项；
当、时，直线经过一、三、四象限，直线经过一、二、四象限，没有符合的选项；
当、时，直线和直线都经过二、三、四象限，没有符合的选项．
故选：．
分、，、，、，、四种情况讨论，判断出直线经过的象限，找出符合题意的选项，即可做出判断．
本题主要考查的是一次函数图象与系数的关系，分类讨论思想，掌握一次函数的图象和性质是解题的关键．8.【答案】 【解析】略9.【答案】 【解析】略10.【答案】 【解析】甲队的工作效率是，甲队完成总工程需要天．甲、乙两个工程队合作的工作效率是--，实际完成这项工程所用的时间是天，天．11.【答案】 【解析】解：一次函数与的图象交于点，
关于、的方程组的解是．
故选：．
根据函数与方程组的关系结合交点坐标即可求得方程组的解．
本题主要考查了一次函数图象与二元一次方程组的关系，函数图象交点坐标为两函数解析式组成的方程组的解．12.【答案】 【解析】解：由图象可得，甲车的速度是，
故选项A正确，不符合题意；
乙车返回地时的速度为，
故选项B正确，不符合题意；
设行驶过程中，乙车与甲车的相遇时间为小时，
则，
解得，
故选项C正确，不符合题意；
甲车到达地时用的时间为小时，
所以甲车到达地时，乙车与地之间的距离为千米，
故选项D错误，符合题意．
故选：．
根据图象结合速度、路程、时间之间的关系，可以逐项判断．
本题主要考查了一次函数的综合题，解答要注意数形结合思想的运用．13.【答案】 【解析】解：在球的表面积公式中，是常量，、是变量，
故答案为：．
根据常量、变量的定义，可得答案．
本题考查了常量与变量，常量是在事物的变化中保持不变的量．14.【答案】 【解析】略15.【答案】 【解析】略16.【答案】 【解析】【分析】
本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．
根据题意可以得到关于的方程，从而可以求得点的坐标，本题得以解决．
【解答】
解：令，
解得，，
则，
点的坐标为，
故答案为：．17.【答案】解：．为正整数，
当时，
当时，．为正整数，
当时，
当时，． 【解析】本题考查的是函数关系式及探索图形变化的规律性知识，结合图形理清数量之间关系是解决此题关键．
根据白纸长度减去张重合部分的长度即可；
根据纸条总长度纸条的张数纸条张数，把相关数值代入即可求解；
同，利用长方形面积公式即可得到与的关系式，再把数值代入求解即可．18.【答案】解：自变量是时间，因变量是水量；
洗衣机的进水时间是分钟，清洗时洗衣机中的水量升；
由于排水速度与进水速度相同，排水量和进水量相同，所以排水时间与进水时间相同，即排水时间为分钟，
所以洗衣机清洗衣服所用的时间：分钟；
答：故可得时间分钟时，洗衣机处于清洗过程． 【解析】根据函数图象可判断，这是水量与时间之间的关系；
结合函数图象可得进水时间是分钟，清洗时洗衣机的水量是升；
分钟是进水过程，分钟是清洗过程，分钟过后是排水过程．
本题考查了函数的图象，要求结合实际情况理解图象各个点的实际意义．19.【答案】解：，，
根据题意得，
即；
当时，，
故的面积为． 【解析】解：解：根据题意和图象，可得点运动的时间为，速度为．
当点停止运动时，，此时距离点：，
故答案为：，，；
见答案；
见答案；
根据图象解答即可；
根据三角形的面积公式，可得答案；
根据三角形的面积公式，可得答案．
本题主要考查了动点问题的函数图象，涉及求函数解析式，求函数值问题，能读懂函数图象是解决问题的关键．20.【答案】时间         【解析】解：由图象可知，图中自变量是时间；
故答案为：时间；
由图象可知，甲在小时，开始出发，乙在小时，开始出发，
，
甲出发小时后，乙才开始出发，
故答案为：；
，，
甲在段路程中的平均速度是千米小时；乙的平均速度是千米小时，
故答案为：；；
设乙出发后经过小时就追上甲，
依题意得，，
解得，
乙出发后经过小时就追上甲，
故答案为：．
根据坐标系中轴表示的量是自变量，轴表示的量是因变量进行作答即可；
观察图象即可；
根据甲在段小时的路程为千米，乙小时的路程为千米，进行计算求解即可；
设乙出发后经过小时就追上甲，依题意得，，计算求解即可．
本题考查了函数图象，一元一次方程的应用．从图象中获取正确的信息是解题的关键．21.【答案】解：当时，，
；
由题意得，则，
存在唯一一个自变量的值，使得另一个函数，
，
解得或；
的对称轴为，
，
，
，
，
，
． 【解析】将，代入函数解析式即可求解；
由题意得，即，则，解得或；
由函数的对称性可知，得到，结合的范围即可求的范围．
本题考查二次函数的综合应用；熟练掌握二次函数的性质，能将所求问题转化为二次函数的最值问题是解题的关键．22.【答案】【小题】【小题】 【解析】 略
 略23.【答案】【小题】由题意，线段的表达式为，当，时，一次函数表达式为，将代入，得，此时该函数图象与线段无交点．【小题】将代入，得一次函数表达式为，将代入，得，，解得．【小题】证明：将代入，得一次函数表达式为，由题意可得，线段的中点为，当时，，在一次函数的图象上，若，一次函数的图象一定经过线段的中点． 【解析】 见答案
 见答案
 见答案24.【答案】解：设、两点所在直线解析式为，
，
解得，
直线的解析式．
当时，，
点不在直线上，即点、、三点不在同一条直线上． 【解析】根据、两点的坐标求得直线的解析式．
把的坐标代入看是否符合解析式即可判定．
本题考查了待定系数法求解析式，以及判定是否是直线上的点，掌握一次函数图像上的点的坐标特征是关键．25.【答案】解：由图象，得时，，
工厂离目的地的路程为千米，
答：工厂离目的地的路程为千米；
设，
将和代入得，
，
解得：，
关于的函数表达式：，
答：关于的函数表达式：；
当油箱中剩余油量为升时，
千米，
，
解得：小时，
当油箱中剩余油量为升时，
千米，
，解得：小时，
，
随的增大而减小，
的取值范围是． 【解析】由图象直接求出工厂离目的地的路程；
用待定系数法求出函数解析式即可；
当油箱中剩余油量为升时和当油箱中剩余油量为升时，求出的取值即可．
本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．