2024泰安肥城高三上学期9月阶段测试数学含答案

这是一份2024泰安肥城高三上学期9月阶段测试数学含答案，文件包含山东省泰安肥城市2023-2024学年高三9月阶段测试数学试题docx、高三数学答案docx等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。
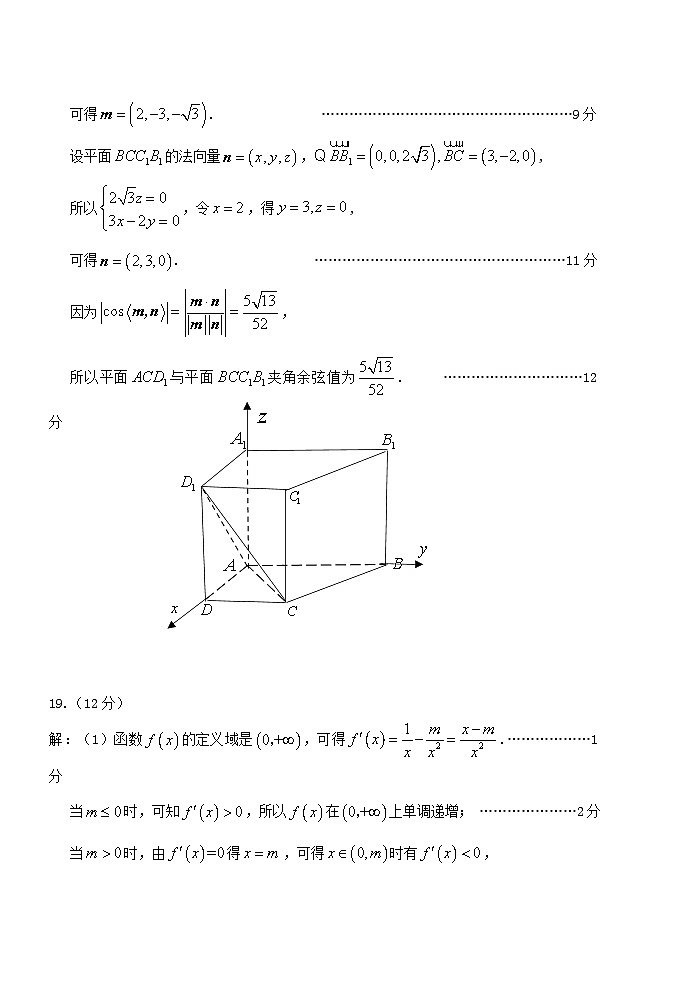
高三数学参考答案及评分意见一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的．题号12345678答案CBDCADAB二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.题号9101112答案ACDACABDABD三、填空题：本题共4小题，每小题5分，共20分.13.      14.        15.        16. 四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.（10分）解：（1）在中，由余弦定理得，所以. …………………………………3分由正弦定理，得 . ……………5分（2）因为,所以，  由,得 .           …………………………………………7分在中，，得,  …………………………8分因为,所以.……………………………………………………10分18.（12分）解：（1）证明：在四棱锥中，，,,.      ……………………………………2分,.                     ……………………………………… 3分又,.   ……………………………………5分（2）,可得两两垂直，  以所在直线分别为轴，轴，轴，建立空间直角坐标系.与平面所成角为,..又，. …………………7分设平面的法向量，,,所以，令，得,可得.               ………………………………………………9分   设平面的法向量，,所以，令，得,可得.                   ………………………………………………11分   因为，所以平面与平面夹角余弦值为.     …………………………12分            19.（12分）解：（1）函数的定义域是，可得.………………1分当时，可知，所以在上单调递增； …………………2分当时，由得，可得时有，时有，所以在上单调递减，在上单调递增.  …………………………………………………………4分综上可得，当时，在上单调递增；当时，在上单调递减，在上单调递增. ………………5分 （2）证明：当时，要证成立，只需证成立，只需证即可.  ………………………………………………………6分因为，由（1）知，. 令，  ……………………………………8分由，可得时有，时有，所以在上单调递减，在上单调递增，可知，有.    ………………………………………11分所以有，从而当时，成立. ………………12分 20.（12分）解：（1）由题意得：，所以，即.………………………………………2分又，所以，所以数列是以1为首项，为公差的等差数列，所以，即，    …………………………………………………3分所以，两式相减得，即，所以，        …………………………………………………5分因此的通项公式为.          …………………………………………………6分（2）由（1）可得：，.…………7分因为，             …………………………………………………10分所以.…………………………………………………12分21.（12分）解：（1）由题意可知，的可能取值为，        ………………………………1分所以由概率乘法公式得：，，.所以的分布列为： ……………………………………3分 （2）由全概率公式可知：                …………………………………4分，所以，即.………………………5分所以. ……………………………………………………………6分又，所以数列是以为首项，以为公比的等比数列，所以，即.……………7分（3）由全概率公式得：，所以.  …………………………………………………………………8分又，所以，所以.  …………………………9分又，所以，         ………………………………10分所以，，………………………………11分所以. …………………………12分22.（12分）解：（1）设点坐标为，则由题意得：，……………2分整理得：.即的方程为.  …………………………………………………………………3分（2）如图，不妨设三个顶点中有两个在轴右侧（包括轴）， 且设、、三点的坐标分别为、、，的斜率为，则有，.  ………………………………………4分又、、三点在抛物线上，所以，，，代人上面两式得：，.  ………………………………………5分由于，即，所以，，…………………7分所以，，所以，，且有.     ………………………………………9分所以正方形边长为. ………………………………………11分当且仅当时， 即点为原点时等号成立.