2014年广州市中考数学试卷

2014年广东省广州市中考数学试卷

一、选择题（本大题共10小题，每小题3分，满分30分）

1．（）的相反数是（    ）

（A）            （B）             （C）            （D）

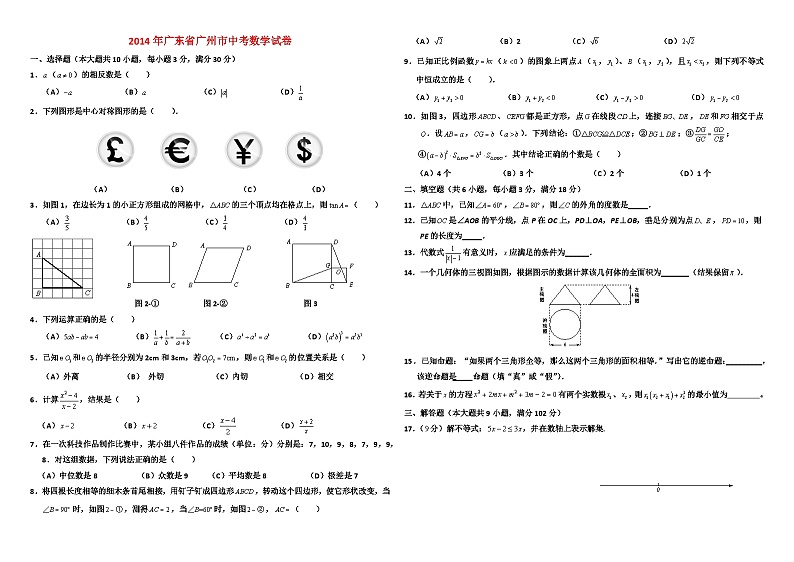
2．下列图形是中心对称图形的是（    ）．

（A）              （B）             （C）            （D）            

3．如图1，在边长为1的小正方形组成的网格中，的三个顶点均在格点上，则（    ）

（A）             （B）             （C）             （D）

图2-①           图2-②                   图3                            

4．下列运算正确的是（    ）

（A）    　　（B）      （C）    　　（D）

5．已知和的半径分别为2cm和3cm，若，则和的位置关系是（    ）

（A）外离           （B） 外切            （C）内切       　　 （D）相交

6．计算，结果是（    ）

（A）        　 （B）      　  （C）    　    （D）

7．在一次科技作品制作比赛中，某小组八件作品的成绩（单位：分）分别是：7，10，9，8，7，9，9，8．对这组数据，下列说法正确的是（    ）

（A）中位数是8     　　 （B）众数是9     （C）平均数是8     　   （D）极差是7   

8．将四根长度相等的细木条首尾相接，用钉子钉成四边形，转动这个四边形，使它形状改变，当时，如图，测得，当时，如图，（    ）

（A）       　    （B）2     　     （C）         　    （D）

9．已知正比例函数（）的图象上两点（，）、（，），且，则下列不等式 中恒成立的是（    ）．

（A）     　　 （B）         （C）  　　　　 （D）

10．如图3，四边形、都是正方形，点在线段上，连接，和相交于点．设，（）．下列结论：①；②；③；

④．其中结论正确的个数是（    ）

（A）4个            （B）3个              （C）2个             （D）1个

二、填空题（共6小题，每小题3分，满分18分）

11．中，已知，，则的外角的度数是_____．

12．已知是∠AOB的平分线，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为点，，则PE的长度为_____．

13．代数式有意义时，应满足的条件为______．

14．一个几何体的三视图如图，根据图示的数据计算该几何体的全面积为_______（结果保留）．

15．已知命题：“如果两个三角形全等，那么这两个三角形的面积相等．”写出它的逆命题：_________，该逆命题是_____命题（填“真”或“假”）．

16．若关于的方程有两个实数根、，则的最小值为　　　　。

三、解答题（本大题共9小题，满分102分）

17．（分）解不等式：，并在数轴上表示解集.

18．（分）如图5，平行四边形的对角线相交于点，过点且与、分别交于点，求证：．

19．（10分）已知多项式.

（1）化简多项式；

（2）若，求的值.

20．（10分）某校初三（1）班50名学生需要参加体育“五选一”自选项目测试，班上学生所报自选项目的情况统计表如下：

（1）求，的值；

（2）若将各自选项目的人数所占比例绘制成扇形统计图，求“一分钟跳绳”对应扇形的圆心角的度数；

（3）在选报“推铅球”的学生中，有3名男生，2名女生，为了了解学生的训练效果，从这5名学生中随机抽取两名学生进行推铅球测试，求所抽取的两名学生中至多有一名女生的概率．

21．（12分）已知一次函数的图像与反比例函数的图像交于两点，点的横坐标为2．（1）求的值和点的坐标；（2）判断点的象限，并说明理由．

22、（12分）从广州某市，可乘坐普通列车或高铁，已知高铁的行驶路程是400千米，普通列车的行驶路程是高铁的行驶路程的1.3倍．

（1）求普通列车的行驶路程；

（2）若高铁的平均速度（千米/时）是普通列车平均速度（千米/时）的2.5倍，且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时，求高铁的平均速度．

23、（12分） 如图6，中，，．

（1）动手操作：利用尺规作以为直径的，并标出与的交点，与的交点（保留作图痕迹，不写作法）：

（2）综合应用：在你所作的圆中：

①求证：；

②求点到的距离．

24．（14分）已知平面直角坐标系中两定点A（-1，0），B（4，0），抛物线（）过点A、B，顶点为C．点P（m，n）（n<0）为抛物线上一点．

（1）求抛物线的解析式与顶点C的坐标．

（2）当∠APB为钝角时，求m的取值范围．

（3）若，当∠APB为直角时，将该抛物线向左或向右平移t（）个单位，点P、C移动后对应的点分别记为、，是否存在t，使得首尾依次连接A、B、、所构成的多边形的周长最短？若存在，求t值并说明抛物线平移的方向；若不存在，请说明理由．

25．（14）如图7，梯形中，，，,，，点为线段上一动点（不与点 重合），关于的轴对称图形为，连接，设，的面积为，的面积为．

（1）当点落在梯形的中位线上时，求的值；

（2）试用表示，并写出的取值范围；

（3）当的外接圆与相切时，求的值．

广州市2014年初中毕业生学业考试数  学

一、1． A 2． D3． D 4．  C  5． A 6． B 7． B 8． A 9． C 10． B 

二、11．12． 10    13． 14． 15．如果两个三角形的面积相等，那么这两个三角形全等．假命题．16．

17．解：移项得，，合并同类项得，，

系数化为1得，，在数轴上表示为：

18．证明：∵平行四边形的对角线相交于点

∴，，∴

在和中，，∴

19．解:（1）

（2）,则

20．解：（1）          

（2）“一分钟跳绳”所占圆心角=

（3）至多有一名女生包括两种情况有1个或者0个女生，列表图：

有1个女生的情况：12种          有0个女生的情况：6种

至多有一名女生包括两种情况18种

至多有一名女生包括两种情况===0.90

21．解：（1）将与联立得，

点是两个函数图像交点，将带入式得解得

故一次函数解析式为，反比例函数解析式为

将代入得，，的坐标为

（2）点在第四象限，理由如下：

一次函数经过第一、三、四象限，反比例函数经过第二、四象限，

因此它们的交点都是在第四象限.

22、解：（1）依题意可得，普通列车的行驶路程为400×1.3=520（千米）

（2）设普通列车的平均速度为千米/时，则高铁平均速度为千米/时．

依题意有：，可得： 答：高铁平均速度为 2.5×120=300千米/时．

23、 解：（1）如图所示，圆为所求

（2）①如图连接，设,

又

则

，

②连接,过作于,过作于

cosC=, 又， ,

又为直径，

设，则，在和中，

有，即，解得：

即

又，即，

24．解：（1）依题意把的坐标代入得 ，解得

抛物线解析式为

顶点横坐标,将代入抛物线得 

（2）如图,当时,设,

则

过作直线轴, ，

，(注意用整体代入法)

解得，,

当在之间时，或时，为钝角.

（3）依题意，且，

设移动（向右，向左），

连接，则

又的长度不变，四边形周长最小，只需最小即可

将沿轴向右平移5各单位到处，沿轴对称为

∴当且仅当、B、三点共线时，最小，且最小为，此时

，设过的直线为，代入

∴  即

将代入，得：，解得：

∴当，P、C向左移动单位时，此时四边形ABP’C’周长最小。

25．解：（1）如图，为梯形的中位线，则，过点作于点，则有：

，在中，有，

在中，，

又，，解得：

（2）如图，交于点，与关于对称，

则有：，

又

，，

又与关于对称，

（3）如图，当的外接圆与相切时，则为切点.

的圆心落在的中点，设为

则有，过点作，

连接，得

           则

又

解得：（舍去）

①                          ②                          ③