

2009年潍坊市中考数学试卷
展开2009年潍坊市中考数学试题
一、选择题(12小题,每小题3分)
1.下列运算正确的是( )
A. B. C. D.
2.一个自然数的算术平方根为,则和这个自然数相邻的下一个自然数是( )
A. B. C. D.
3.太阳内部高温核聚变反应释放的辐射能功率为千瓦,到达地球的仅占20亿分之一,到达地球的辅射能功率为( )千瓦.(用科学计数法表示,保留2个有效数字)
A. B. C. D.
4.已知关于的一元二次方程的两个实数根是,且,则的值是( )
A.8 B. C.6 D.5
5.某班50名同学分别站在公路的A、B两点处,A、B两点相距1000米,A处有30人,B处有20人,要让两处的同学走到一起,并且使所有同学走的路程总和最小,那么集合地点应选在( )
A.A点处 B.线段的中点处C.线段上,距A点米处D.线段上,距A点400米处
6.关于的方程有实数根,则整数的最大值是( )
A.6 B.7 C.8 D.9
7.甲、乙两盒中分别放入编号为1、2、3、4的形状相同的4个小球,从甲盒中任意摸出一球,再从乙盒中任意摸出一球,将两球编号数相加得到一个数,则得到数( )的概率最大.
A.3 B.4 C.5 D.6
8.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得,在C点测得,又测得米,则小岛B到公路l的距离为( )米.
A.25 B. C. D.
9.已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连结AC,若,则BD的长为( )
A. B. C. D.
10.如图,已知中,,将绕顶点C顺时针旋转至的位置,且三点在同一条直线上,则点A经过的最短路线的长度是( )cm.
A.8 B. C. D.
11.如图,在中,,分别以为圆心,以的长为半径作圆,将截去两个扇形,则剩余(阴影)部分的面积为( )cm2.
A. B. C. D.
12.在同一平面直角坐标系中,反比例函数与一次函数交于两点,O为坐标原点,则的面积为( )
A.2 B.6 C.10 D.8
二、填空题(本题共5小题,共15分.只要求填写最后结果,每小题填对得3分.)
13.分解因式: .
14.方程的解是 .
15.在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O逆时针旋转90°后的.
16.如图,正方形的边长为10,点E在CB的延长线上,,点P在边CD上运动(C、D两点除外),EP与AB相交于点F,若,四边形的面积为,则关于的函数关系式是 .
17.已知边长为的正三角形,两顶点分别在平面直角坐标系的轴、轴的正半轴上滑动,点C在第一象限,连结OC,则OC的长的最大值是 .
三、解答题(本题共7小题,共69分)
18.(8分)某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱个,请分别写出从纸箱厂购买纸箱的费用(元)和蔬菜加工厂自己加工制作纸箱的费用(元)关于(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
19.(9分)新星公司到某大学从应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
(1)写出4位应聘者的总分;
(2)就表中专业知识、英语水平、参加社会实践与社团活动等三项的得分,分别求出三项中4人所得分数的方差;
(3)由(1)和(2),你对应聘者有何建议?
项目
应聘者 | 专业知识 | 英语水平 | 参加社会实践与社团活动等 |
A | 85 | 85 | 90 |
B | 85 | 85 | 70 |
C | 80 | 90 | 70 |
D | 90 | 90 | 50 |
20.(9分)已知,延长BC到D,使.取的中点,连结交于点.
(1)求的值;(2)若,求的长.
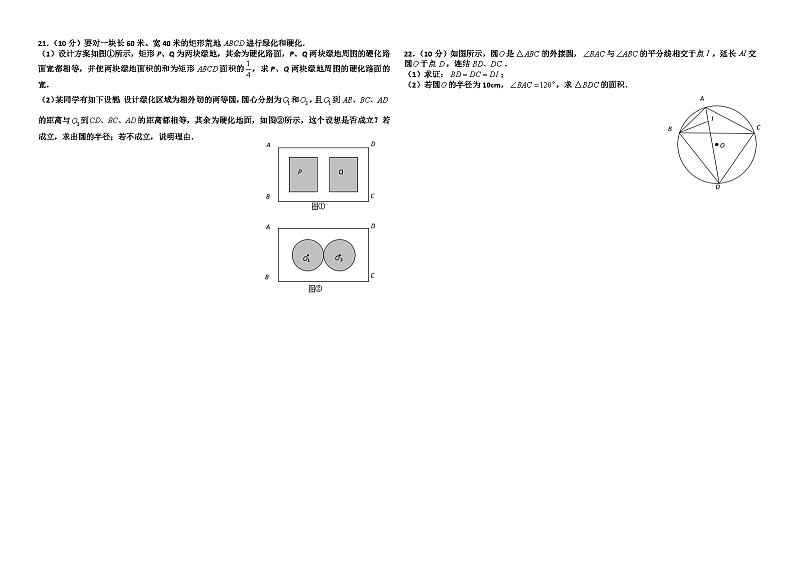
21.(10分)要对一块长60米、宽40米的矩形荒地进行绿化和硬化.
(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形面积的,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为和,且到的距离与到的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
22.(10分)如图所示,圆是的外接圆,与的平分线相交于点,延长交圆于点,连结.
(1)求证:;
(2)若圆的半径为10cm,,求的面积.
23.(11分)在四边形中,,且.取的中点,连结.
(1)试判断三角形的形状;
(2)在线段上,是否存在点,使.若存在,请求出的长;若不存在,请说明理由.
24.(12分)如图,在平面直角坐标系中,半径为1的圆的圆心在坐标原点,且与两坐标轴分别交于四点.抛物线与轴交于点,与直线交于点,且分别与圆相切于点和点.
(1)求抛物线的解析式;
(2)抛物线的对称轴交轴于点,连结,并延长交圆于,求的长.
(3)过点作圆的切线交的延长线于点,判断点是否在抛物线上,说明理由.
2009年潍坊市中考数学试题答案
一、
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | D | B | A | D | A | C | C | B | C | D | A | B |
二、
13. 14. 15.见右图
16. 17.
三、18.(8分)
解:(1)从纸箱厂定制购买纸箱费用:
····································································2分
蔬菜加工厂自己加工纸箱费用:
.···································································4分
(2),
由,得:,
解得:.·····························································5分
当时,,
选择方案一,从纸箱厂定制购买纸箱所需的费用低.····························6分
当时,,
选择方案二,蔬菜加工厂自己加工纸箱所需的费用低.··························7分
当时,,
两种方案都可以,两种方案所需的费用相同.·································8分
19.(9分)解:(1)应聘者A总分为86分;应聘者B总分为82分;应聘者C总分为81分;应聘者D总分为82分. 4分
(2)4位应聘者的专业知识测试的平均分数,
方差为:·····························································5分
4位应聘者的英语水平测试的平均分数,
方差为:.····························································6分
4位应聘者参加社会实践与社团活动等的平均分数为,
方差为:.····························································7分
(3)对于应聘者的专业知识、英语水平的差距不大,但参加社会实践与社团活动等方面的差距较大,影响学生的最后成绩,将影响学生就业.学生不仅注重自己的文化知识的学习,更应注重社会实践与社团活动的开展,从而促进学生综合素质的提升. 9分
20.(9分)解:(1)过点F作,交于点.
为的中点为的中点,.···················································2分
由,得,
·······································4分
····································································6分
(2) 又
.···································································9分
21.(10分)解:(1)设两块绿地周围的硬化路面的宽都为米,根据题意,得:
····································································3分
解之,得:····························································5分
经检验,不符合题意,舍去.所以,两块绿地周围的硬化路面宽都为10米.···········6分
(2)设想成立.·······················································7分
设圆的半径为米,到的距离为米,根据题意,得:
····································································9分
解得:.符合实际.所以,设想成立,此时,圆的半径是10米.···················10分
22.(10分)(1)证明:平分
····································································2分
平分
,又
为等腰三角形
····································································5分
(2)解:当时,为钝角三角形,
圆心在外,
连结,
,
,为正三角形.························································8分
又知,
答:的面积为cm2.····················································10分
23.(11分)解:(1)在四边形中,,,
四边形为直角梯形(或矩形).
过点作,垂足为,,
又点是的中点,点是的中点,
又,
,···································································3分
与是全等的等腰直角三角形,
,
是等腰直角三角形.·····················································5分
(2)存在点使.·······················································6分
以为直径,为圆心作圆.
当时,四边形为矩形,,
圆与相切于点,此时,点与点重合,存在点,使得,
此时.·······························································7分
当时,四边形为直角梯形,
,,圆心到的距离小于圆的半径,圆与相交,上存在两点,使,····················8分
过点作,在中,,
连结,则,
在直角三角形中,,
.同理可得:.
综上所述,在线段上存在点,使.
当时,有一点,;当时,有两点,.········································11分
24.(12分)
解:(1)圆心在坐标原点,圆的半径为1,
点的坐标分别为
抛物线与直线交于点,且分别与圆相切于点和点,
.···································································2分
点在抛物线上,将的坐标代入
,得: 解之,得:
抛物线的解析式为:.···················································4分
(2)抛物线的对称轴为,
.·····································6分
连结,
,,
又,
,.·································································8分
(3)点在抛物线上.····················································9分
设过点的直线为:,将点的坐标代入,得:,
直线为:.···························································10分
过点作圆的切线与轴平行,点的纵坐标为,
将代入,得:.点的坐标为,·············································11分
当时,,所以,点在抛物线上.···········································12分
2018年潍坊市中考数学试卷: 这是一份2018年潍坊市中考数学试卷,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2017年潍坊市中考数学试卷: 这是一份2017年潍坊市中考数学试卷,共7页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
2016年潍坊市中考数学试卷: 这是一份2016年潍坊市中考数学试卷,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












