

2014年山东省济宁市中考数学试卷答案
展开2014年山东省济宁市中考数学试卷
一、选择题:本大题共10小题,每小题3分,共30分.
1.实数1,﹣1,﹣,0,四个数中,最小的数是( )
A.0 B.1 C.﹣1 D.﹣
2.化简﹣5ab+4ab的结果是( )
A.﹣1 B.a C.b D.﹣ab
3.把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是( )
A.两点确定一条直线 B. 垂线段最短
C.两点之间线段最短 D. 三角形两边之和大于第三边
4.函数y=中的自变量x的取值范围是( )
A.x≥0 B.x≠﹣1 C.x>0 D.x≥0且x≠﹣1
5.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为( )
A.10cm2 B.10πcm2 C.20cm2 D.20πcm2
6.从总体中抽取一部分数据作为样本去估计总体的某种属性.下面叙述正确的是( )
A. 样本容量越大,样本平均数就越大 B. 样本容量越大,样本的方差就越大
C. 样本容量越大,样本的极差就越大 D.样本容量越大,对总体的估计就越准确
7.如果ab>0,a+b<0,那么下面各式:①=,②•=1,③÷=﹣b,其中正确的是( )
A.①② B.②③ C.①③ D.①②③
8.“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( )
A.m<a<b<n B.a<m<n<b C.a<m<b<n D. m<a<n<b
9.如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为( )
A.(﹣a,﹣b) B.(﹣a,﹣b﹣1) C.(﹣a,﹣b+1) D. (﹣a,﹣b+2)
10.如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )
A.10cm. B.24cm C.26cm D.52cm
二、填空题:本大题共5小题,每小题3分,共15分.
11.如果从一卷粗细均匀的电线上截取1米长的电线,称得它的质量为a克,再称得剩余电线的质量为b克,那么原来这卷电线的总长度是 米.
12.如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB的长为 .
13.若一元二次方程ax2=b(ab>0)的两个根分别是m+1与2m﹣4,则= .
14.如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
15.如图(1),有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△DEO的重心;固定点O,将△ODE顺时针旋转,使得OD经过点C,如图(2),则图(2)中四边形OGCF与△OCH面积的比为 .
三、解答题:本大题共7小题,共55分.
16.(6分)已知x+y=xy,求代数式 + ﹣(1﹣x)(1﹣y)的值.
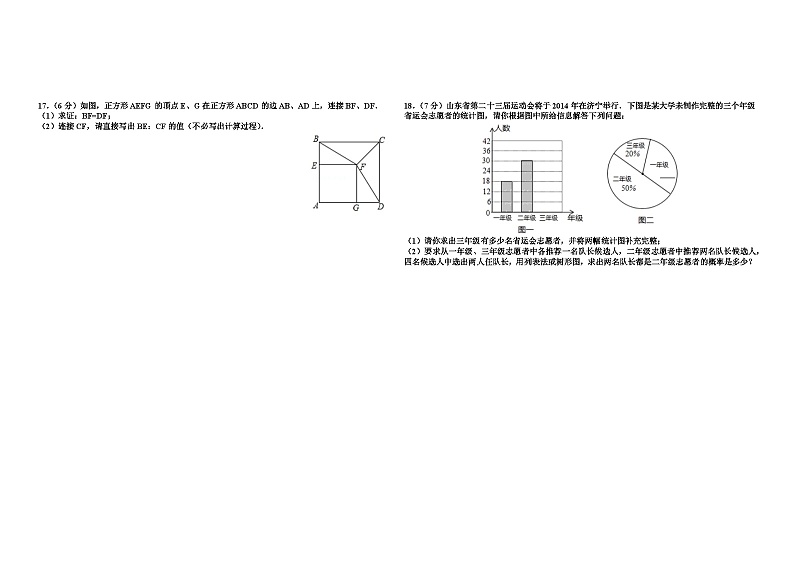
17.(6分)如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
(1)求证:BF=DF;
(2)连接CF,请直接写出BE:CF的值(不必写出计算过程).
18.(7分)山东省第二十三届运动会将于2014年在济宁举行.下图是某大学未制作完整的三个年级省运会志愿者的统计图,请你根据图中所给信息解答下列问题:
(1)请你求出三年级有多少名省运会志愿者,并将两幅统计图补充完整;
(2)要求从一年级、三年级志愿者中各推荐一名队长候选人,二年级志愿者中推荐两名队长候选人,四名候选人中选出两人任队长,用列表法或树形图,求出两名队长都是二年级志愿者的概率是多少?
19.(8分)济宁市“五城同创”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了x天完成,乙做另一部分用了y天完成,其中x、y均为正整数,且x<46,y<52,求甲、乙两队各做了多少天?
20.(8分)在数学活动课上,王老师发给每位同学一张半径为6个单位长度的圆形纸板,要求同学们:
(1)从带刻度的三角板、量角器和圆规三种作图工具中任意选取作图工具,把圆形纸板分成面积相等的四部分;
(2)设计的整个图案是某种对称图形.
王老师给出了方案一,请你用所学的知识再设计两种方案,并完成下面的设计报告.
名 称 | 四等分圆的面积 | ||
方 案 | 方案一 | 方案二 | 方案三 |
选用的工具 | 带刻度的三角板 |
|
|
画出示意图 | |||
简述设计方案 | 作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份. |
|
|
指出对称性 | 既是轴对称图形又是中心对称图形 |
|
|
21.(9分)阅读材料:
已知,如图(1),在面积为S的△ABC中,BC=a,AC=b,AB=c,内切圆O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB=BC•r+AC•r+AB•r=(a+b+c)r.
∴r=.
(1)类比推理:若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r;
(2)理解应用:如图(3),在等腰梯形ABCD中,AB∥DC,AB=21,CD=11,AD=13,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,设它们的半径分别为r1和r2,求的值.
22.(11分)如图,抛物线y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
2014年山东省济宁市中考数学试卷答案
1. C.2. D.3. C.4. A.5. B.6. D.7. B.8.A.9. D.10. B.
11.(+1)米.12. 3+.13. 4.14. 2.15.4:3.
16.解:∵x+y=xy,
∴+﹣(1﹣x)(1﹣y)
=﹣(1﹣x﹣y+xy)
=﹣1+x+y﹣xy
=1﹣1+0
=0
17.(1)证明:∵四边形ABCD和AEFG都是正方形,
∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°,
∴BE=AB﹣AE,DG=AD﹣AG,∴BE=DG,
在△BEF和△DGF中,
∴△BEF≌△DGF(SAS),
∴BF=DF;
(2)解:∵BF=DF
∴点F在对角线AC上
∵AD∥EF∥BC
∴BE:CF=AE:AF=AE:AE=
∴BE:CF=.
18.解:(1)三个年级省运会志愿者的总人数=30÷50%=60(人),
所以三年级志愿者的人数=60×20%=12(人);
一年级志愿者的人数所占的百分比=1﹣50%﹣20%=30%;
如图所示:
(2)用A表示一年级队长候选人,B、C表示二年级队长候选人,D表示三年级队长候选人,画树形图为:,
共有12种等可能的结果,其中两人都是二年级志愿者的情况有两种,
所以P(两名队长都是二年级志愿者)==.
19.解:(1)设乙工程队单独完成这项工作需要x天,由题意得
+36()=1,解之得x=80,
经检验x=80是原方程的解.
答:乙工程队单独做需要80天完成;
(2)因为甲队做其中一部分用了x天,乙队做另一部分用了y天,
所以=1,即y=80﹣x,又x<46,y<52,
所以,解之得42<x<46,
因为x、y均为正整数,所以x=45,y=50,
答:甲队做了45天,乙队做了50天.
20.解:
名称 四等分圆的面积
方案 方案一 方案二 方案三
选用的工具 带刻度的三角板 带刻度三角板、量角器、圆规. 带刻度三角板、圆规. 画出示意图
简述设计方案 作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份. (1)以点O为圆心,以3个单位长度为半径作圆;
(2)在大⊙O上依次取三等分点A、B、C;
(3)连接OA、OB、OC.
则小圆O与三等份圆环把⊙O的面积四等分. (4)作⊙O的一条直径AB;
(5)分别以OA、OB的中点为圆心,以3个单位长度为半径作⊙O1、⊙O2;
则⊙O1、⊙O2和⊙O中剩余的两部分把⊙O的面积四等分.
指出对称性 既是轴对称图形又是中心对称图形. 轴对称图形 既是轴对称图形又是中心对称图形.
21.解:(1)如图2,连接OA、OB、OC、OD.
∵S=S△AOB+S△BOC+S△COD+S△AOD=+++=,
∴r=.
(2)如图3,过点D作DE⊥AB于E,
∵梯形ABCD为等腰梯形,
∴AE===5,
∴EB=AB﹣AE=21﹣5=16.
在Rt△AED中,
∵AD=13,AE=5,
∴DE=12,
∴DB==20.
∵S△ABD===126,
S△CDB===66,
∴===.
22.解:(1)∵y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,
∴,解得.
∴抛物线的解析式为y=x2﹣x﹣.
(2)如答图所示,过点A′作A′E⊥x轴于E,AA′与OC交于点D,
∵点C在直线y=2x上,∴C(5,10)
∵点A和A′关于直线y=2x对称,
∴OC⊥AA′,A′D=AD.
∵OA=5,AC=10,
∴OC===.
∵S△OAC=OC•AD=OA•AC,
∴AD=.
∴AA′=,
在Rt△A′EA和Rt△OAC中,
∵∠A′AE+∠A′AC=90°,∠ACD+∠A′AC=90°,
∴∠A′AE=∠ACD.
又∵∠A′EA=∠OAC=90°,
∴Rt△A′EA∽Rt△OAC.
∴,即.
∴A′E=4,AE=8.
∴OE=AE﹣OA=3.
∴点A′的坐标为(﹣3,4),
当x=﹣3时,y=×(﹣3)2+3﹣=4.
所以,点A′在该抛物线上.
(3)存在.理由:设直线CA′的解析式为y=kx+b,
则,解得
∴直线CA′的解析式为y=x+…(9分)
设点P的坐标为(x,x2﹣x﹣),则点M为(x,x+).
∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴(x+)﹣(x2﹣x﹣)=10.
解得x1=2,x2=5(不合题意,舍去)
当x=2时,y=﹣.
∴当点P运动到(2,﹣)时,四边形PACM是平行四边形.
2017年山东省济宁市中考数学试卷与答案: 这是一份2017年山东省济宁市中考数学试卷与答案,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2015年山东省济宁市中考数学试卷答案: 这是一份2015年山东省济宁市中考数学试卷答案,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2013年山东省济宁市中考数学试卷答案: 这是一份2013年山东省济宁市中考数学试卷答案,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












