（ 四年级 ）                                      备课教员：××× 

第13讲：相遇问题

一、教学目标：

1. 掌握相遇问题求路程的解题方法。

2. 熟练运用相遇公式解决未知量。

3. 时间和路程的思维转换，解决相遇问题。

4. 感受身边处处有数学，能够解决实际生活中的相遇问题。

二、教学重点：

1. 分析相遇问题的数量关系，解决相遇问题。

2. 通过观察、比较、分析，提高灵活解答的能力。

3. 学会借助线段图解题。

三、教学难点：

1. 时间和路程的思维转换，解决相遇问题。

2. 学会借助线段图解题。

四、教学准备：

PPT

五、教学过程：

第一课时（50分钟）

一、导入（5分)

师：同学们，上午好。

生：老师,上午好!

师：老师今天走路来学校差点就迟到了，你们都这么准时到学校，那你们是怎么来学校的呢？

生1：坐公交。

生2：家长开车送。

生3：……

师：看来同学们来学校的大多数都是坐车啊！那你们有没有发现一个奇怪的现象呢？

生：什么奇怪的现象？

师：你坐的车会和对面开过来车在路上遇到。

生：会，每天都会遇到很多次这种情况。

师：嗯，那你知道吗？在这个过程中还藏着一个数学问题呢！

生：什么数学问题？

师：这个呀就是我们今天要学习的相遇问题。

【PPT出示两车相遇的图片】

【板书课题：相遇问题】

二、探索发现授课（40分）

（一）例题1：（13分） 

两列火车同时从杭州和南京相对开出，甲列火车每小时行86千米，乙列火车每小时行102千米，经过5小时两车在途中相遇，求杭州到南京相距多少千米？

师：看到例题，这就是我刚才讲的相遇问题，你们先把题目读一读，分析分析题目，然后我们一起讨论。

【生读题，思考中】

师：好，停下来，我们一起看到题目，把你分析的结果说出来大家一起讨论分析。

生：两列火车从杭州和南京这两个地方同时发车，经过一定的时间这两列火车在途中相遇了。

师：嗯，请坐，还有不同的吗？

生：这两列火车，甲列火车是以每小时86千米的速度行驶，乙列火车是以每小时102千米的速度行驶，经过5小时在途中相遇。

师：嗯，两个人都不错，根据你们分析的情况，我们可以画出一幅线段图，假设线段的两端分别是杭州和南京并标注说明，线段的长度是杭州到南京的距离。那你们可以根据图将其他的信息标注上去吗？

板书：

生：根据图和题目的意思，分别将甲列火车和乙列火车写在杭州和南京的上面。

板书：

师：嗯，那这样就好了吗？

生：还有。要把速度和时间都加上去。

师：还有吗？可不可以说全啊！

生：我们还要把假设一个相遇点。

师：哇，真棒，既然把假设相遇点都说出来了，那现在看到这幅图，你们能把问题解决了吗？

板书：

生：能，杭州到南京的距离是甲列火车5小时行驶的路程加乙列火车5小时行驶的路程，列式是86×5＋102×5。

师：不错，但你们看，我们是不是可以把算式给简化呀！

生：可以，简化成（86＋102）×5。

师：嗯，很聪明，那把路程算出来吧！

生：（86＋102）×5=188×5=940（千米）

师：是的，所以杭州到南京的距离是940千米。那你们从这个例题中可以总结出一些解题方法吗？

生：在这个例题中，我知道了相遇路程=两车的速度和×相遇时间。

师：很好，但是有一点小不足，相遇一定是车吗？我们人不可以吗？

生：哦！相遇路程=速度和×相遇时间。

师：诶，这就比较好了，请坐。

板书：

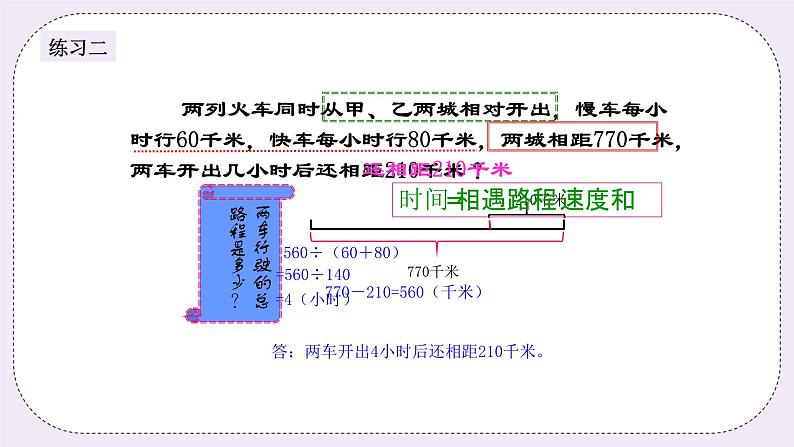
（86＋102）×5

=188×5

=940（千米）

答：杭州到南京的距离是940千米。

练习1：（6分）

     两艘军舰从相距609千米的两个港口同时相对开出，一艘军舰每小时行42千米，另一艘军舰每小时行45千米，经过几小时相遇？

分析：

要求相遇时间，应先求得两艘军舰的速度和，根据题意，速度和为42+45=87（千米/小时），然后用路程除以速度和即可求得相遇时间。

板书：

609÷（42+45）

   =609÷87

   =7（小时）

答：经过7小时相遇。

（二）例题2：（15分）

   甲、乙两列火车同时从相距450千米的两地相对开出，甲车每小时行45千米，5小时后两车还相距25千米，乙车每小时行多少千米？

师：同学们，经过前面的学习，相信这个例题对你们来说也不是特别难，你们先自己看题目，和同学轻声讨论，3分钟之后，我们汇集想法，一起解题，好吗？

生：好的。

【生讨论交流中，师巡视】

师：好，3分钟的时间到了，现在来说说你们的想法，每组选一个代表，哪组先来。

生1：题中告诉我们：两地之间的距离是450千米，甲车的速度是45千米每小时，5个小时后两车还相距25千米。

师：嗯，这是题目中告诉我们的条件，现在都已经找出来了，下一组能找一些不一样的吗？

生2：题中说5小时后还相距25千米，说明这时候两车还没有相遇，再根据前面的条件，我们可以画一幅线段图帮助我们理解题目。

师：嗯，不错，想到了借助线段图，那现在我们就根据题目的意思把线段图画出来吧！

师：首先，我们根据条件先用线段表示两地的距离，因为两车还没有相遇，两车之间还相差25千米，所以我们在两地之间的距离减掉一个25千米，也就说甲、乙两车实际上5小时是一共行驶了多少千米？

生：甲、乙两车5小时实际上是行驶了450－25=425（千米）。

师：嗯，看到线段图，我们又知道甲的速度和时间，那我们可不可以知道乙行驶的路程？

生：可以，乙车行驶的路程是425－45×5=200(千米）。

师：不错，乙车行驶的路程是200千米，但这是乙车几小时行驶的路程呢？1小时吗？

生：题中说了甲、乙两车同时出发，且经过5小时，所以甲、乙用的时间一样都是5小时。

师：哦，也就是说乙车5小时是行驶了200千米。那现在可以算出乙的速度吗？

生：可以，根据速度=路程÷时间，可以知道乙车的速度是200÷5=40（千米/小时）。

师：是的，乙车的速度是40千米/小时，同样的在做这个例题的过程中，你有什么发现，或者能总结出什么规律吗？

生：嗯，这是还没相遇的相遇问题，那在这个过程中，我们要先求出已经行驶的总路程，用两地距离减去还差的路程，是实际行驶的总路程，再根据条件求出一方在一定的时间内行驶的路程由路程=速度×时间算得，最后用实际行驶的总路程减去一方总路程再除以时间求得另一个的速度。

师：不错，我们要先算出一定时间内双方实际行驶的路程，然后根据路程=速度×时间算出其中一方行驶的总路程，最后算出另一方的总路程，再除以时间求得速度。

师：那记住咯，以后会经常用到，而且在生活中也可能会遇到哦！

板书：

     450-25=425（千米）          425-45×5   200÷5=40（千米/小时）
                                =425－225

                                =200（千米）

答：乙车每小时行40千米。

练习2：（8分）

    两列火车同时从甲、乙两城相对开出，慢车每小时行60千米，快车每小时行80千米，两城相距770千米，两车开出几小时后还相距210千米？

分析：

   要求两车开出几小时后还相距210千米？必须先求出两辆车行驶的总路程和速度和，两辆车行驶的总路程=770-210；速度和=60+80；然后解答即可。

板书：
    （770-210）÷（60+80）
    =560÷140
    =4（小时）

答：两车开出4小时后还相距210千米。

三、小结：（3分）

1. 相遇路程=速度和×相遇时间

2. 速度=路程÷时间

第二课时（50分）

一、复习导入（3分）

师：同学们，一节课过去，休息了一会儿，你们还能把上节课学过的知识准确无误地说出来吗？

生：老师，你又怀疑我们，肯定是能啦，不信说给你听。上节课我们学了相遇问题，相遇的路程=速度和×时间，还有一个是还差一点路程就相遇的题型，做这个题型最重要的是找出实际行驶的路程，然后根据速度=路程÷时间解题。

师：嗯，好，果然是老师小瞧你们了。那相信这节课你们肯定也能学得很好。

二、探索发现授课（42分）

（一）例题3：（13分）

    两港口相距267千米，客船以每小时45千米的速度、货船以每小时33千米的速度先后从两港开出，相向而行，相遇时客船行了135千米。货船比客船提前几小时开出？

师：同学们，看到这个题目好像比之前的要难好多哦，我们先一起读题，然后一起分析好吗？

生：好的。

师：读题之后，你们有什么发现吗？

生：客船和货船不是同一时间出发的。

师：哦，观察得可真仔细，一下子就被你发现了。是的，客船和货船不是同一时间出发。那又告诉了我们什么条件，要求的是什么？

生：告诉了两港口之间的距离，客船 、货船的速度，还告诉了客船行驶的总路程。

师：嗯，说得很好，那知道这些对我们解题有帮助吗？

生：由相遇时客船行驶的总路程和客船的速度，我们可以先把客船行驶的时间算出来。

师：哦，你们都同意这个想法吗？都同意，看来大家是越来越聪明了，那我们先把客船行驶的时间算出来吧！

师：客船行驶的时间是路程135千米除以速度每小时45千米等于3小时。

板书：

客船行驶的时间：135÷45=3（小时）

师：那好现在我们已经先把客船行驶时间算出来了，那货船的呢？我们好像只知道货船的速度吧！这可真难啊！

生：虽然题中只告诉了货船的速度，但是根据两港口相距267千米和相遇时客船行了135千米，可以算出货船行驶的总路程，然后算出货船行驶的时间。

师：你们果然都是认真学习的人，本来我还想故意为难你们呢！可现在轻而易举就被你们解决了，是的，货船行驶的总路程是两港口的距离减去客船行驶的路程，然后货船行驶时间是货船行驶的总路程除以货船的速度。列式是：

生（一起）：（267-135）÷33=4（小时）

板书：

（267-135）÷33=4（小时）

师：嗯，现在已经知道了客船和货船各自的行驶时间，那问题货船比客船提前几小时开出是不是很简单了。

生：用货船的行驶时间减去客船的行驶时间，4－3=1（小时）

师：嗯，很好，现在问题我们已经解决了。但你们都明白怎么做了吗？

生：明白了。

师：光说明白没用，得会做是不是，那把后面的练习完成吧！

板书：

    客船行驶的时间：135÷45=3（小时）

    货船行驶的路程：267-135=132（千米）

    货船行驶的时间：132÷33=4（小时）

    货船比客船提前开出：4-3=1（小时）

答：货船比客船提前1小时开出。

练习3：（7分）

    甲、乙两地相距384千米，两辆汽车从两地相对开出，甲车每小时行38千米，乙车每小时行42千米。甲车开出64千米后，乙车才出发，再经过几小时两车相遇？                                      

分析：

由条件甲车开出64千米后，乙车才出发，可以知道，甲、乙两车实际相遇路程是384－64=320（千米），再根据相遇路程=速度和×时间转换算出相遇时间。

板书：

     （384－64）÷（38＋42）

    ＝320÷80

＝4（小时） 

答：再经过4小时，两车相遇。

（二）例题4：（13分） 

    卡尔和阿派两人同时从相距2000米的两地相向而行，卡尔每分钟行110米，阿派每分钟行90米。如果一只狗与卡尔同时同向而行，狗每分钟跑500米，遇到阿派后，立即回头向卡尔跑去，遇到卡尔再向阿派跑去。这样不断来回跑，直到卡尔和阿派相遇为止，狗共跑了多少米？

师：同学们，先把题目读一遍，再说说你们发现了什么有趣的问题吗？

生：是卡尔和阿派在做一个相遇的运动，然后有一只狗一直在他们之间来回跑。

师：是的，看屏幕，是不是觉得很有趣，但是在这个有趣的过程中还有一个数学问题。

生：我知道，要求小狗一共跑了多少米。

师：是的，要求小狗一共跑了多少米。题中告诉了小狗的速度是每分钟跑500米，那时间有告诉吗？

生：没有。

师：那这个真有点难度，不过没关系，相信我们一定可以解决的。

师：我们分析题目，是卡尔和阿派两人同时从相距2000米的两地相向而行，而在他们相遇的时间内小狗在干嘛？

生：在卡尔和阿派相遇的时间内，小狗一直在他们俩之间跑来跑去。

师：是的，在卡尔和阿派相遇的时间内，小狗一直在他们俩之间跑来跑去。也就是说卡尔他们两人的相遇时间就是小狗跑步的时间。

师：可是卡尔他们相遇的时间又是多少呢？

生：卡尔他们的相遇时间是路程除以他们的速度和，2000÷（110＋90）=10（分钟）。

师：哦，越来越厉害了，是的卡尔他们相遇的时间是10分钟，也就是小狗跑了10分钟，所以小狗一共是跑了：500×10=5000（米）。

师：同学们，听明白了吗？

板书：

2000÷（110＋90）    500×10=5000（米） 

   =2000÷200

   =10（分钟）

答：狗共跑了5000米。

练习4：（7分）

   甲、乙两队学生从相隔18千米的两地同时出发相向而行。一个同学骑自行车以每小时15千米的速度在两队间不停地往返联络。甲队每小时行5千米，乙队每小时行4千米，两队相遇时，骑自行车的同学共行多少千米？

分析：

甲队每小时行5千米，乙队每小时行4千米，两地相距18千米，根据路程÷速度和=相遇时间可知两人相遇时共行了18÷（4+5）=2（小时），这两小时中，这名骑自行车的学生始终在运动，所以两队相遇时，骑自行车的学生共行：15×2=30（千米）。

板书：

      18÷（4+5）×15

     =18÷9×15

     =30（千米）

答：两队相遇时，骑自行车的学生共行了30千米。

（三）例题5（选讲）：

     甲地到乙地快车每小时行32千米，慢车每小时行18千米，如果两车同时从甲乙两地相对开出，可在距中点35千米的地方相遇，甲、乙两地相距多少千米？

师：先读题，再分析。

师：我们看到题目中在距中点35千米的地方相遇，看到这句话你们能想到什么？

生：……

师：一下子想不出来是不是，没关系，当我们画出线段图之后就比较好理解了。

板书：  

师：现在看到这幅图会不会觉得更容易理解呢？

生：嗯，但是这有什么关系呢？

师：别急，你看在图中是不是可以清楚地看出快、慢两车是在中点过去35千米处相遇的？

生：是的。

师：是快车行驶出中点35千米处与慢车相遇，那这时快车是比慢车多行驶多少千米，你知道吗？

生：快车比慢车多行驶35×2=70（千米），因为慢车只行驶了路程的一半－35千米，就可以知道快车行驶了路程的一半＋35千米，则快车是比慢车多行驶了35×2=70(千米)。

师：嗯，分析得很详细，很清楚。那这70千米是快车多长时间比慢车多行驶的呢？

生：……

师：我们看到题目中的条件“甲地到乙地快车每小时行32千米，慢车每小时行18千米”在这里我们可以知道什么？

生：快车和慢车的速度。

师：只能知道这些吗？

生：哦，我们还可以知道快车每小时比慢车快32－18=14（千米/小时）。

师：是的，现在知道快车比慢车一共多走了70千米，又知道快车每小时比慢车快14千米，那时间可不可以算出来呢？

生：可以，时间是70÷14=5（小时）。

师：不错，时间是5小时，这5小时同时也是快车与慢车相遇的时间，你们同意吗？

生：同意。

师：同意，那现在我们已经知道了快车、慢车的速度和两车相遇时间，那么甲、乙两地的距离是不是轻而易举就可以算出来了？

生（一起）：是的，甲、乙两地的距离是快车与慢车的速度之和乘相遇时间，（32＋18）×5=250（千米）。

师：是的，就这样简单的把问题给解决了，所以同学们以后做题一定要仔细分析条件，多利用条件去解决题目。

板书：

35×2=70（千米）     70÷（32－18）        （32＋18）×5

                    =70÷14                 =50×5

                    =5（小时）              =250（千米）

答：甲、乙两地相距250千米。

练习5：

    甲、乙两人同时从两地骑车相向而行，甲的速度是每小时20千米，乙每小时行18千米，两人在距离中点3千米的地方相遇。问两地相距多少千米？

分析：

本题与例题相似，在距离中点3千米的地方相遇，说明甲比乙多开了6千米，甲每小时比乙多开20－18＝2千米，那么6千米是有6÷2＝3（小时），知道时间后再根据相遇公式解答。

板书：

（3＋3）÷（20－18）  （20＋18）×3＝114（千米） 

 =6÷2                  

 =3（小时）             

答：两地相距114千米。

三、总结：（5分）

1. 相遇路程=速度和×相遇时间

2. 速度=路程÷时间

3. 时间=路程÷速度

四、随堂练习：

1. 欧拉和米德两人开车分别从相距480千米的A、B两城同时出发，相向而行，

   已知欧拉从A城到B城需6小时，米德从B城到A城需12小时，两人开车出

   发后多少小时相遇？

      欧拉的速度：480÷6=80（千米/小时）

      米德的速度：480÷12=40（千米/小时）

      相遇时间：480÷(80+40）=4（小时）

  答：两人开车出发后4小时相遇。

2.    A、B两地相距870千米，有两列火车同时从两站相对开出。甲车每小时行

   60 千米，乙车每小时比甲车快5千米，6小时后两车相距多少千米？

       （60＋5＋60）×6       870－750=120（千米）

        =（65＋60）×6

        =125×6

        =750（千米）

答：6小时后两车相距120千米。

3. 米德和欧拉同时从相距2360米的两地相向而行，欧拉每分钟走100米，米

   德每分钟走80米，相遇时米德走了960米。米德比欧拉晚出发多少分钟？

      米德行走的时间：960÷80=12（分钟）

      欧拉行走的路程：2360-960=1400（米）

      欧拉行走的时间：1400÷100=14（分钟）

      米德比欧拉晚出发：14-12=2（分钟）

  答：米德比欧拉晚出发2分钟。

4. A、B两地相距400千米，甲、乙两车同时从两地相对开出，甲车每小时行

   38千米，乙车每小时行42千米。一只燕子以每小时50千米的速度和甲车同

   时出发向乙车飞去，遇到乙车又折回向甲车飞去。这样一直往返地飞下去，

   燕子飞了多少千米后，两车才能相遇？

      400÷（38+42）

     =400÷80

     =5（小时）

     燕子飞行的距离：50×5=250（千米）

答：燕子飞了250千米后，两车才能相遇。

5. 甲、乙两辆汽车同时从东、西两地相向开出，甲车每小时行56千米，乙车

   每小时行48千米，两车在离中点32千米处相遇，求东、西两地的距离是多

   少千米？   

      32×2＝64（千米）    64÷（56－48）    （56＋48）×8

                            =64÷8             =104×8

                            =8（小时）         =832（千米）

答：东、西两地的距离是832千米。

家庭作业

主管评价

主管评分

课后反思

（不少于60字）

整体效果

设计不足之处

设计优秀之处