






奥数二年级上册寒假课程第3讲《一笔画成》课件+教案
展开(星星站) 备课教员:*** | |||
第三讲 一笔画成 | |||
一、教学目标: | 1.让学生体会用数学知识解决问题的方法。 2.通过其中抽象出点、线的过程,使学生对点、线有进一步的认识。 3.通过探究“一笔画成”的规律的活动,锻炼学生克服困难的意志及勇于发表见解的好习惯。 4.通过“一笔画成”问题及其结论的了解,扩大学生知识视野,激发学生学习兴趣。 | ||
二、教学重点: | 运用“一笔画成”的规律,快速正确地解决问题。 | ||
三、教学难点: | 探究“一笔画成”的规律。 | ||
四、教学准备: | PPT | ||
五、教学过程: 第一课时(40分钟) 一、外星游记(10分钟) 师:同学们,喜欢画画吗? 生:喜欢。 师:让老师看看你们画画的技术如何,每人画一幅画给老师看下好吗? 生:好。 师:但是老师有个小要求哦。 生:什么要求? 师:你们要画的这个图形很简单,只要画一个长方形就可以,要求是什么呢?要求就是你们在画这个长方形时笔不能离开纸,也就是要一笔画成这个图形,能做到吗? 生:能。 师:那让我们一起来挑战下,最先画完的小朋友将可以有奖励哦。 生:(一笔画长方形) 师:同学们都好厉害呢,都能一笔画成这个长方形,想不想挑战更难的? 生:想。 师:我们同桌两人为一组,一人戴上眼罩,另一人从老师手中随意抽出一张卡片,指挥蒙眼睛的同学(即笔不能离开纸)一笔画出这个图形,注意指挥者不能直接说这个图形是什么形,只能告诉蒙眼睛的同学画的路线或方向。3分钟内最先完成的一组将可以获得一次开宝箱的机会哦。(卡片中一笔画图形 ) (学生操作,老师巡视) 师:哪组小朋友完成了,并且画出来的图形跟卡片中是一样的? 生:(有或没有) 师:有的同学画出来了,有的同学却没画出来,老师相信这跟指挥官有很大的关系,如果他指挥你画的路线是正确的你肯定能画出这个图形,如果指挥你画的路线是错的,你肯定不能很顺利的一笔画出这个图形,所以今天老师就要教你们怎样一笔去画这样的图形。 (板书课题:一笔画成) | |||
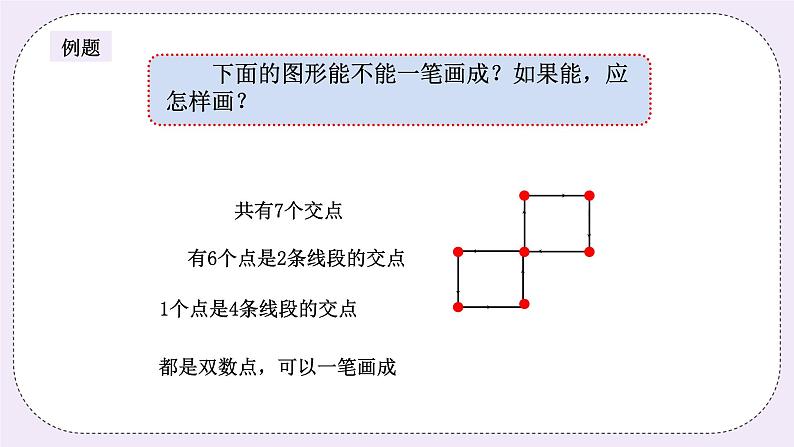
二、星海遨游(30分钟) (一)星海遨游1(10分钟) 下面的图形能不能一笔画成?如果能,应怎样画?
师:同学们,你们知道什么是一笔画成吗? 生:就是一笔画完这个图形。 师:对,一笔画成一个图形时,我们规定:1. 从图形上的某个点出发,笔不能离开纸;2. 每条线都只画一次,不能重复。同学们记住了吗? 生:记住了。 师:那同学们,请拿出你们的笔在这个图形上试着画一画看能不能一笔画的成,记住每条线都只能画一次哦。 (学生试着画图) 师:有没有哪位同学画好了。 生:我画好了。(这题图形不是很复杂,部分学生是可以一笔画成的) 师:你愿意上来把你的画法再呈现一次吗? 生:(上台板书)
师:画得真好,恭喜你一笔画成了这个图形。你能说说你在画的过程中有没有什么技巧呢? 生:(思考)有/没有。 师:还有哪些小朋友画成的?给每个画成的小朋友奖励2颗大拇指。 师:没有画成的小朋友是不是觉得一笔画成这样的图形特别复杂呢? 生:是的。 师:其实画这样一笔画成的图形一点都不难,它是有技巧的。你们想知道吗? 生:想。 师:在很早以前,著名的数学家欧拉就发现了一笔画成的规律:一个图能否一笔画成不在于图形是否复杂,也就是说不在于这个图包含多少个点和多少条线,而在于点和线的连接情况如何,最后他总结出:(板书或PPT出示) 1.凡是由双数点组成的连通图,一定可以一笔画成。画时可以把任一双数点作为起点,最后一定能以这个点作为终点画完此图。 2.凡是只有两个单数点的连通图(其余都为双数点),一定可以一笔画成。画时必须把一个单数点作为起点,另一个单数点作为终点。 3.其他情况的图都不能一笔画出。 师:那什么是双数点,什么是单数点呢? 生:不知道。 师:如果从一个点出发的线的总数是偶数(双数),称该点为双数点。如果从一个点出发的线的总数是奇数(单数),称该点为单数点。 师:那我们再来观察这个图形,这里有几个双数点,几个单数点? 生:7个双数点,0个单数点。 师:凡是由双数点组成的图能否一笔画成呢? 生:能。 师:对,可以把任一双数点作为起点,最后一定能以这个点作为终点画完此图。同学们再画一画看是不是真的这样。 生:(画图)是的。 师:只要我们掌握这一技巧,画一笔画成的图就不难了。 板书:
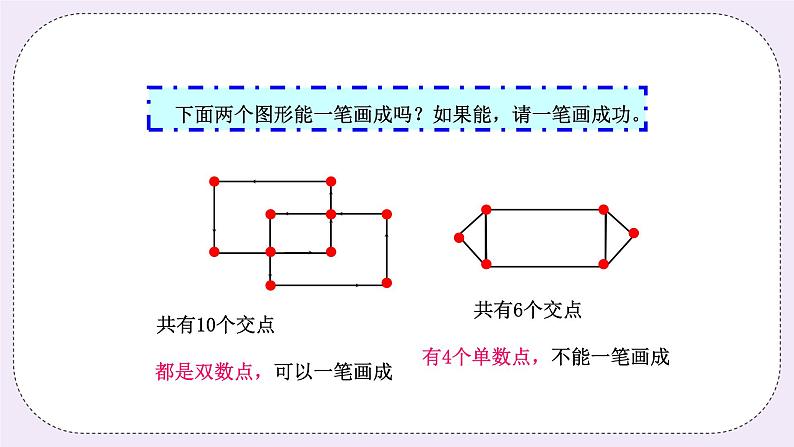
(一)星海历练1(5分钟) 下面两个图形能一笔画成吗?如果能,请一笔画成功。
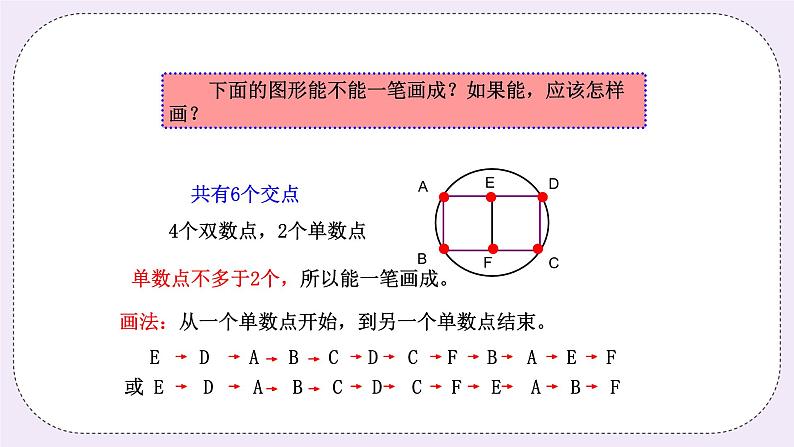
分析: 要判断图形是否能一笔画成,先判断这两个图形分别有多少个单数点,第一个图中共有10个交点,其中单数点有0个,都是双数点,可以一笔画成,把任一双数点作为起点,最后一定能以这个点作为终点画完此图。第二个图中共有6个交点,其中单数点有4个,单数点超过两个不能一笔画成。 板书: (二)星海遨游2(8分钟) 下面的图形能不能一笔画成?如果能,应该怎样画?
师:同学们,现在会判断图形能否一笔画成了吗? 生:会。 师:先要做什么? 生:看图形中有多少个单数点。 师:非常好,那让我们一起来数一数这个图形中有多少个单数点? 生1:一共有6个单数点。 生2:一共有2个单数点。 师:这题中同学们好像在数点数时有歧义哦,那让我们一起来判断下每个点是什么点吧,先看A点,这个点是什么点? 生1:是单数点。 生2:是双数点。 师:从这个点出发的线有几条? 生1:有3条。 生2:有4条。 师:对,有四条,A点出发有一条直线到B点,有一条直线到E点,还有一条曲线到B点及一条曲线到D点,所以它是双数点。明白了吗? 生:明白了。 师:那A、D、B、C这四个点都是什么点呢? 生:都是双数点。 师:那E、F又是什么点? 生:是单数点。 师:很好,所以说这个图形中单数点有几个? 生:有2个。 师:那能否一笔画成呢? 生:可以。 师:怎么画? 生:画时必须把一个单数点作为起点,另一个单数点作为终点。 师:真聪明,那同学们一起画一画吧。 板书: 画法:从一个单数点开始,到另一个单数点结束。 E D A B C D C F B A E F 或E D A B C D C F E A B F (二)星海历练2(5分钟) 下面的图形能不能一笔画成?如果能,应该怎样画?如果不能,请说明理由。
分析: 要判断图形是否能一笔画成,先判断这个图形有多少个单数点,图中共有9个交点,其中单数点有4个,单数点超过两个不能一笔画成。 板书: 图形不能一笔画成,因为图中单数点有4个,超过两个就不能一笔画成。 三、火星漫步(3分钟) 这节课我们学习了一笔画成,在解题时我们要记住什么是双数点和单数点,并且找出图形中有多少个双数点和单数点,都是双数 点的能一笔画成,单数点个数多于2个的不能一笔画成。 | |||
第二课时(40分钟) 一、外星游记(5分钟) 师:同学们,上节课我们学习了什么内容呢? 生:一笔画成。 师:要判断这个图形能否一笔画成,关键是看什么? 生:图中有几个单数点。 师:假设有4个单数点能不能一笔画成? 生:不能,只能有0个或2个单数点。 师:真聪明。 师:如果单数点有0个,或者说全是双数点时,以什么为起点? 生:以任一双数点为起点,最后一定能以这个点为终点画完此图。 师:如果单数点有2个,又该以什么为起点? 生:必须把一个单数点为起点,另一个单数点为终点。 师:那同学们都记住了吗? 生:记住了。 师:这节课我们再来研究一笔画成的路线。 | |||
二、太空遨游(30分钟) (一)太空遨游1(10分钟) 米德和卡尔在儿童乐园里玩,谁能不重复地走过所有的路?(线段代表路)
师:同学们,谁愿意帮老师读一读这个题目的? 生:我来。(学生读题) 师:同学们,思考下要不重复地走过所有的路,这可不可以把他们走的路线图看成是一笔画成图呢? 生:可以。 师:那我们要怎么做呢? 生:判断这个图中有多少个单数点。 师:那你们数一数,这题中有多少个单数点? 生:有2个单数点。 师:那是一笔画成的图吗? 生:是的。 师:有2个单数点时能一笔画成,起点应该从哪里画起? 生:画时必须以一个单数点为起点,另一个单数点为终点。 师:那米德的位置是不是单数点? 生:是单数点。 师:他能不重复的走过所有的路吗? 生:可以。 师:那卡尔的位置是不是单数点? 生:是双数点。 师:她能不重复的走过所有的路吗? 生:不能。 师:非常好,所以我们能判断出谁能不重复地走过所有的路呢? 生:米德。 板书: 米德能不重复地走过所有的路。 (一)太空探险1(5分钟) 阿派和妈妈分别从公园的两个入口进入,谁能一次不重复走完所有的路?
分析: 要判断阿派和妈妈能否不重复走完所有的路,也就是要判断这个路线图是否能一笔画成,先判断这个图形有多少个单数点,图中共有9个交点,其中单数点有2个,可以一笔画成,画时必须把一个单数点作为起点,另一个单数点作为终点。阿派的点是单数点,妈妈的点是双数点,所以阿派能一次不重复走完所有的路。 板书: 阿派能一次不重复地走完所有的路。 (二)太空遨游2(10分钟) 下面的图形中有6个单数点,因此不能一笔画成功。但只要给下图加两条直线,这个图形就能一笔画成功了。怎样加线?
师:同学们,通过前面的学习,我们知道只有几个单数点才能一笔画成呢? 生:2个。 师:那这题有6个单数点,如果我们要让这个图形能一笔画成,要把单数点变成几个呢? 生:变成2个。 师:也就是说我们要把其中4个单数点变成双数点,对吗? 生:对。 师:那我们来看下这6个单数点都在哪里。把它们标上。 生:(标单数点) 师:一个单数点怎样才能变成双数点呢? 生:加一条线。 师:那我们只能加两条线,所以这两条线应该加在哪? 生:每加一条线连接两个单数点,就可以减少两个单数点了。 师:真聪明,谁愿意上来帮老师画一画。 (学生上台板演) 师:画得真好。 板书:
(二)太空探险2(5分钟) 给下图加最少的直线,使这个图形能一笔画成功。
分析: 要能一笔画成,这个图形要不全是双数点,要不单数点只有2个,此图中,有4个单数点,需要减少2个单数点才能一笔画成。题中要求加最少的直线,因此连接任意两个单数点,至少需要加2条直线才能一笔画成。 板书:
三、火星漫步(5分钟) 一笔画成规律: ①可以一笔画成的图形,与双数点个数无关,与单数点个数有关。其个数是0个或2个。②其中若单数点个数为0,可选任一个点做起点,且一笔画后可以回到出发点。若单数点个数为2,可选其中一个单数点做起点,而终点一定是另一个单数点,即一笔画后不可以回到出发点。
四、决战太空城(见PPT) | |||
家庭作业: |
| ||
主管评价 |
| ||
主管评分 |
| ||
课后反思 (不少于60字) | 整体效果 |
| |
设计不足之处 |
| ||
设计优秀之处 |
| ||
奥数六年级上册寒假课程第3讲《分数的应用》课件+教案: 这是一份奥数六年级上册寒假课程第3讲《分数的应用》课件+教案,文件包含奥数六年级上册寒假课程第3讲《分数的应用》课件ppt、奥数六年级上册寒假课程第3讲《分数的应用》教案doc等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
奥数二年级上册寒假课程第7讲《认识简单数列》课件+教案: 这是一份奥数二年级上册寒假课程第7讲《认识简单数列》课件+教案,文件包含奥数二年级上册寒假课程第7讲《认识简单数列》课件ppt、奥数二年级上册寒假课程第7讲《认识简单数列》教案doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
奥数二年级上册寒假课程第6讲《简单推理》课件+教案: 这是一份奥数二年级上册寒假课程第6讲《简单推理》课件+教案,文件包含奥数二年级上册寒假课程第6讲《简单推理》课件ppt、奥数二年级上册寒假课程第6讲《简单推理》教案doc等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。













