福建省福州第一中学2023-2024学年九年级上学期开学考试数学试题

这是一份福建省福州第一中学2023-2024学年九年级上学期开学考试数学试题，共22页。
2023-2024学年福建省福州一中九年级（上）开学数学试卷
一．选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．（4分）在平面直角坐标系中，点（﹣2023，2024）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．（4分）化简的结果是（　　）
A．2 B．3 C．2 D．2
3．（4分）下列式子运算结果为2a的是（　　）
A．a•a B．2+a C．a+a D．a3÷a
4．（4分）如图，直线a∥b，∠1＝40°（　　）

A．30° B．40° C．50° D．60°
5．（4分）方程x2﹣x＝0的解是（　　）
A．x＝0 B．x＝1 C．x1＝0，x2＝1 D．x1＝0，x2＝﹣1
6．（4分）下列函数中，y随x的增大而增大的是（　　）
A．y＝ B．y＝﹣x+5
C．y＝x D．y＝（x＜0）
7．（4分）关于函数y＝﹣2x﹣4的图象，下列结论错误的是（　　）
A．过第二、三、四象限
B．与y轴的交点坐标为（0，﹣4）
C．经过点（1，2）
D．可由函数y＝﹣2x的图象平移得到
8．（4分）已知菱形的两条对角线长分别是6cm和8cm，则菱形的边长是（　　）
A．12cm B．10cm C．7cm D．5cm
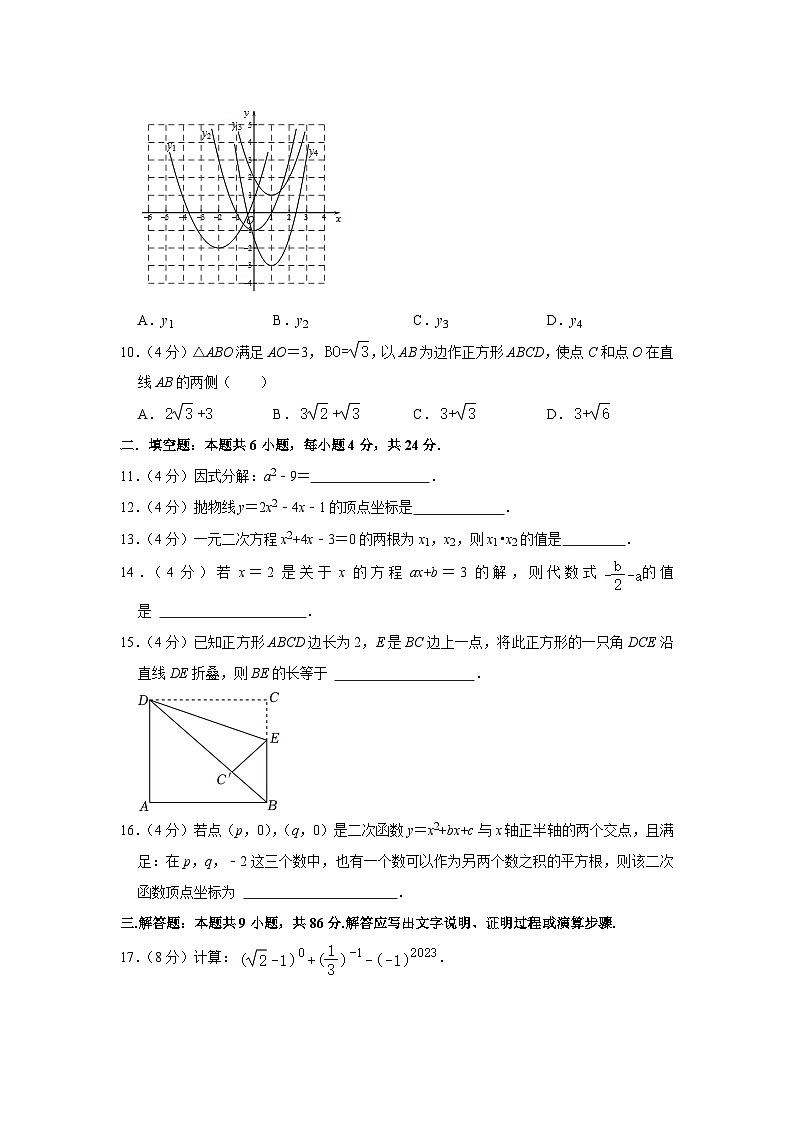
9．（4分）在平面直角坐标系xOy中，四条抛物线如图所示，其解析式中的二次项系数一定小于1的是（　　）

A．y1 B．y2 C．y3 D．y4
10．（4分）△ABO满足AO＝3，，以AB为边作正方形ABCD，使点C和点O在直线AB的两侧（　　）
A． B． C． D．
二．填空题：本题共6小题，每小题4分，共24分．
11．（4分）因式分解：a2﹣9＝　 　．
12．（4分）抛物线y＝2x2﹣4x﹣1的顶点坐标是　 　．
13．（4分）一元二次方程x2+4x﹣3＝0的两根为x1，x2，则x1•x2的值是　 　．
14．（4分）若x＝2是关于x的方程ax+b＝3的解，则代数式的值是 　 　．
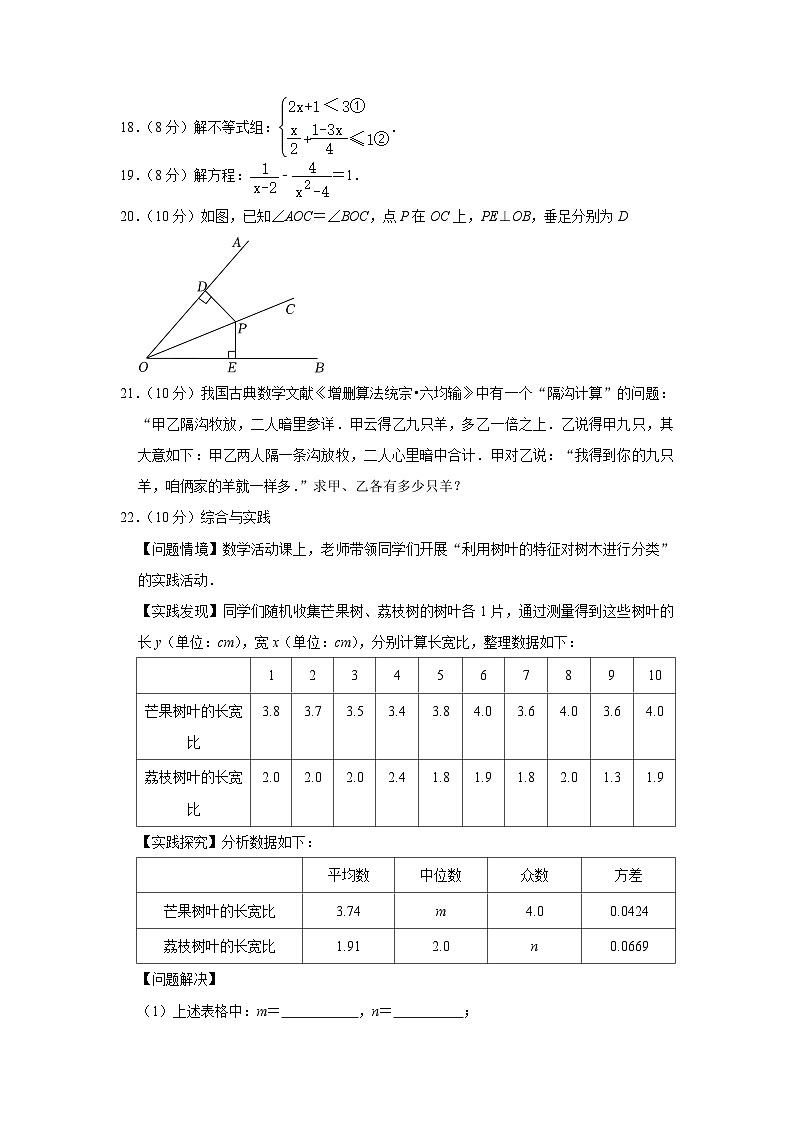
15．（4分）已知正方形ABCD边长为2，E是BC边上一点，将此正方形的一只角DCE沿直线DE折叠，则BE的长等于 　 　．

16．（4分）若点（p，0），（q，0）是二次函数y＝x2+bx+c与x轴正半轴的两个交点，且满足：在p，q，﹣2这三个数中，也有一个数可以作为另两个数之积的平方根，则该二次函数顶点坐标为 　 　．
三.解答题：本题共9小题，共86分.解答应写出文字说明、证明过程或演算步骤.
17．（8分）计算：．
18．（8分）解不等式组：．
19．（8分）解方程：﹣＝1．
20．（10分）如图，已知∠AOC＝∠BOC，点P在OC上，PE⊥OB，垂足分别为D

21．（10分）我国古典数学文献《增删算法统宗•六均输》中有一个“隔沟计算”的问题：“甲乙隔沟牧放，二人暗里参详．甲云得乙九只羊，多乙一倍之上．乙说得甲九只，其大意如下：甲乙两人隔一条沟放牧，二人心里暗中合计．甲对乙说：“我得到你的九只羊，咱俩家的羊就一样多．”求甲、乙各有多少只羊？
22．（10分）综合与实践
【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．
【实践发现】同学们随机收集芒果树、荔枝树的树叶各1片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm），分别计算长宽比，整理数据如下：

1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【实践探究】分析数据如下：

平均数
中位数
众数
方差
芒果树叶的长宽比
3.74
m
4.0
0.0424
荔枝树叶的长宽比
1.91
2.0
n
0.0669
【问题解决】
（1）上述表格中：m＝　 　，n＝　 　；
（2）①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大．”
②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍．”
上面两位同学的说法中，合理的是 　 　（填序号）；
（3）现有一片长11cm，宽5.6cm的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．

23．（10分）如图，四边形ABCD是正方形，点E，AB上，点H在BC的延长线上
（1）尺规作图：作出点M（与点D不重合），使其满足MF＝MH且∠FMH＝90°（要求：只保留作图痕迹，不写作法和证明）；
（2）连接（1）中的EM，猜想并写出四边形AFME是怎样的特殊四边形

24．（10分）如图1，在△ABC中，∠C＝90°，AD平分∠BAC交BC于D．
（1）求S△ABD：S△ACD的值；
（2）若S△ABD＝2+，求CD的长度；
（3）如图2，∠DAE＝90°，AD＝AE，判断BD和CM的数量关系并证明．

25．（12分）已知二次函数y＝ax2+（1﹣4a）x+3a﹣1（a＞）与x轴交于A（x1，0）、B（x2，0）两点（A在B的左侧），与y轴交于点C，顶点为点D．
（1）证明：函数图象与x轴正半轴有两个交点；
（2）无论a取何值，函数经过某（几）个定点．若定点与O、C两点构成的三角形中，求此时a的值；
（3）设直线BC与直线AD交于点M（m，n），求m，n满足的数量关系．

2023-2024学年福建省福州一中九年级（上）开学数学试卷
参考答案与试题解析
一．选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．（4分）在平面直角坐标系中，点（﹣2023，2024）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【分析】根据第二象限内点的坐标特点解答即可．
【解答】解：∵﹣2023＜0，2024＞0，
∴点（﹣2023，2024）在第二象限．
故选：B．
【点评】本题考查的是点的坐标，熟知各象限内点的坐标特点是解题的关键．
2．（4分）化简的结果是（　　）
A．2 B．3 C．2 D．2
【分析】将被开方数12写成平方数4与3的乘积，再将4开出来为2，易知化简结果为2．
【解答】解：＝5，
故选：A．
【点评】本题考查了二次根式的化简，关键在于被开方数要写成平方数乘积的形式再进行化简．
3．（4分）下列式子运算结果为2a的是（　　）
A．a•a B．2+a C．a+a D．a3÷a
【分析】直接利用同底数幂的乘除运算法则以及合并同类项法则分别判断得出答案．
【解答】解：A、a•a＝a2，故此选项不合题意；
B、2+a，故此选项不合题意；
C、a+a＝8a；
D、a3÷a＝a2，故此选项不合题意；
故选：C．
【点评】此题主要考查了同底数幂的乘除运算以及合并同类项，正确掌握相关运算法则是解题关键．
4．（4分）如图，直线a∥b，∠1＝40°（　　）

A．30° B．40° C．50° D．60°
【分析】利用平行线的性质可得结论．
【解答】解：∵a∥b，
∴∠2＝∠1＝40°．
故选：B．
【点评】本题考查了平行线的性质，掌握“两直线平行，同位角角相等”是解决本题的关键．
5．（4分）方程x2﹣x＝0的解是（　　）
A．x＝0 B．x＝1 C．x1＝0，x2＝1 D．x1＝0，x2＝﹣1
【分析】先分解因式，即可得出两个一元一次方程，求出方程的解即可．
【解答】解：x2﹣x＝0，
x（x﹣7）＝0，
x＝0，x﹣6＝0，
x1＝7，x2＝1，
故选：C．
【点评】本题考查了解一元二次方程，能把一元二次方程转化成一元一次方程是解此题的关键．
6．（4分）下列函数中，y随x的增大而增大的是（　　）
A．y＝ B．y＝﹣x+5
C．y＝x D．y＝（x＜0）
【分析】根据一次函数、反比例函数及二次函数的性质对各选项进行逐一分析即可．
【解答】解：A、∵函数y＝中，∴在每一象限内y随x增大而减小；
B、∵函数y＝﹣x+5中，∴y随x增大而减小；
C、∵函数y＝，k＝，∴y随x增大而增大；
D、∵函数y＝x5（x＜0）中，a＝，∴函数的开口向上，故本选项错误．
故选：C．
【点评】本题考查的是反比例函数、一次函数和二次函数的性质，熟知它们的增减性是解答此题的关键．
7．（4分）关于函数y＝﹣2x﹣4的图象，下列结论错误的是（　　）
A．过第二、三、四象限
B．与y轴的交点坐标为（0，﹣4）
C．经过点（1，2）
D．可由函数y＝﹣2x的图象平移得到
【分析】根据一次函数的性质对各选项进行逐一分析即可．
【解答】解：A、∵k＝﹣2＜0，∴图象经过第二、三，故结论正确；
B、∵当x＝5时，∴图象与y轴的交点坐标为（0，故结论正确；
C、∵当x＝1时，∴图象不经过点（3，故结论错误；
D、函数y＝﹣2x的图象向下平移4个单位得到y＝﹣2x﹣4，不合题意．
故选：C．
【点评】本题考查的是一次函数的性质，熟知一次函数y＝kx+b（k≠0），当k＜0，b＜0时函数图象经过二、三、四象限是解答此题的关键．
8．（4分）已知菱形的两条对角线长分别是6cm和8cm，则菱形的边长是（　　）
A．12cm B．10cm C．7cm D．5cm
【分析】根据菱形的性质求得OD，OA的长，再根据勾股定理求得边长AD的长．
【解答】解：如图：∵菱形ABCD中BD＝8cm，AC＝6cm，
∴OD＝BD＝4cmAC＝3cm，
在直角三角形AOD中AD＝＝＝7cm．
故选：D．

【点评】此题主要考查学生对菱形的性质及勾股定理的理解及运用．
9．（4分）在平面直角坐标系xOy中，四条抛物线如图所示，其解析式中的二次项系数一定小于1的是（　　）

A．y1 B．y2 C．y3 D．y4
【分析】先确定y2的二次项系数为1，然后根据二次项系数的绝对值大，图象开口反而小即可得出结论．
【解答】解：由图象可知：开口都是向上，二次项系数都大于01的开口最大，y3和y3的开口一样大，y4的开口最小，
∵抛物线y6的顶点为（0，﹣1），5）2＝x2﹣4，则二次项的系数为1，
故解析式中的二次项系数一定小于1的是y6
故选：A．
【点评】本题考查了二次函数的图象，二次函数的性质以及待定系数法求二次函数的解析式，根据点的坐标求得解析式是解题的关键．
10．（4分）△ABO满足AO＝3，，以AB为边作正方形ABCD，使点C和点O在直线AB的两侧（　　）
A． B． C． D．
【分析】证明△AOB≌△AQD（SAS），当点D、Q、O共线时，OD最大，即可求解．
【解答】解：将AO围绕点A逆时针旋转90°得到AQ，连接DQ、OD，

∵∠OAB+∠QAB＝90°，∠QAB+∠DAQ＝90°，
∴∠OAB＝∠QAD，
∵AO＝AQ，AB＝AD，
∴△AOB≌△AQD（SAS），
∴DQ＝OB＝3，
在等腰Rt△ADO中，OQ＝，
在△ODQ中，OD≤QD+OQ，
故当点D、Q、O共线时，
则OD＝OQ+DQ＝3+，
故选：D．
【点评】本题为正方形综合题，涉及到三角形全等、图形的旋转，确定点D、Q、O共线时，OD最大是解题的关键．
二．填空题：本题共6小题，每小题4分，共24分．
11．（4分）因式分解：a2﹣9＝　（a+3）（a﹣3）　．
【分析】a2﹣9可以写成a2﹣32，符合平方差公式的特点，利用平方差公式分解即可．
【解答】解：a2﹣9＝（a+4）（a﹣3）．
【点评】本题考查了公式法分解因式，熟记平方差公式的结构特点是解题的关键．
12．（4分）抛物线y＝2x2﹣4x﹣1的顶点坐标是　（1，﹣3）　．
【分析】将抛物线解析式配方成顶点式即可得出答案．
【解答】解：∵y＝2x2﹣5x﹣1＝2（x﹣5）2﹣3，
∴抛物线y＝4x2﹣4x﹣3的顶点坐标是（1，﹣3），
故答案为：（6，﹣3）．
【点评】本题主要考查二次函数的性质，解题的关键是熟练将抛物线的一般式配方成顶点式．
13．（4分）一元二次方程x2+4x﹣3＝0的两根为x1，x2，则x1•x2的值是　﹣3　．
【分析】根据根与系数的关系即可得出x1•x2＝﹣3，此题得解．
【解答】解：∵一元二次方程x2+4x﹣7＝0的两根为x1，x2，
∴x1•x2＝﹣3．
故答案为：﹣3．
【点评】本题考查了根与系数的关系，熟练掌握两根之积为是解题的关键．
14．（4分）若x＝2是关于x的方程ax+b＝3的解，则代数式的值是 　﹣　．
【分析】将x＝2代入原方程，可得出2a+b＝3，再将其代入﹣﹣a＝﹣（2a+b）中，即可求出结论．
【解答】解：将x＝2代入原方程得：2a+b＝2，
∴﹣﹣a＝﹣×8＝﹣．
故答案为：﹣．
【点评】本题考查了一元一次方程的解，牢记“把方程的解代入原方程，等式左右两边相等”是解题的关键．
15．（4分）已知正方形ABCD边长为2，E是BC边上一点，将此正方形的一只角DCE沿直线DE折叠，则BE的长等于 　4﹣2　．

【分析】根据正方形的性质得到CD＝2，BD＝2，∠EBD＝45°，根据折叠的性质得到DC′＝DC＝2，∠DC′E＝∠C＝90°，由等腰直角三角形的性质即可得到结论．
【解答】解：∵四边形ABCD是正方形，
∴CD＝2，BD＝2，
∵将此正方形的一只角DCE沿直线DE折叠，使C点恰好落在对角线BD上，
∴DC′＝DC＝2，∠DC′E＝∠C＝90°，
∴BC′＝2﹣2，
∴BE＝BC′＝7﹣2，
故答案为：2﹣2．
【点评】本题考查了翻折变换（折叠问题），正方形的性质，等腰直角三角形的性质，熟练掌握折叠的性质是解题的关键．
16．（4分）若点（p，0），（q，0）是二次函数y＝x2+bx+c与x轴正半轴的两个交点，且满足：在p，q，﹣2这三个数中，也有一个数可以作为另两个数之积的平方根，则该二次函数顶点坐标为 　（，﹣）　．
【分析】根据题意可以得出pq＝4①，＝q②或＝p③，联立①②或①③求出p，q的值，再用待定系数法求出二次函数解析式，再化为顶点式即可．
【解答】解：∵点（p，0），0）是二次函数y＝x3+bx+c与x轴正半轴的两个交点，
∴p＞0，q＞0，
∴﹣7是pq的平方根，
∴pq＝4①，
对称轴为直线x＝＞4，p，q，有一个数可以作为另两个数的平均数，
∴＝q②或，
由②得p＝2（q+6），
把p＝2（q+1）代入①并整理得：q5+q﹣2＝0
解得q7＝1，q2＝﹣3（舍去），
此时p＝4；
同理联立①③得p＝1，q＝8，
∴二次函数y＝x2+bx+c与x轴正半轴的两个交点为（1，4）和（4，
把（1，7）和（42+bx+c得：
，
解得，
∴二次函数解析式为y＝x6﹣5x+4＝（x﹣）2﹣，
∴顶点坐标为（，﹣）．
故答案为：（，﹣）．
【点评】本题考查抛物线与x轴的交点、二次函数的性质、二次函数图象上点的坐标特征，关键是求出抛物线与x轴的交点．
三.解答题：本题共9小题，共86分.解答应写出文字说明、证明过程或演算步骤.
17．（8分）计算：．
【分析】先计算零次幂、负整数指数幂和乘方，再计算加减．
【解答】解：
＝1+7+1
＝5．
【点评】此题考查了实数的混合运算能力，关键是能准确确定运算顺序和方法，并能进行正确地计算．
18．（8分）解不等式组：．
【分析】先求出每个不等式的解集，再根据“大小小大取中间”原则求出不等式组的解集即可．
【解答】解：解不等式①，得x＜1．
解不等式②，得x≥﹣3．
所以原不等式组的解集为﹣6≤x＜1．
【点评】本题主要考查了解一元一次不等式组，正确求出每个不等式的解集是解题的关键．
19．（8分）解方程：﹣＝1．
【分析】根据解分式方程的步骤：去分母、去括号、移项、合并同类项、系数化为1进行计算即可．
【解答】解：去分母得，x+2﹣4＝x5﹣4，
移项、合并同类项得，x2﹣x﹣3＝0，
解得x1＝7，x2＝﹣1，
经检验x＝6是增根，舍去，
所以原方程的根是x＝﹣1．
【点评】本题考查了解分式方程，熟记解分式方程的步骤：去分母、去括号、移项、合并同类项、系数化为1是解题的关键，注意验根．
20．（10分）如图，已知∠AOC＝∠BOC，点P在OC上，PE⊥OB，垂足分别为D

【分析】证明△POD≌△POE，根据全等三角形的性质证明结论．
【解答】证明：∵PD⊥OA，PE⊥OB，
∴∠PDO＝∠PEO＝90°，
在△POD和△POE中，
，
∴△POD≌△POE（AAS），
∴OD＝OE．
【点评】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理是解题的关键．
21．（10分）我国古典数学文献《增删算法统宗•六均输》中有一个“隔沟计算”的问题：“甲乙隔沟牧放，二人暗里参详．甲云得乙九只羊，多乙一倍之上．乙说得甲九只，其大意如下：甲乙两人隔一条沟放牧，二人心里暗中合计．甲对乙说：“我得到你的九只羊，咱俩家的羊就一样多．”求甲、乙各有多少只羊？
【分析】设甲有羊x只，乙有羊y只，根据甲对乙说：“我得到你的九只羊，我的羊就比你多一倍．”乙对甲说：“我得到你的九只羊，咱俩家的羊就一样多．”列出二元一次方程组，解方程组即可．
【解答】解：设甲有羊x只，乙有羊y只，
由题意得：，
解得：，
答：甲有羊63只，乙有羊45只．
【点评】本题考查了二元一次方程组的应用，找准等量关系，列出二元一次方程组是解题的关键．
22．（10分）综合与实践
【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．
【实践发现】同学们随机收集芒果树、荔枝树的树叶各1片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm），分别计算长宽比，整理数据如下：

1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【实践探究】分析数据如下：

平均数
中位数
众数
方差
芒果树叶的长宽比
3.74
m
4.0
0.0424
荔枝树叶的长宽比
1.91
2.0
n
0.0669
【问题解决】
（1）上述表格中：m＝　3.75　，n＝　2.0　；
（2）①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大．”
②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍．”
上面两位同学的说法中，合理的是 　②　（填序号）；
（3）现有一片长11cm，宽5.6cm的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．

【分析】（1）根据中位数和众数的定义解答即可；
（2）根据题目给出的数据判断即可；
（3）根据树叶的长宽比判断即可．
【解答】解：（1）把10片芒果树叶的长宽比从小到大排列，排在中间的两个数分别为3.7，故m＝；
10片荔枝树叶的长宽比中出现次数最多的是2.4，故n＝2.0；
故答案为：8.75；2.0；
（2）∵8.0424＜0.0669，
∴芒果树叶的形状差别小，故A同学说法不合理；
∵荔枝树叶的长宽比的平均数1.91，中位数是2.95，
∴B同学说法合理．
故答案为：②；
（3）∵11÷5.6≈6.96，
∴这片树叶更可能是荔枝树叶．
【点评】本题考查了众数，中位数，平均数和方差，掌握相关定义是解答本题的关键．
23．（10分）如图，四边形ABCD是正方形，点E，AB上，点H在BC的延长线上
（1）尺规作图：作出点M（与点D不重合），使其满足MF＝MH且∠FMH＝90°（要求：只保留作图痕迹，不写作法和证明）；
（2）连接（1）中的EM，猜想并写出四边形AFME是怎样的特殊四边形

【分析】（1）根据正方形的性质作图；
（2）根据矩形和平行四边形的判定定理进行证明．
【解答】解：（1）如图：分别以F，H为圆心，两弧相交于点M，
点M即为所求；
（2）四边形AFME是平行四边形；
证明：连接FH，
∵四边形ABCD是正方形，
∴∠DAB＝∠B＝∠BCD＝∠ADC＝90°，AB＝BC＝CD＝DA，
∵AF＝BE＝CH，
∴△ABE≌△DAF≌△DCH（SAS），
∴DF＝AE＝DH，∠H＝∠AEB，
∴AE∥DH，∠FDH＝90°，
∴∠DFH＝∠DHF＝45°，
∵MF＝MH，∠FMH＝90°，
∴∠MFH＝∠FHM＝45°，
∴∠DFM＝∠DHM＝∠M＝90°，
∴四边形DFMH为矩形，
∵MF＝DH，MF∥DH，
∴AE∥FM，AE＝FM，
∴四边形AFME为平行四边形．

【点评】本题考查了复杂作图，掌握矩形的判定定理和性质及平行四边形的判定定理是解题的关键．
24．（10分）如图1，在△ABC中，∠C＝90°，AD平分∠BAC交BC于D．
（1）求S△ABD：S△ACD的值；
（2）若S△ABD＝2+，求CD的长度；
（3）如图2，∠DAE＝90°，AD＝AE，判断BD和CM的数量关系并证明．

【分析】（1）过点D作DE⊥AB于点E，根据角平分线的性质得DE＝CD，然后利用三角形的面积即可解决问题；
（2）设CD＝DE＝x，由△DBE是等腰直角三角形，得BE＝DE＝x，所以BD＝x，得AC＝BC＝x+x，然后证明Rt△ACD≌Rt△AED（HL），得AC＝AE＝x+x，然后利用三角形的面积求出x的值，即可解决问题；
（3）过点E作EF⊥AC于点F，证明△AEF≌△DAC（AAS），根据全等三角形的性质得EF＝AC，AF＝DC，推出CF＝BD，再证△BCM≌△EFM （AAS），根据全等三角形的性质得CM＝FM＝CF，可得CF＝2CM，即BD＝2CM．
【解答】解：（1）在△ABC中，
∵∠C＝90°，AC＝BC，
∴∠B＝45°，AB＝，
如图1，过点D作DE⊥AB于点E，

∵AD平分∠BAC，∠C＝90°，
∴DC⊥AC，∠AED＝∠C＝90°，
∴DE＝CD，
∴S△ABD：S△ACD＝（AB•DE）：（AC：AC＝，
∴S△ABD：S△ACD的值为；
（2）设CD＝DE＝x，
∵DE⊥AB，∠B＝45°，
∴△DBE是等腰直角三角形，
∴BE＝DE＝x，
∴BD＝x，
∴AC＝BC＝CD+BD＝x+x，
∵AD＝AD，CD＝ED，
∴Rt△ACD≌Rt△AED（HL），
∴AC＝AE＝x+x，
∴AB＝AE+BE＝x+x+x＝2x+）x，
∵S△ABD＝2+，
∴AB•DE＝，
∴（2+，
∴x＝（负值舍去），
∴CD的长度为；
（3）BD＝2CM，
证明：如图2，过点E作EF⊥AC于点F，

∴∠AFE＝∠CFE＝90°，
∴∠AEF+∠EAF＝90°，
∵∠DAE＝90°，
∴∠EAF+∠DAC＝90°，
∴∠AEF＝∠DAC，
在△AEF和△DAC中，
，
∴△AEF≌△DAC（AAS），
∴EF＝AC，AF＝DC，
∵AC＝BC，
∴EF＝BC，AC﹣AF＝BC﹣DC，
∴CF＝BD，
在△BCM和△EFM中，
，
∴△BCM≌△EFM（AAS），
∴CM＝FM＝CF，
∴CF＝2CM，
∴BD＝5CM．
【点评】此题是三角形综合题，主要考查了全等三角形的判定和性质，勾股定理，等腰直角三角形的性质，角平分线的性质，利用全等三角形的判定和性质是解本题的关键．
25．（12分）已知二次函数y＝ax2+（1﹣4a）x+3a﹣1（a＞）与x轴交于A（x1，0）、B（x2，0）两点（A在B的左侧），与y轴交于点C，顶点为点D．
（1）证明：函数图象与x轴正半轴有两个交点；
（2）无论a取何值，函数经过某（几）个定点．若定点与O、C两点构成的三角形中，求此时a的值；
（3）设直线BC与直线AD交于点M（m，n），求m，n满足的数量关系．
【分析】（1）依据题意，由y＝ax2+（1﹣4a）x+3a﹣1＝（x﹣1）（ax﹣3a+1），令y＝0即可得出与x轴交点的坐标，再结合题意，可以得解；
（2）依据题意，任取a＝1，a＝2，进而建立关于x，y的方程组从而计算可以得解；
（3）依据题意，求出直线BC与直线AD的交点M，再消去a，即可得解．
【解答】（1）证明：由y＝ax2+（1﹣2a）x+3a﹣1＝（x﹣6）（ax﹣3a+1），令y＝5，
∴x＝1或x＝．
∵a＞，
∴＜2．
∴3﹣＞1．
∴x＝＞1．
∵抛物线与x轴交于A（x1，3）、B（x2，0）两点（A在B的左侧），
∴A（5，0），0）．
∴函数图象与x轴正半轴有两个交点．
（2）解：由题意，任取a＝1，进而建立关于x，
∴或．
∴抛物线过定点A（1，4），2）．
定点与O、C两点构成的三角形中，
∴可分以下两种情形：
①O、C（0，A（5，
此时是直角三角形，只有OA＝OC，
∴3a﹣1＝8．
∴a＝．
②O、C（6，E（3，
存在以下可能，
当OC＝OE时，OC＝OE＝3a﹣8＝，
∴a＝；
当OC＝CE时，依据勾股定理5＝（OC﹣2）2+52，
∴OC＝3a﹣8＝．
∴a＝．
当OE＝CE时，
∴OC＝3a﹣3＝4．
∴a＝．
综上，a＝或或或．
（3）解：由题意，B（，C（5，
∴直线BC为：y＝﹣ax+3a﹣1．
∵A（2，0），﹣），
∴直线AD为：y＝（x﹣6）．
∴直线BC与直线AD的交点M满足它们的解析式组成的方程组．
∴m＝4a﹣1，n＝﹣（5a﹣1）2．
∴n＝﹣（3×﹣6）2．
∴n＝﹣（m﹣1）2．
【点评】本题主要考查了抛物线的图象与性质、等腰三角形的性质，解题时要熟练掌握并能灵活运用是关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/9/21 17:23:08；用户：娄老师；邮箱：15225657626；学号：48669677