山东省鄄城县第一中学2022-2023学年高一下学期4月月考数学试题

高一数学试题

一、单选题（本题共8小题，每题5分，共40分）

1．在下列条件下，能确定一个平面的是（    ）

A．空间的任意三点  B．空间的任意一条直线和任意一点

C．空间的任意两条直线 D．梯形的两条腰所在的直线

2．如图为水平放置的直观图，其中，，那么原的面积是（    ）

A． B． C． D．2

3．在复平面内，复数，对应的点分别是，，则的虚部是（    ）

A．i B．-i C．1 D．-1

4．在中，，则的形状是（    ）

A．锐角三角形 B．钝角三角形 C．直角三角形 D．不能确定

5．已知，为单位向量，向量满足．若与的夹角为60°，则（    ）

A． B． C． D．3

6．如图，已知圆锥的底面半径为1，母线长，一只蚂蚁从A点出发绕着圆锥的侧面爬行一圈回到点A，则蚂蚁爬行的最短距离为（    ）

A． B． C．6 D．2π

7．点P在内部，满足，则为（    ）

A．2∶1 B．3∶1 C．3∶2 D．5∶3

8．古希腊数学家帕普斯在《数学汇编》第三卷中记载着一个确定重心的定理：“如果同一平面内的一个闭合图形的内部与一条直线不相交，那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以该闭合图形的重心旋转所得周长的积”，即（V表示平面图形绕旋转轴旋转的体积，S表示平面图形的面积，l表示重心绕旋转轴旋转一周的周长）．已知中，，，，则的重心G到AC的距离为（    ）

A． B． C．1 D．2

二、多选题（本题共4小题，每题5分，共20分）

9．下面关于空间几何体的叙述正确的是（    ）

A．底面是正多边形的棱锥是正棱锥 B．用平面截圆柱得到的截面只能是圆和矩形

C．长方体是直平行六面体 D．存在每个面都是直角三角形的四面体

10．下列选项中，错误的是（    ）

A．若存在实数λ使成立，则与共线

B．若，则

C．若（M、A、B、C四点不同），则A、B、C三点共线

D．若，则或

11．已知中，其内角A，B，C的对边分别为a，b，c下列命题正确的有（    ）

A．若，则

B．若，，则外接圆半径为10

C．若，则为等腰三角形

D．若，，，则

12．若a，b是空间中两条直线，平面α，空间点A，则下列结论正确的是（    ）

A．若，则或a与α相交 B．若，，则a，b无公共点

C．若，，则 D．若，则

三、填空题（本题共4小题，每题5分，共20分）

13．已知，且，则复数______．

14．已知单位向量，，且，则______．

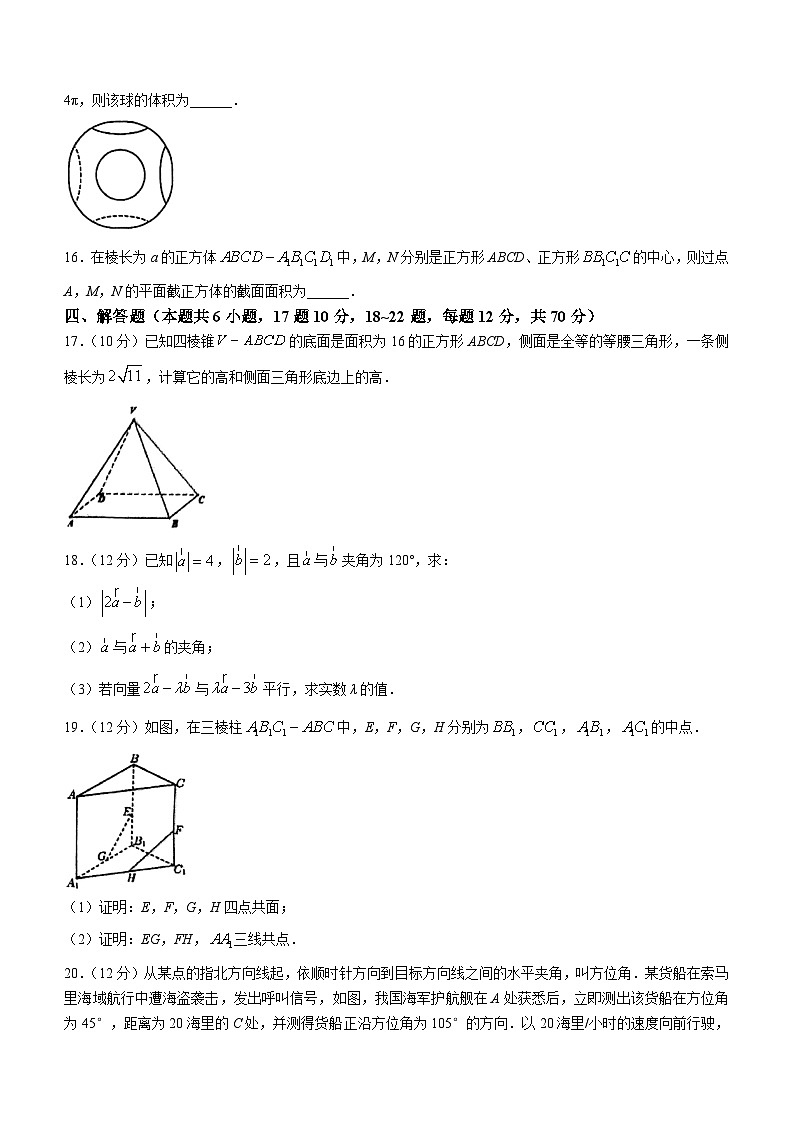
15．某同学在参加《通用技术》实践课时，制作了一个工艺品，如图所示，该工艺品可以看成是一个球被一个棱长为的正方体的六个面所截后剩余的部分（球心与正方体的中心重合），若其中一个截面圆的周长为4π，则该球的体积为______．

16．在棱长为a的正方体中，M，N分别是正方形ABCD、正方形的中心，则过点A，M，N的平面截正方体的截面面积为______．

四、解答题（本题共6小题，17题10分，18~22题，每题12分，共70分）

17．（10分）已知四棱锥的底面是面积为16的正方形ABCD，侧面是全等的等腰三角形，一条侧棱长为，计算它的高和侧面三角形底边上的高．

18．（12分）已知，，且与夹角为120°，求：

（1）；

（2）与的夹角；

（3）若向量与平行，求实数λ的值．

19．（12分）如图，在三棱柱中，E，F，G，H分别为，，，的中点．

（1）证明：E，F，G，H四点共面；

（2）证明：EG，FH，三线共点．

20．（12分）从某点的指北方向线起，依顺时针方向到目标方向线之间的水平夹角，叫方位角．某货船在索马里海域航行中遭海盗袭击，发出呼叫信号，如图，我国海军护航舰在A处获悉后，立即测出该货船在方位角为45°，距离为20海里的C处，并测得货船正沿方位角为105°的方向．以20海里/小时的速度向前行驶，我海军护航舰立即以海里/小时的速度，以直线轨迹行驶前去营救，求护航舰的航向（方位角）和靠近货船所需的时间．

21．（12分）如图，在水平放置的直径与高相等的圆柱内，放入两个半径相等的小球（球A和球B），圆柱的底面直径为，向圆柱内注满水，水面刚好淹没小球B．

（1）求球A的体积；

（2）求圆柱的侧面积与球B的表面积之比．

22．（12分）在锐角中，内角A，B，C的对边分别为a，b，c，且满足．

（1）求角C的大小；

（2）求的取值范围．

高一数学答案

1-5．DADDB    6-8．BBB    9．CD    10．BD    11．ACD    12．AD

三、填空题

13．    14．

15．【解析】球被正方体的面所截小圆半径，而球心到截面小圆距离为，因此该球的半径，所以该球的体积．

16．  【解析】如图连接AC，则AC过点M，连接，则经过点N，连接，则过点A、M、N的平面截正方体的截面为等边，因为正方体棱长为a，故边长为，面积为．

四、解答题（本题共6小题，17题10分，18~22题，每题12分，共70分）

17．如下图所示：作VO为四棱锥的高，

作于点M，则M为BC的中点．连接OB，则，．

∵底面正方形ABCD的面积为16，∴，．

则．

又，在中，由勾股定理，可得

．

在中，由勾股定理，可得，

即四棱锥的高为6，侧面三角形底边上的高为．

18．解：（1）因为，所以；

（2）因为，所以，

又，

所以，所以与的夹角为．

（3）因为向量与平行，所以，

因为向量与不共线，所以，解得．

19．（1）如图，连接EF，GH．

∵GH是的中位线，∴．

∵，且，∴四边形是平行四边形，

∴，∴，∴E，F，G，H四点共面．

（2）如图，延长EG，FH相交于点P．

∵，平面，∴平面．

∵，平面，∴平面

∵平面平面，∴，∴EG，FH，三线共点．

20．解：设护航舰靠近货船所需时间为t小时，营救地点为B，可得，．

在中，由余弦定理可得，

∴，化简可得，

∴或（舍去）

∴护航舰需要1小时靠近货船。∴，，

在中，根据正弦定理得：，

∴，为三角形内角．

∴，∴可得护航舰航行的方位角为75°，所需时间为1小时．

21．解（1）设圆柱的底面半径为R，小球的半径为r，且，

由圆柱与球的性质知，

即，

∵，∴．

∴球A的体积为

（2）球B的表面积，

圆柱的侧面积，

∴圆柱的侧面积与球B的表面积之比为．

22．（1），整理得，

故，又，所以；

（2）由锐角知，，得，

故

因为，，得，

所以．