人教B版 (2019)选择性必修 第一册1.2.2 空间中的平面与空间向量同步达标检测题

第一章1.2.2　空间中的平面与空间向量

A级 必备知识基础练

1.[探究点一]若a=(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是(　　)

A.(0,1,2) B.(3,6,9)

C.(-1,-2,3) D.(3,6,8)

2.[探究点二(角度1)]设平面α的法向量为(1,-2,λ),平面β的法向量为(2,μ,4),若α∥β,则λ+μ=(　　)

A.2 B.4 

C.-2 D.-4

3.[探究点二(角度1)]已知n为平面α的一个法向量,l为一条直线,则“l⊥n”是“l∥α”的(　　)

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

4. [探究点二]如图,在长方体ABCD-A1B1C1D1中,E,F分别是棱BB1,B1C1的中点,以下说法正确的是(　　)

A.A1E∥平面CC1D1D

B.A1E⊥平面BCC1B1

C.A1E∥D1F

D.A1E⊥D1F

5.[探究点二](多选题)下列利用方向向量、法向量判断线、面位置关系的结论中,正确的是(　　)

A.若两条不重合的直线l1,l2的方向向量分别是a=(2,-2,-1),b=(-2,-2,1),则l1∥l2

B.若直线l的方向向量是a=(1,1,2),平面α的一个法向量是n=(-2,-2,-4),则l⊥α

C.若直线l的方向向量是a=(0,2,0),平面α的一个法向量是n=(-2,0,2),则l∥α

D.若两个不同的平面α,β的法向量分别是m=(3,-4,2),n=(-2,0,3),则α⊥β

6.[探究点二(角度2)]已知直线l与平面α垂直,直线l的一个方向向量u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z=　　　　. 

7.[探究点二(角度1)]若=λ+μ(λ,μ∈R),则直线AB与平面CDE的位置关系是　　　　　　. 

8.[探究点二·2023广东佛山高二阶段练习]若平面α的一个法向量为m=(2,-6,s),平面β的一个法向量为n=(1,t,2),且α∥β,则s-t=　　　　　. 

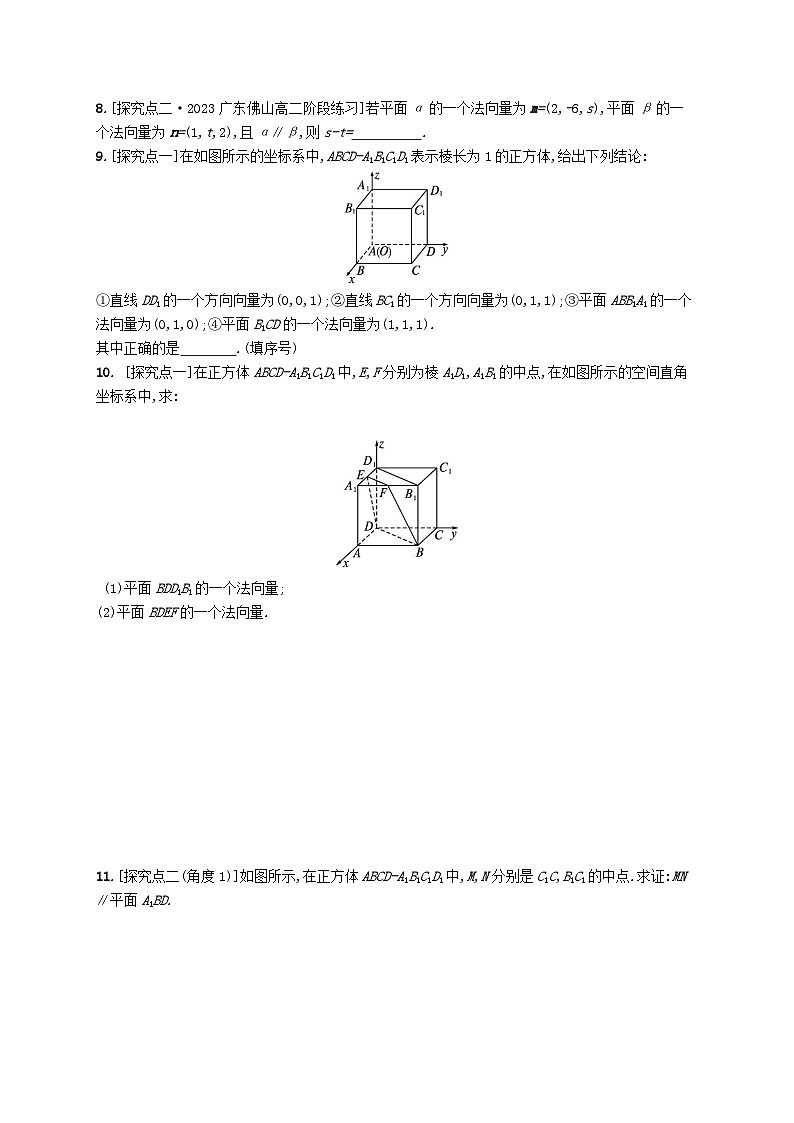
9.[探究点一]在如图所示的坐标系中,ABCD-A1B1C1D1表示棱长为1的正方体,给出下列结论:

①直线DD1的一个方向向量为(0,0,1);②直线BC1的一个方向向量为(0,1,1);③平面ABB1A1的一个法向量为(0,1,0);④平面B1CD的一个法向量为(1,1,1).

其中正确的是　　　　.(填序号) 

10. [探究点一]在正方体ABCD-A1B1C1D1中,E,F分别为棱A1D1,A1B1的中点,在如图所示的空间直角坐标系中,求:

 (1)平面BDD1B1的一个法向量;

(2)平面BDEF的一个法向量.

11.[探究点二(角度1)]如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.

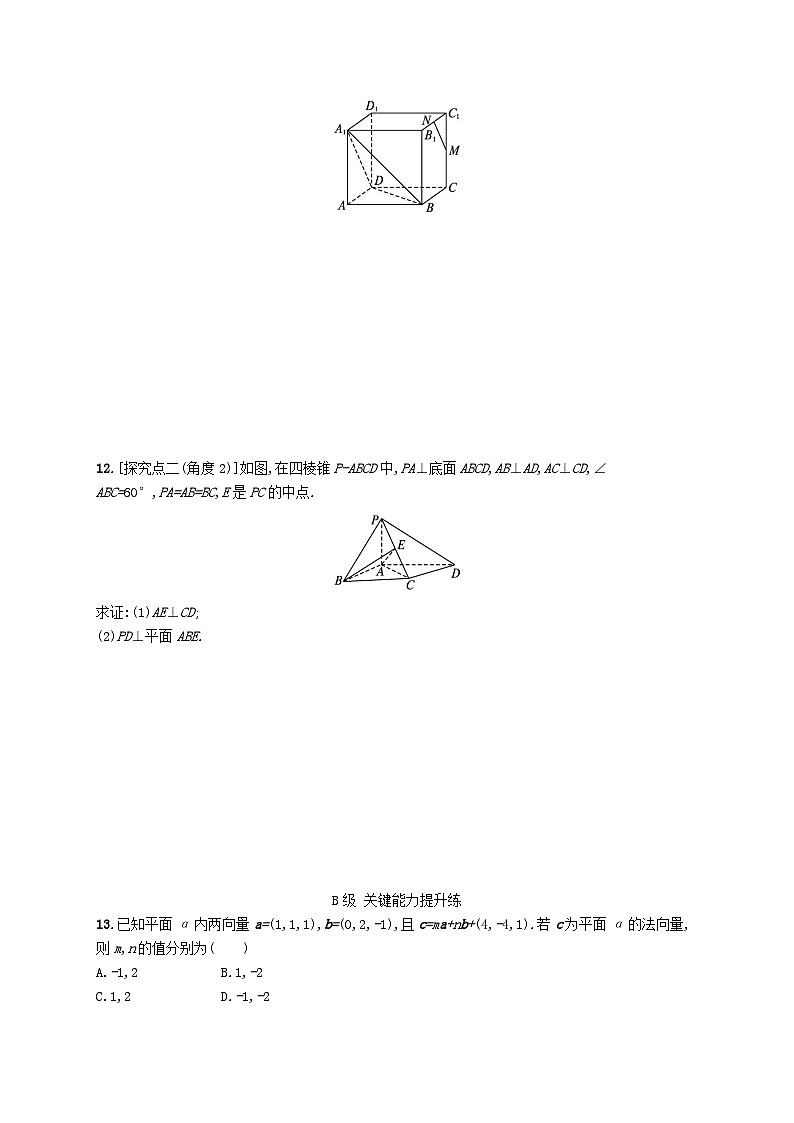
12.[探究点二(角度2)]如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.

求证:(1)AE⊥CD;

(2)PD⊥平面ABE.

B级 关键能力提升练

13.已知平面α内两向量a=(1,1,1),b=(0,2,-1),且c=ma+nb+(4,-4,1).若c为平面α的法向量,则m,n的值分别为(　　)

A.-1,2 B.1,-2

C.1,2 D.-1,-2

14.已知直线l的方向向量为a,且直线l不在平面α内,平面α内两共点向量,下列关系中一定能表示l∥α的是(　　)

A.a= B.a=k

C.a=p+λ D.以上均不能

15.[2023河南商城高二阶段练习]已知直线l的方向向量是a=(3,2,1),平面α的法向量是u=(-1,2,-1),则l与α的位置关系是(　　)

A.l⊥α  B.l∥α

C.l与α相交但不垂直 D.l∥α或l⊂α

16.[2023广东佛山高二阶段练习]已知两个不重合的平面α与平面ABC,若平面α的法向量为n1=(2,-3,1),向量=(1,0,-2),=(1,1,1),则(　　)

A.平面α∥平面ABC

B.平面α⊥平面ABC

C.平面α,平面ABC相交但不垂直

D.以上均有可能

17.[2023浙江玉环高二阶段练习](多选题)已知点P是平行四边形ABCD所在的平面外一点,如果=(2,-1,-4),=(4,2,0),=(-1,2,-1),下列结论正确的有(　　)

A.

B.

C.是平面ABCD的一个法向量

D.

18.如图,在长方体ABCD-A1B1C1D1中,AB=4,BC=2,CC1=3,E,F分别是BC,CD的中点,以D为原点,分别以DA,DC,DD1所在直线为坐标轴建立空间直角坐标系,则平面D1EF的一个法向量是　　　　　. 

19.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量n与平面ABC垂直,且|n|=,则n的坐标为　　　　. 

C级 学科素养创新练

20. 如图所示,平面CDEF⊥平面ABCD,且四边形ABCD为平行四边形,∠DAB=45°,四边形CDEF为直角梯形,EF∥DC,ED⊥CD,AB=3EF=3,ED=a,AD=.

 (1)求证:AD⊥BF;

(2)若线段CF上存在一点M,满足AE∥平面BDM,求的值.

1.2.2　空间中的平面与空间向量

1.B　向量(1,2,3)与向量(3,6,9)共线.

2.C　∵α∥β,

∴,解得λ=2,μ=-4,∴λ+μ=-2.

3.B　当“l⊥n”时,由于l可能在平面α内,所以无法推出“l∥α”;

当“l∥α”时,“l⊥n”.

综上所述,“l⊥n”是“l∥α”的必要不充分条件.故选B.

4.A　由长方体的性质有平面ABB1A1∥平面CC1D1D,又A1E⊂平面ABB1A1,所以A1E∥平面CC1D1D,故选项A正确;

因为E为棱BB1的中点,且A1B1⊥BB1,所以A1E与BB1不垂直,

所以若A1E⊥平面BCC1B1,则A1E⊥BB1,这与A1E和BB1不垂直相矛盾,故选项B错误;

以D为坐标原点,建立如图所示的空间直角坐标系.

设DA=a,DC=b,DD1=c,则A1=(a,0,c),E(a,b,),D1(0,0,c),F(,b,c),

所以=(0,b,-),=(,b,0).

因为不是共线向量,且=b2>0,

所以A1E与D1F不平行,且A1E与D1F不垂直,故选项C,D错误.

故选A.

5.BD　对于A,因为向量a,b不平行,所以l1,l2不平行,故A不正确;

对于B,因为n=-2a,所以a∥n,故B正确;

对于C,因为a·n=0×(-2)+2×0+0×2=0,所以a⊥n,所以l∥α或l⊂α,故C不正确;

对于D,因为m·n=-6+0+6=0,所以α⊥β,故D正确.

故选BD.

6.-9　由题知,u⊥v,∴u·v=3+6+z=0,∴z=-9.

7.AB∥平面CDE或AB⊂平面CDE

8.7　由α∥β,得m∥n,易知t,s≠0,∴,解得t=-3,s=4,

∴s-t=7.

9.①②③　DD1∥AA1,=(0,0,1),故①正确;BC1∥AD1,=(0,1,1),故②正确;直线AD⊥平面ABB1A1,=(0,1,0),故③正确;点C1的坐标为(1,1,1),与平面B1CD不垂直,故④错误.

10.解设正方体ABCD-A1B1C1D1的棱长为2,

则D(0,0,0),B(2,2,0),D1(0,0,2),E(1,0,2).

(1)设平面BDD1B1的一个法向量为n=(x1,y1,z1).

∵=(2,2,0),=(0,0,2),

∴

令x1=1,则y1=-1,z1=0,

∴平面BDD1B1的一个法向量为n=(1,-1,0).

(2)=(2,2,0),=(1,0,2).

设平面BDEF的一个法向量为m=(x2,y2,z2),

则

令x2=2,则y2=-2,z2=-1,

∴平面BDEF的一个法向量为m=(2,-2,-1).

11.证明(方法一)∵)=,

∴,

又MN⊄平面A1BD,∴MN∥平面A1BD.

(方法二)如图,以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,设正方体的棱长为1,则可求得M,N,D(0,0,0),A1(1,0,1),B(1,1,0),于是=(1,0,1),=(1,1,0),

设平面A1BD的法向量是n=(x,y,z),

则n·=0,且n·=0,得

取x=1,得y=-1,z=-1.

∴n=(1,-1,-1).

又·n=·(1,-1,-1)=0,

∴⊥n,且MN⊄平面A1BD.∴MN∥平面A1BD.

(方法三)∵)-)=)=.

∴.

又MN⊄平面A1BD,∴MN∥平面A1BD.

12. 证明(1)∵AB,AD,AP两两垂直,∴建立如图所示的空间直角坐标系.

设PA=AB=BC=1,

则P(0,0,1).

∵∠ABC=60°,∴△ABC为正三角形.

∴C,E,A(0,0,0).设D(0,y,0),=(,0),=(-,y-,0).由AC⊥CD,得=0,即y=,则D,

∴.又,

∴=-=0,

∴,即AE⊥CD.

(2)(方法一)∵=(1,0,0),,

∴设平面ABE的一个法向量为n=(x,y,z),

则

令y=2,则z=-,∴n=(0,2,-).

∵,显然n.

∴∥n,∴⊥平面ABE,即PD⊥平面ABE.

(方法二)∵P(0,0,1),∴.

又×(-1)=0,

∴,即PD⊥AE.

又=(1,0,0),∴=0,

∴PD⊥AB.

又AB∩AE=A,AB⊂平面ABE,AE⊂平面ABE,

∴PD⊥平面ABE.

13.A　c=ma+nb+(4,-4,1)=(m,m,m)+(0,2n,-n)+(4,-4,1)=(m+4,m+2n-4,m-n+1),

由c为平面α的法向量,

得解得

14.D　A,B,C中均能推出l∥α,或l⊂α,但不能确定一定能表示为l∥α.

15.D　∵a·u=-3+4-1=0,∴a⊥u,∴l∥α或l⊂α.

故选D.

16.A　∵n1·=2×1+(-3)×0+1×(-2)=0,n1·=2×1-3×1+1×1=0,

∴n1⊥,n1⊥,AB∩AC=A,

∴n1也为平面ABC的一个法向量.

又平面α与平面ABC不重合,∴平面α与平面ABC平行.

故选A.

17.ABC　对于A,由=2×(-1)+(-1)×2+(-4)×(-1)=0,可得,所以A正确;

对于B,由=(-1)×4+2×2+(-1)×0=0,所以,所以B正确;

对于C,由,可得向量是平面ABCD的一个法向量,所以C正确;

对于D,由是平面ABCD的一个法向量,可得,所以D不正确.

故选ABC.

18.(-6,3,2)(答案不唯一)　∵在长方体ABCD-A1B1C1D1中,AB=4,BC=2,CC1=3,E,F分别是BC,CD的中点,以D为原点,分别以DA,DC,DD1所在直线为坐标轴建立空间直角坐标系,则D1(0,0,3),E(1,4,0),F(0,2,0),=(1,4,-3),=(0,2,-3),设平面D1EF的一个法向量是n=(x,y,z),

则取y=3,得n=(-6,3,2),则平面D1EF的一个法向量是(-6,3,2).

19.(-2,4,1)或(2,-4,-1)　据题意,得=(-1,-1,2),=(1,0,2).

设n=(x,y,z),∵n与平面ABC垂直,

∴可得

∵|n|=,∴,

解得y=4或y=-4.

当y=4时,x=-2,z=1;当y=-4时,x=2,z=-1.

∴n的坐标为(-2,4,1)或(2,-4,-1).

20. (1)证明∵平面CDEF⊥平面ABCD,ED⊥CD,ED⊂平面CDEF,平面CDEF∩平面ABCD=CD,

∴ED⊥平面ABCD,AD⊂平面ABCD,即ED⊥AD.

过F作FG⊥DC于G,过G作GH∥AD交AB于H.

∵四边形CDEF为直角梯形,AB=3EF=3,

∴ED∥FG,即FG⊥AD,则FG⊥HG,且HG=,HB=2,∠GHB=45°,

∴BG2=HG2+HB2-2HG×HBcos∠GHB,得BG2=2,即HG2+BG2=HB2,

∴HG⊥BG,而BG∩FG=G,即HG⊥平面FBG,又BF⊂平面FBG,

∴HG⊥BF,故AD⊥BF.

(2)解以D为原点,平面ABCD上过点D垂直于DC的直线为x轴,DC所在直线为y轴,DE所在直线为z轴,建立空间直角坐标系,如图所示,

∴A(1,-1,0),B(1,2,0),C(0,3,0),E(0,0,a),F(0,1,a),则=(-1,1,a),=(0,-2,a).

设=λ=λ(0,-2,a)=(0,-2λ,aλ)(易知λ≠0),则=(0,3,0)+(0,-2λ,aλ)=(0,3-2λ,aλ),

设平面BDM的法向量为n=(x1,y1,z1),

则

取x1=2,则n=(2,-1,).

若AE∥平面BDM,则·n=(-1,1,a)·(2,-1,)=-2-1+=0,解得λ=,

∴线段CF上存在一点M,满足AE∥平面BDM,此时.