人教版数学 九上 第23章 旋转 单元综合能力测试卷

人教版数学 九上 第23章 《旋转 》单元 单元综合能力测试卷

一．选择题（共30分）

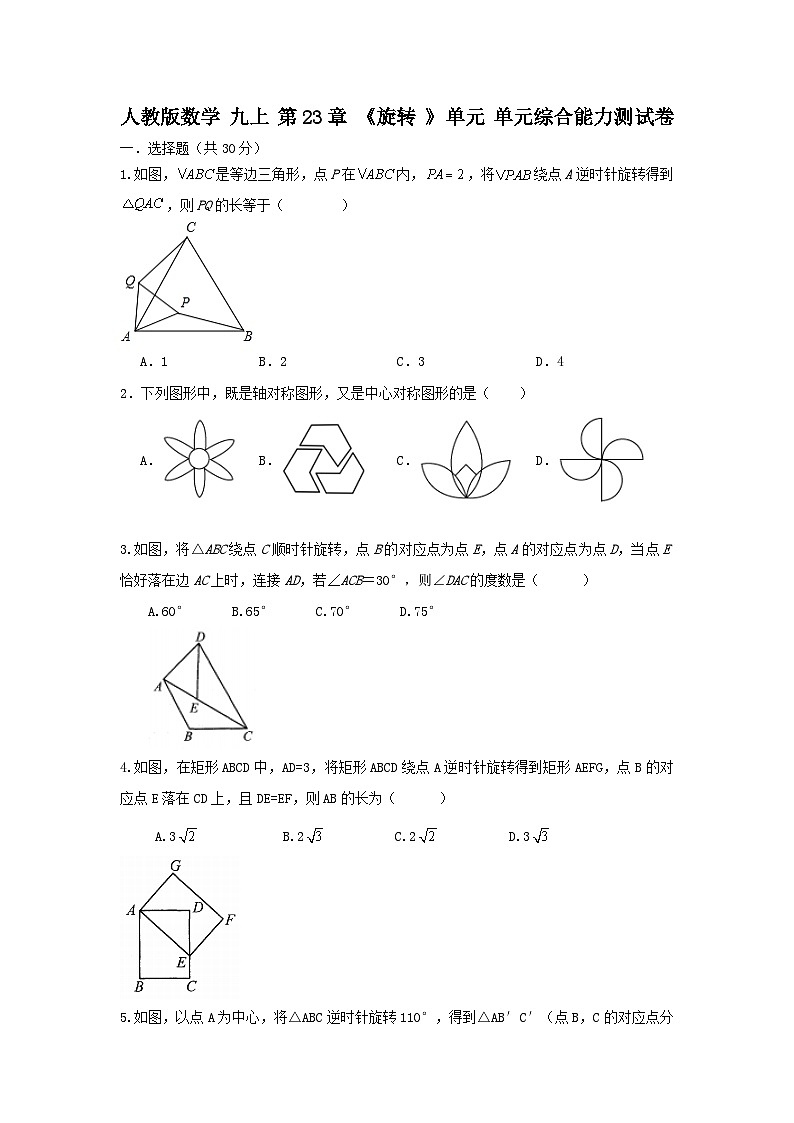
1.如图，是等边三角形，点P在内，，将绕点A逆时针旋转得到，则PQ的长等于（    ）

A．1 B．2 C．3 D．4

2．下列图形中，既是轴对称图形，又是中心对称图形的是（　　）

A． B． C． D．

3.如图，将△ABC绕点C顺时针旋转，点B的对应点为点E，点A的对应点为点D，当点E恰好落在边AC上时，连接AD，若∠ACB＝30°，则∠DAC的度数是（　　　）

A.60°  B.65°  C.70°  D.75°  

4.如图，在矩形ABCD中，AD=3，将矩形ABCD绕点A逆时针旋转得到矩形AEFG，点B的对应点E落在CD上，且DE=EF，则AB的长为（      ）

 A.3            B.2          C.2          D.3

5.如图，以点A为中心，将△ABC逆时针旋转110°，得到△AB′C′（点B，C的对应点分别为点B′，C′），连接BB′，若AC′∥BB′，则∠CAB′的度数为（    ）

A.45°           B.60°           C.70°             D.75°

6.如图，在正方形ABCD中，将边BC绕点B逆时针旋转至BC′，连接CC′，DC′，若∠CC′D=90°，BC′=2，则线段C°D的长度为（     ）

A.              B.2            C.4             D.

7．如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，

∠A′B′C′可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，

点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为（　　）

A．4 B．6 C．3  D．3

8．如图，将矩形 ABCD 绕点 A 顺时针旋转到矩形 AB′C′D′的位置，

旋转角为α(0°＜α＜90°)．若∠1＝112°，则∠α的大小是（　　）

A．68° B．20° C．28° D．22°

9.如图，在中，是斜边上两点，且

将绕点顺时针旋转90°后，得到连接下列结论：

① ②

③的面积等于四边形的面积；

④ ⑤

其中正确的是（　　）

A．①②④ B．③④⑤

C．①③④ D．①③⑤

10.如图，正方形ABCD中，E是AB边上一点，将△CBE绕点C顺时针旋转后，得到△CDF，连接EF交BD于点G，连接CG，过点E作EH⊥BD于点H；下列结论:①＝90°；②∠DCG＝∠BCE；③CG⊥EF；④BC＝GH.其中正确的是（  ）

A.①②③  B.①③④  C.②③④  D.①②④

二．填空题（共24分）

11.点（1，a2）关于原点对称的点在第四象限，则a的取值范围是_________.  

12.如图所示的图案由三个叶片组成，绕点O旋转120°后可以和自身重合，若每个叶片的面积为10cm2，∠AOB＝120°，则图中阴影部分的面积之和为_________cm2.   

13.如图，在四边形ABCD中，∠ABC＝30°，将△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，若AB＝3，BC＝4，则BD＝_________.    

14.如图，△ABC是等腰直角三角形，BC是斜边，现将△ABP绕点A逆时针旋转后能与△ACP′重合，已知AP=4，则PP′长度为          ．

15.如图，在等边△ABC中，D是AC边上一点，连接BD，将△BCD绕点B逆时针旋转60°，

得到△BAE，连接ED，若BC=10，BD=9，则△AED的周长是         ．

16 . 如图，在平面直角坐标系中，

将△ABO绕点A顺指针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去……，

若点A(，0)，B(0，4)，则点B2019的横坐标为            ．

三．解答题（共66分）

17.（6分）作图题：如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；①将向x轴正方向平移5个单位得，

②将再以O为旋转中心，逆时针旋转得，

③将再以O为对称中心，得，

画出平移和旋转及中心对称后的图形．

18.（8分）.如图，点D是等边△ABC内一点，DA＝13，DB＝19，DC＝21，

将△ABD绕点A逆时针旋转到△ACE的位置，求△DEC的周长．

19.（8分）如图，平面直角坐标系中，A（1，），将线段OA绕原点O顺时针旋转120°得到线段.（1）直接写出OA的长为_________；OA与x轴正半轴的夹角为_________°；

（2）求点的坐标.

20.如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D在CA的延长线上，点E在边AB上，且AE＝AD，M为BE的中点.

（1）直接写出的值为_______；

（2）将△ADE绕点A按顺时针旋转到图2的位置，连接AM，CD.试问（1）中的结论还是否成立？说明理由.

21.（10分）如图所示，把一个直角三角尺绕着角的顶点顺时针旋转，

使得点与的延长线上的点重合，已知．

（1）三角尺旋转了多少度？连结，试判断的形状；

（2）求的长；

（3）边结，试猜想线段与的大小关系，并证明你的结论．

22.（12分）如图，四边形ABCD为正方形，E为正方形内一点，∠CEB＝90°.将线段BE绕点B顺时针旋转90°，得到线段BF，连接AF，射线BE与AF交于点M.

（1）直接写出AE与CF的关系；

（2）求证：AM＝MF；

（3）若BF＝3，ME＝1，求线段AF的长.

.

23．（12分）如图，中，，把绕着点逆时针旋转，得到，点在上．

（1）若，求得度数；

（2）若，，求中边上的高．