高中人教B版 (2019)5.4 统计与概率的应用课文内容课件ppt

这是一份高中人教B版 (2019)5.4 统计与概率的应用课文内容课件ppt，共37页。PPT课件主要包含了目录索引等内容，欢迎下载使用。

基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
知识点1　统计的实际应用1.随机抽样有简单随机抽样和分层抽样两种.其共同点是在抽样过程中每个个体被抽到的机会相等,当总体的个体之间差异程度较小和总体中的个体数目较少时,常采用简单随机抽样;当已知总体由差异明显的几部分组成时,常采用分层抽样.2.平均数、中位数、众数、百分位数与方差、标准差都是重要的数字特征,利用它们可对总体进行一种简明的描述,它们所反映的情况有着重要的实际意义,平均数、中位数、众数、百分位数可描述总体的集中趋势,方差和标准差可描述波动大小.
名师点睛在对一些数据进行统计时,要根据数据的特点和统计结果的精确度选择合适的统计图表.如果需要根据图表了解各数据在某区间所占的概率,可以使用柱形图,例如统计一批产品中的优等品所占的频率;如果要了解数据的增减情况,可以采用折线图,例如统计一个人的成绩变化情况;如果要了解数据的全部信息,可使用茎叶图,例如篮球比赛的计分.
过关自诊1.判断正误.(正确的画√,错误的画×)(1)平均数、众数与中位数从不同的角度描述了一组数据的集中趋势.(　　)(2)一组数据的方差越大,说明这组数据越集中.(　　)(3)频率分布直方图中,小矩形的面积越大,表示样本数据落在该区间的频率越大.(　　)
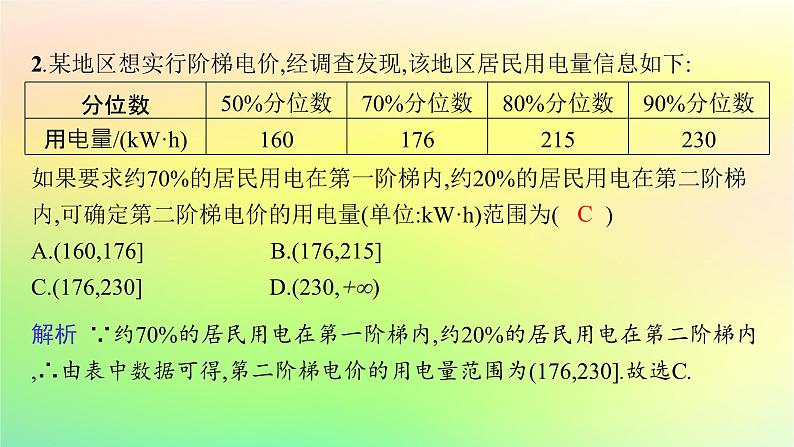
2.某地区想实行阶梯电价,经调查发现,该地区居民用电量信息如下:
如果要求约70%的居民用电在第一阶梯内,约20%的居民用电在第二阶梯内,可确定第二阶梯电价的用电量(单位:kW·h)范围为(　　)　　　　　　　　　　　　　A.(160,176] B.(176,215]C.(176,230]D.(230,+∞)
解析 ∵约70%的居民用电在第一阶梯内,约20%的居民用电在第二阶梯内,∴由表中数据可得,第二阶梯电价的用电量范围为(176,230].故选C.
知识点2　概率的实际应用1.频率是随机的,随着试验的不同而变化;概率是多次试验的频率的稳定值,是一个常数,不要用一次或少数次试验中的频率来估计概率.2.概率是描述随机事件发生可能性大小的度量,它已经渗透到人们的日常生活中,成为一个常用的词汇,任何事件的概率是[0,1]内的一个数,它度量该事件发生的可能性.小概率事件(概率接近0)很少发生,而大概率事件(概率接近1)则经常发生.
名师点睛1.古典概型概率的计算关键要分清样本点的总数n与事件A包含的样本点的个数m,再利用公式P(A)= 求解.有时需要用列举法把样本点一一列举出来,在列举时必须按某一顺序做到不重不漏.2.解决概率问题的注意点(1)概率与频率的关系;(2)互斥事件与对立事件概率公式的应用;(3)掌握古典概型的概率公式P= (n为样本点的总数,m为所求事件包含的样本点个数);(4)对于较复杂的古典概型的概率可借助于互斥事件或对立事件去求.
3.利用独立性解决复杂古典概型问题对于一些较为复杂的古典概型问题,可以直接根据古典概型的概率计算公式求解,但这时样本空间中样本点较多,计算复杂.因此也可将问题转化,将事件分解为相互独立事件,然后根据相互独立事件同时发生的概率公式求解,这样可以简化计算过程.
过关自诊1.[2023广东高一课时练习]从一群玩游戏的小孩中抽出k人,一人分一个苹果,让他们返回继续玩游戏,一会儿后,再从中任取m人,发现其中有n个小孩曾分过苹果,估计小孩的人数为(　　)
2.某商店试销某种商品20天,获得如下数据:
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率.则当天商店不进货的概率为　　　　. 
解析 记“当天商品销售量为0件”为事件A,“当天商品销售量为1件”为事件 B,“当天商店不进货”为事件C,则
探究点一　用样本的分布估计总体分布
【例1】 某学校兴趣小组为了了解移动支付在大众中的熟知度,对15~65岁的人群随机抽样调查,调查的问题是:“你会使用移动支付吗?”其中,回答“会”的共有n人.把这n人按照年龄分成5组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65].然后绘制成如图所示的频率分布直方图.其中,第1组的频数为20.
(1)求n和x的值;(2)从第1,3,4组中用分层抽样的方法抽取6人,求从第1,3,4组分别抽取的人数;(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
解 (1)由题意可知,由10×(0.020+0.036+x+0.010+0.004 )=1,解得x=0.030.
(3)设第1组抽取的2人为A1,A2,第3组抽取的3人为B1,B2,B3,第4组抽取的1人为C.则从这6人中随机抽取2人的样本空间Ω={(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C),(A2,B1),(A2,B2),(A2,B3),(A2,C),(B1,B2),(B1,B3),(B1,C),(B2,B3),(B2,C),(B3,C)},共有15个样本点.记A:“抽取的2人来自同一个组”,则A={(A1,A2),(B1,B2),(B1,B3),(B2,B3)},共4个样本点.所以抽取的2人来自同一个组的概率P(A)= .
规律方法　总体分布中相应的统计图表主要包括:频率分布直方图、频率分布折线图等.通过这些统计图表给出的相应统计信息可以估计总体的相关信息.
变式训练1某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:m3),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3 m3的人数,说明理由;(3)估计居民月均用水量的中位数.
解 (1)由频率分布直方图可知,月均用水量在[0,0.5)的频率为0.08×0.5=0.04.同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.(2)由(1)知,该市100位居民中月均用水量不低于3 m3的频率为0.06+0.04+0.02=0.12.由以上样本的频率分布,可以估计30万居民中月均用水量不低于3 m3的人数为300 000×0.12=36 000.
(3)设中位数为x.因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.由0.50×(x-2)=0.5-0.48,解得x=2.04.故可估计居民月均用水量的中位数为2.04.
探究点二　概率在整体估计中的应用
【例2】 某家具厂为某游泳比赛场馆生产观众座椅.质检人员对该厂所产2 500套座椅进行抽检,共抽检了100套,发现有5套次品.该厂所产2 500套座椅中大约有多少套次品?
解 设有n套次品,则 ,解得n=125.所以该厂所产2 500套座椅中大约有125套次品.
规律方法　用古典概型概率的观点求随机事件的概率时,首先对于在试验中出现的结果的可能性认为是相等的,其次是通过一个比值的计算来确定随机事件的概率.
变式训练2某校为调查期末考试中高一学生作弊情况,随机抽取了200名高一学生进行调查,设计了两个问题,问题1:你出生月份是奇数吗?问题2:期末考试中你作弊了吗?然后让受调查的学生每人掷一次币,出现“正面朝上”则回答问题1,出现“反面朝上”则回答问题2,答案只能填“是”或“否”,不能弃权.结果统计后得到了53个“是”的答案,则估计有百分之几的学生作弊了?
解 由于硬币正面朝上,反面朝上的概率一样,即有100人回答问题1,100人回答问题2.由于问题1答案为“是”的概率为 ,有100× =50(人).则53个“是”中应该有3个“是”回答问题2,从而作弊学生大约占3%.
探究点三　概率在决策中的应用
【例3】 如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
(1)试估计40分钟内不能赶到火车站的概率;(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;(3)现甲、乙两人分别有40分钟和50分钟的时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
解 (1)因为一共抽取了100人进行调查,其中40分钟内不能赶到火车站的有12+12+16+4=44人,用频率估计概率,可得所求概率为 =0.44.(2)选择L1的有60人,选择L2的有40人,故由调查结果得所求各频率为
(3)记事件A1,A2分别表示甲选择路径L1和L2时,在40分钟内赶到火车站;记事件B1,B2分别表示乙选择路径L1和L2时,在50分钟内赶到火车站.由(2)知,P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,P(A1)>P(A2),∴甲应选择路径L1.P(B1)=0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4=0.9,P(B2)>P(B1),∴乙应选择路径L2.
变式训练3某厂家声称自己的产品合格率为99%,市场质量管理人员抽取了这个厂家的2件产品进行检验,发现2件都不合格,厂家所声称的合格率可信吗?
解 不可信.如果该厂产品的合格率为99%,则随机抽取一件产品,不合格的概率为1-99%=1%.此时,随机抽取2件,都不合格的概率为1%×1%=0.000 1,也就是说,如果厂家所称的合格率可信,那么就发生了一件可能性只有0.01%的事.但是一件概率只有0.01%的事是不太可能发生的,因此有理由怀疑厂家所声称的合格率是不可信的.
1.某养鸡厂用鸡蛋孵化小鸡,用200个鸡蛋孵化出170只小鸡,由此估计,要孵化出2 500只小鸡,大约需要鸡蛋的个数为(　　)A.3 022B.2 941C.2 800D.3 125
2.如图所示,茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为(　　)
3.甲、乙两人投篮命中率分别为 ,则甲、乙两人各投一次,恰好命中一次的概率为　　　　. 
4.某公司有5万元资金用于投资开发项目,如果成功,一年后可获收益12%;如果失败,一年后将丧失全部资金的50%.下表是去年200例类似项目开发的实施结果.
试估计该公司一年后可获收益为　　　元.