新教材2023_2024学年高中数学第4章概率与统计本章总结提升课件新人教B版选择性必修第二册

这是一份新教材2023_2024学年高中数学第4章概率与统计本章总结提升课件新人教B版选择性必修第二册，共46页。

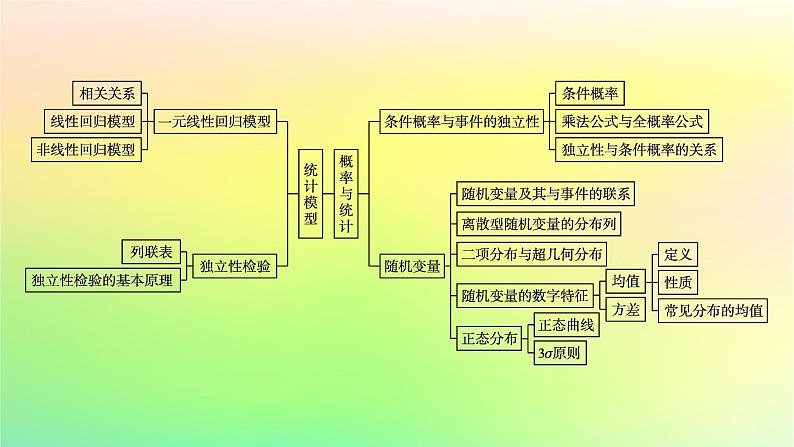
第四章本章总结提升知识网络·整合构建专题突破·素养提升目录索引 知识网络·整合构建专题突破·素养提升专题一　条件概率与全概率公式1.求条件概率及运用全概率公式求概率问题的关键是能区分P(A),P(B|A)以及P(AB)在题目情境下的含义,并明确三者之间的关系,完成转化.2.掌握条件概率与全概率公式,重点提升逻辑推理和数学运算的核心素养.【例1】 某班有6名班干部,其中男生4人,女生2人,任选3人参加学校的义务劳动.(1)求男生甲或女生乙被选中的概率;(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(A)和P(B|A).规律方法　条件概率的两个求解策略(2)缩小样本空间法(直接法):利用 求解,常用于古典概型的概率计算问题.变式训练1(多选题)[2023广东东莞高二期末]有甲、乙两台车床加工同一型号的零件,甲车床加工的优质品率为90%,乙车床加工的优质品率为80%,加工出来的零件混放在一起.已知甲、乙两台车床加工的零件数分别占总数的60%,40%.任取一个零件,用事件A1,A2分别表示取到的零件来自甲、乙车床,事件B表示取到的零件为优质品,则下列选项正确的有(　　)A.P(A1B)=0.54 B.P(B|A1)=0.9C.P(B|A2)=0.32 D.P(B)=0.86ABD解析 依题意得:用事件A1表示取到的零件来自甲车床,则P(A1)=0.6,用事件A2表示取到的零件来自乙车床,则P(A2)=0.4,所以P(B|A1)=0.9,P(B|A2)=0.8,B正确,C错误;对于A,P(B|A1)=解得P(A1B)=0.54,A正确;对于D,由全概率公式得P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)=0.6×0.9+0.4×0.8=0.86,D正确.故选ABD.专题二　相互独立事件的概率与二项分布1.利用独立事件概率公式求概率问题通常先转化成互斥事件的概率的和,要注意二项分布这一特殊的独立事件概率模型.2.掌握独立事件概率公式,重点提升逻辑推理和数学运算的核心素养.【例2】 计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书,甲、乙、丙三人在理论考试中“合格”的概率依次为 ,在实际操作考试中“合格”的概率依次为 ,所有考试是否合格相互之间没有影响.(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.解 (1)设“甲获得合格证书”为事件A,“乙获得合格证书”为事件B,“丙获得合格证书”为事件C,则由题得,因为P(C)>P(B)>P(A),所以丙获得合格证书的可能性最大.(2)设“三人考试后恰有两人获得合格证书”为事件D,则规律方法　求相互独立事件同时发生的概率需注意的三个问题(1)“P(AB)=P(A)P(B)”是判断事件是否相互独立的充要条件,也是解答相互独立事件概率问题的重要工具.(2)涉及“至多”“至少”“恰有”等字眼的概率问题,务必分清事件间的相互关系.(3)公式“P(A+B)=1-P( )”常应用于求相互独立事件至少有一个发生的概率.变式训练2[人教A版教材习题]已知每门大炮击中目标的概率都是0.3,现在n门大炮同时对某一目标各射击一次.(1)当n=10时,求恰好击中目标3次的概率(精确到0.001).(2)如果使目标至少被击中一次的概率超过95%,至少需要多少门大炮?解 设击中目标的门数为X,由题意知X~B(10,0.3).(1)P(X=3)= ×0.33×0.77≈0.267.(2)目标至少被击中一次的概率为P(X≥1)=1-P(X=0)=1-0.7n.欲使1-0.7n≥0.95,即0.7n≤0.05,解得n≥9.因此,目标至少被击中一次的概率超过95%,至少需要9门大炮.专题三　离散型随机变量的分布列、均值和方差1.均值和方差是随机变量重要的数字特征,要掌握求解的步骤,并明确其现实意义,利用均值和方差进行决策是近年考试的热点.2.掌握均值和方差的计算,重点提升逻辑推理和数据分析的核心素养.【例3】 一次同时投掷两枚相同的正方体骰子(骰子质地均匀,且各面分别刻有1,2,2,3,3,3六个数字),(1)设随机变量η表示一次掷得的点数和,求η的分布列;(2)若连续投掷10次,设随机变量ξ表示一次掷得的点数和大于5的次数,求E(ξ),D(ξ).解 (1)由已知,随机变量η可能的取值为2,3,4,5,6.设掷一次正方体骰子所得点数为η0,所以η的分布列为 规律方法　求离散型随机变量ξ的期望与方差的步骤 变式训练3某公司有日生产件数为95的“生产能手”3人,有日生产件数为55的“菜鸟”2人,从这5人中任意抽取2人,则2人的日生产件数之和X的方差为　　　　. 576 专题四　正态分布的概率1.正态分布常常与统计、相互独立事件等相结合进行考查.2.掌握正态分布,重点提升数学运算和数据分析的核心素养.【例4】 为加强对企业产品质量的管理,市监局到区机械厂抽查机器零件的质量,共抽取了600件螺帽,将它们的直径和螺纹距之比Z作为一项质量指标,由测量结果得如下频率分布直方图:(1)求这600件螺帽质量指标值的样本平均数 ,样本方差s2(在同一组数据中,用该组区间的中点值作代表).(2)由频率分布直方图可以近似地认为,这种螺帽的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数 ,σ2近似为样本方差s2.①利用该正态分布,求P(185.03≤Z≤229.94);②现从该企业购买了100件这种螺帽,记X表示这100件螺帽中质量指标值位于区间[185.03,229.94]的件数,利用①的结果,求E(X).附: ≈14.97.若Z~N(μ,σ2),则P(μ-σ≤Z≤μ+σ)≈0.683,P(μ-2σ≤Z≤μ+2σ)≈0.954, P(μ-3σ≤Z≤μ+3σ)≈0.997.解 (1)抽取的螺帽质量指标值的样本平均数 和样本方差s2分别为 =170×0.05+180×0.12+190×0.18+200×0.30+210×0.19+220×0.10+230×0.06=200,s2=(-30)2×0.05+(-20)2×0.12+(-10)2×0.18+0×0.30+102×0.19+ 202×0.10+302×0.06=224.(2)①由(1)知,Z~N(200,224),从而P(200-14.97≤Z≤200+14.97)=2P(185.03≤Z≤200)≈0.683,P(200-29.94≤Z≤200+29.94)=2P(200≤Z≤229.94)≈0.954,P(185.03≤Z≤229.94)=P(185.03≤Z≤200)+P(200≤Z≤229.94)=0.818 5.②由①知,一件螺帽的质量指标值位于区间[185.03,229.94]的概率为0.818 5,依题意知X~B(100,0.818 5),所以E(X)=100×0.818 5=81.85.规律方法　正态分布的概率求法(1)注意“3σ”原则,记住随机变量在三个区间内取值的概率.(2)注意数形结合.由于正态分布密度曲线具有完美的对称性,可充分体现数形结合的思想,因此运用对称性结合图象解决某一区间内的概率问题成为热点问题.变式训练4为了解某地区高三男生的身体发育状况,抽查了该地区1 000名年龄在17.5岁至19岁的高三男生的体重情况,抽查结果表明他们的体重X(单位:kg)服从正态分布N(μ,22),且正态分布密度曲线如图所示.若体重大于等于58.5 kg小于等于62.5 kg属于正常情况,则这1 000名男生中属于正常情况的人数是(　　)A.997 B.954 C.819 D.683 D 解析 由题可知μ=60.5,σ=2,故P(58.5≤X≤62.5)=P(μ-σ≤X≤μ+σ)≈68.3%,从而这1 000名男生中属于正常情况的人数是1 000×68.3%=683.专题五　一元线性回归模型及其应用1.回归分析是将两个变量拟合成一个函数模型,如果拟合成一次函数模型需通过散点图和相关系数判断拟合的合理性,对于非线性模型要转化成线性模型.2.主要培养数学建模和数据分析的数学核心素养.【例5】 以下是某地收集到的新房屋的销售价格y和房屋的面积x的数据: (1)画出数据对应的散点图;(2)若x与y线性相关,求回归直线方程;(3)根据(2)的结果估计当房屋面积为150 m2时的销售价格.解 (1)数据对应的散点图如图所示. (3)根据(2),当x=150时,销售价格的估计值为 =0.196 2×150+1.814 2 =31.244 2(万元).规律方法　若在散点图中样本点大致分布在一条直线附近,则利用线性变式训练5为缓解某种疾病造成的医疗压力,某市医疗器械公司转型升级,从9月1日开始投入呼吸机生产,该公司9月1目~9月9日连续9天的呼吸机日生产量为yi(单位:百台,i=1,2,…,9),数据作了初步处理,得到如图所示的散点图.(1)从9个样本点中任意选取2个,在2个样本点的生产量都不高于300台的条件下,求2个样本点都高于200台的概率;(2)由散点图分析,样本点都集中在曲线y=ln(bt+a)的附近,求y关于t的回归直线方程y=ln(bt+a),并估计该公司从生产之日起,需要多少天呼吸机日生产量可超过500台.参考数据:e5≈148.4. 解 (1)由散点图知,不高于300台的点有5个,其中高于200台的点有4个,则在2个样本点的生产量都不高于300台的条件下,2个样本点都高于200台的概率为(2)y=ln(bt+a)⇔z=ey=bt+a,则由回归方程系数求解公式知,故y=ln(4t-1),y=ln(4t-1)>5⇒4t-1>e5≈148.4⇒t>37.35.需要38天呼吸机日生产量可超过500台.专题六　独立性检验1.首先要明确独立性检验的适用情境,列出2×2列联表计算χ2后,分析判断相关性结论的可信程度.2.掌握独立性检验,提升数学运算、数据分析的数学核心素养.【例6】 某公司为了解服务质量,随机调查了100位男性顾客和100位女性顾客,每位顾客对该公司的服务质量进行打分.已知这200位顾客所打分数均在[25,100]之间,根据这些数据得到如下的频数分布表:(1)求这200位顾客所打分数的平均值(同一组数据用该组区间的中点值为代表);(2)若顾客所打分数不低于70分,则该顾客对公司服务质量的态度为满意;若顾客所打分数低于70分,则该顾客对公司服务质量的态度为不满意,根据所给数据,完成下列2×2列联表,并根据列联表,判断是否有99%的把握认为顾客对该公司服务质量的态度与性别有关?(2)根据所给数据,可得如下2×2列联表: 因为9.524>6.635,所以有99%的把握认为顾客对该公司服务质量的态度与性别有关.规律方法　独立性检验的一般步骤(1)根据样本数据制成2×2列联表;(2)根据公式计算χ2;(3)比较χ2与临界值的大小关系并作统计推断.变式训练6某班主任对全班30名男生进行了作业量多少的调查,数据如下表:该班主任据此推断男生认为作业多与喜欢玩电脑游戏有关系,则这种推断犯错误的概率不超过　　　　　. 5%