奥数六年级下册秋季课程第8讲《面积计算》课件+教案

展开

这是一份奥数六年级下册秋季课程第8讲《面积计算》课件+教案，文件包含奥数六年级下册秋季课程第8讲《面积计算》课件pptx、奥数六年级下册秋季课程第8讲《面积计算》教案doc等2份课件配套教学资源，其中PPT共18页，欢迎下载使用。

奥数六年级下册秋季课程
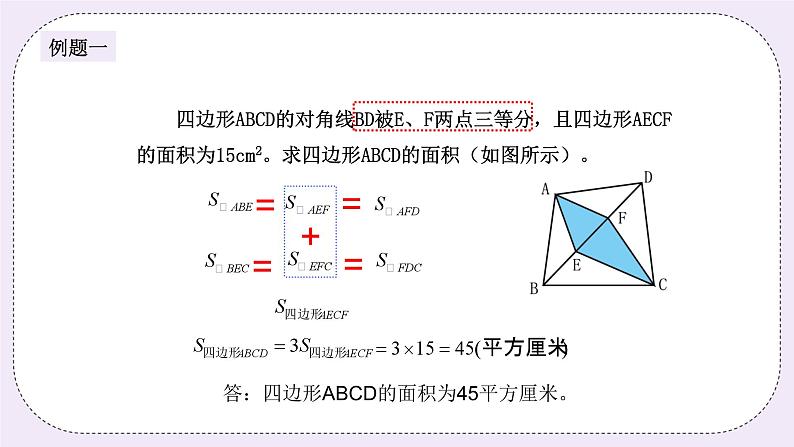
四边形ABCD的对角线BD被E、F两点三等分，且四边形AECF的面积为15cm2。求四边形ABCD的面积（如图所示）。
答：四边形ABCD的面积为45平方厘米。
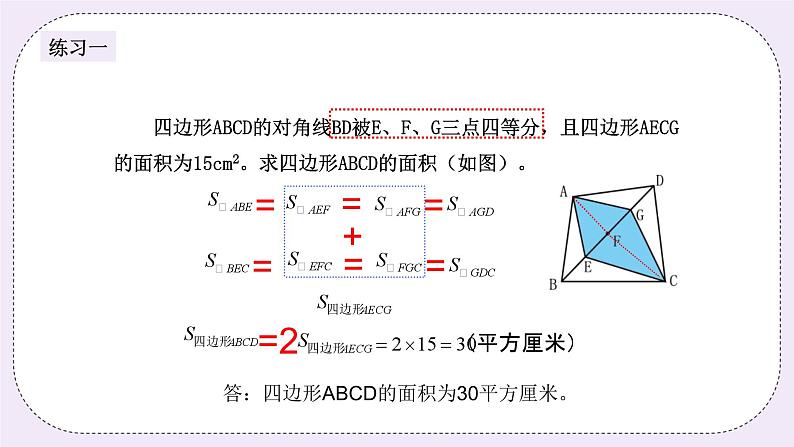
四边形ABCD的对角线BD被E、F、G三点四等分，且四边形AECG的面积为15cm2。求四边形ABCD的面积（如图）。
答：四边形ABCD的面积为30平方厘米。
5、4、3、2、1（猜一数学名词）
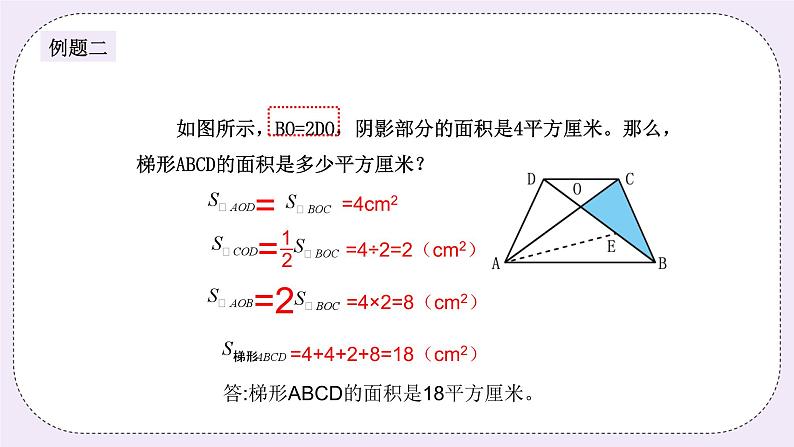
如图所示，BO=2DO，阴影部分的面积是4平方厘米。那么，梯形ABCD的面积是多少平方厘米？
=4÷2=2（cm2）
=4×2=8（cm2）
=4+4+2+8=18（cm2）
答:梯形ABCD的面积是18平方厘米。
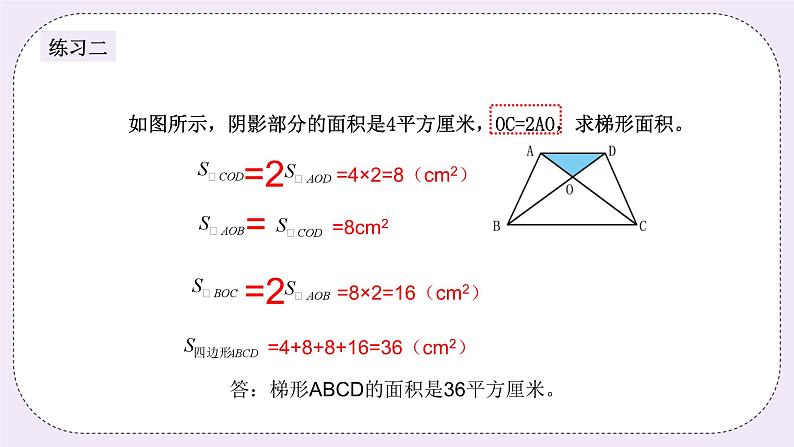
如图所示，阴影部分的面积是4平方厘米，OC=2AO，求梯形面积。
=8×2=16（cm2）
=4+8+8+16=36（cm2）
答：梯形ABCD的面积是36平方厘米。
1. 如果两个三角形是等底等高三角形，则它们的面积相等。2. 如果两个三角形的高相等，则它们的面积比等于对应底之比。
已知图中，三角形ABC的面积为8cm2。AE=ED，BD=2DC，求阴影部分面积。
答：阴影部分的面积为3.2平方厘米。
如图所示，AE=ED，BC=3BD，S△ABC=30cm2。求阴影部分的面积。
答：阴影部分的面积为12平方厘米。
24点游戏！不能移动数字
2 3 3 8
(2×3-3)×8=24
如图所示，长方形ADEF的面积是16平方米，三角形ADB的面积是3平方米，三角形ACF的面积是4平方米，求三角形ABC的面积。
=16÷2=8（m2）
△ACE与△ACF的高
△ABE与△CBE的底
=5÷2=2.5（m2）
=16-3-4-2.5=6.5（m2）
答：三角形ABC的面积是6.5平方米。
如图所示，长方形ABCD的面积是20平方厘米，三角形ADF的面积为5平方厘米，三角形ABE的面积为7平方厘米，求三角形AEF的面积。
=20÷2=10（cm2）
=10-7=3（cm2）
=10-5=5（cm2）
△ADF与△ACF的高
△AEC与△FEC的底
=3÷2=1.5（cm2）
=20-7-5-1.5=6.5（cm2）
答：三角形AEF的面积是6.5平方厘米。
如图所示，如三角形ABC中，三角形BDE、DCE、ACD的面积分别是90,30,28cm2。那么三角形ADE的面积是多少？
两个三角形的高相等，对应的底边之比等于面积之比
△ADC与△BDC的高
=S△ADC:S△BDC
=28:（90+30）
△ADE与△BDE的高
S△ADE:S△BDE
答：三角形ADE的面积是21平方厘米。
如图所示，在三角形ADE中，三角形ABC、BCE、CDE的面积分别是50,24,37cm2。求三角形BDC的面积。
△ACE与△CDE的高
=S△CDE:S△ACE
=37:（50+24）
△BDC和△ABC的高
S△BDC:S△ABC
答：三角形BDC的面积是25平方厘米。
1. 当两个三角形的高相等时，则两个三角形的面积比等于它们对应底之比。2. 在求阴影部分的面积时，有时我们会采用移补的方法，将所求的阴影部分转化成容易求的图形。