江苏省苏州市西安交通大学苏州附属中学2022—2023学年上学期10月八年级数学月考试题

2022-2023学年第一学期阶段随堂练习试卷

               初二年级 数学学科      2022年10月

一．选择题（本大题共10小题，每小题3分，共30分）

1．2022年北京冬奥会会徽“冬梦”以汉字“冬”为灵感来源，运用中国书法的艺术形态，将厚重的东方文化底蕴与国际化的现代风格融为一体．以下是参选的会徽设计的一部分图形，其中是轴对称图形的是（　　）

A．      B．     C．      D．

2．已知△ABC的三条边分别是a、b、c，则下列条件中不能判断△ABC是直角三角形的是（　　）

A．a：b：c＝3：4：5 B．∠C＝∠A+∠B 

C．∠A：∠B：∠C＝1：5：6 D．∠A：∠B：∠C＝3：4：5

3．下列四组数中，是勾股数的是（　　）

A．6，8，10B．0.3，0.4，0.5C．，，D．32，42，52

4．到△ABC的三边距离相等的点是△ABC的（　　）

A．三边中线的交点 B．三条角平分线的交点 

C．三边上高的交点 D．三边垂直平分线的交点

5．在直角三角形中，两条直角边长分别为5，12，则斜边上的中线长为（　　）

A．13 B．12 C．6.5 D．6

6．如图，在△ABC中，AB＝AC，点D为AB边上一点，且AD＝CD＝BC，则∠A的度数为（　　）

A．38° B．36° C．32° D．30°

第6题                                 第7题

7．如图，一架梯子AB长为5米，顶端A靠在墙AC上，这时梯子下端B与墙底端C的距离是3米，梯子下滑后停在DE的位置上，这时测得BE为1米，则梯子顶端A下滑了（　　）

A．1米 B．1.5米 C．2米 D．2.5米

8．如图，将长方形ABCD沿对角线BD折叠，使点C落在点C′处，BC′交AD于E，AD＝8，AB＝4，则重叠部分（即△BDE）的面积为（　　）

A．6 B．7.5 C．10 D．20

9．如图，在△ABC中，AC＝4，∠ACB＝90°，AM=1，CD平分∠ACB交AB于点D，点P是CD上一动点，则PM+PA的最小值为（　　）

A．3 B．4 C．5 D．6

第8题                          第9题                           第10题

10．如图，阴影部分表示以Rt△ABC的各边为直径的三个半圆所组成的两个新月形，面积分别记作S1和S2．若S1+S2＝7，AB＝6，则△ABC的周长是（　　）

A．12.5 B．13 C．14 D．15

二、填空题（本大题共8小题，每小题2分，共16分）

11．在△ABC中，∠A＝100°，当∠B＝　   　°时，△ABC是等腰三角形．

12．已知△ABC中，AB＝6cm，BC＝8cm，AC＝10cm，则△ABC的面积是 　   　cm2．

13．等腰三角形的周长为20cm，一边长为6cm，则底边长为　   　cm．

14．如图，在△ABC中，边AB的垂直平分线OM与边AC的垂直平分线ON交于点O，这两条垂直平分线分别交BC于点 D、E．已知△ADE的周长为13cm．分别连接OA、OB、OC，若△OBC的周长为27cm，则OA的长为 　   　cm．

第14题                                  第15题

15．如图，网格中的每个小正方形的边长为1，A，B是格点（各小正方形的顶点是格点），则以A，B，C为等腰三角形顶点的所有格点C的位置有 　   　个．

16．如图，已知等边△ABC的边长是6，点D在AC上，且CD＝4．延长BC到E，使CE＝CD，连接DE．点F，G分别是AB，DE的中点，连接FG，则FG的长为　   　．

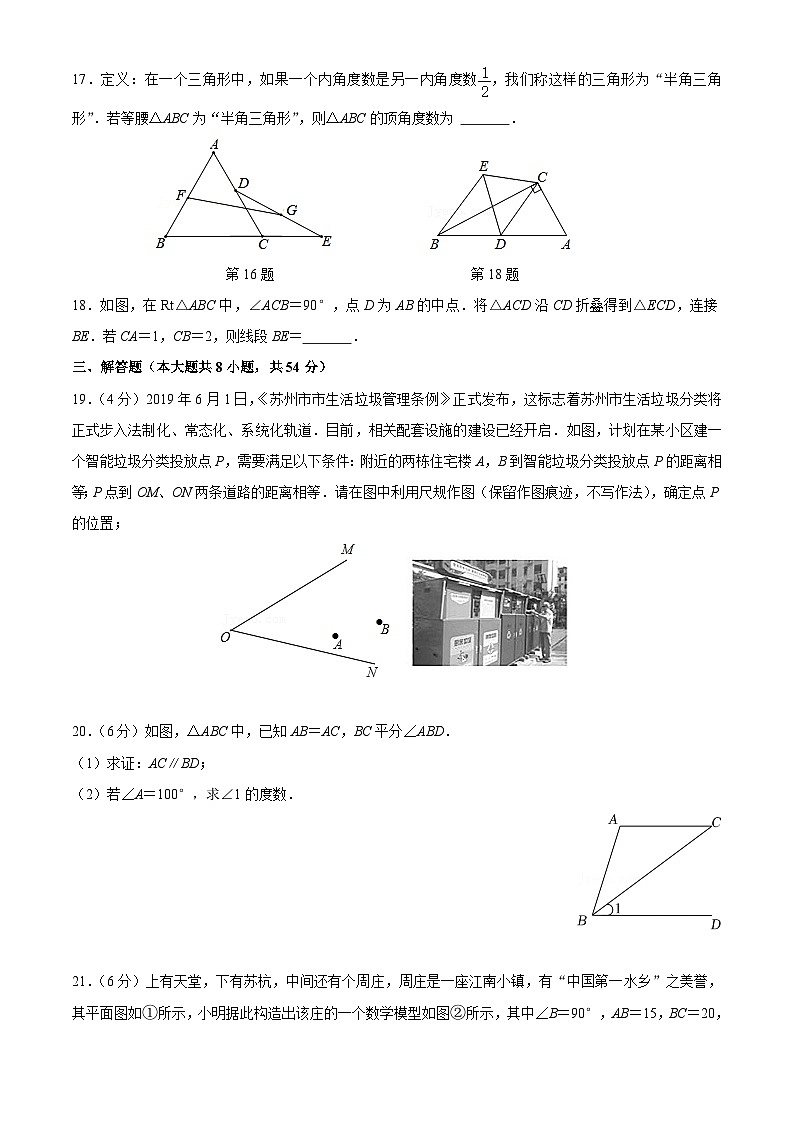
17．定义：在一个三角形中，如果一个内角度数是另一内角度数，我们称这样的三角形为“半角三角形”．若等腰△ABC为“半角三角形”，则△ABC的顶角度数为 　   　．

第16题                            第18题

18．如图，在Rt△ABC中，∠ACB＝90°，点D为AB的中点．将△ACD沿CD折叠得到△ECD，连接BE．若CA＝1，CB＝2，则线段BE＝　   　．

三、解答题（本大题共8小题，共54分）

19．（4分）2019年6月1日，《苏州市市生活垃圾管理条例》正式发布，这标志着苏州市生活垃圾分类将正式步入法制化、常态化、系统化轨道．目前，相关配套设施的建设已经开启．如图，计划在某小区建一个智能垃圾分类投放点P，需要满足以下条件：附近的两栋住宅楼A，B到智能垃圾分类投放点P的距离相等；P点到OM、ON两条道路的距离相等．请在图中利用尺规作图（保留作图痕迹，不写作法），确定点P的位置；

20．（6分）如图，△ABC中，已知AB＝AC，BC平分∠ABD．

（1）求证：AC∥BD；

（2）若∠A＝100°，求∠1的度数．

21．（6分）上有天堂，下有苏杭，中间还有个周庄，周庄是一座江南小镇，有“中国第一水乡”之美誉，其平面图如①所示，小明据此构造出该庄的一个数学模型如图②所示，其中∠B＝90°，AB＝15，BC＝20，CD＝7，AD＝24，求该庄的面积．

22．（6分）如图，CD是∠ACE的平分线．DP垂直平分AB于点P，DF⊥AC于点F，DE⊥BC于点E．

（1）求证：AF＝BE；

（2）若BC＝3cm，AC＝5cm，则CE＝　   　．

23（6分）．如图，点C为线段AB上任意一点（不与点A、B重合），分别以AC、BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE，CA＝CD，CB＝CE，∠ACD与∠BCE都是锐角，且∠ACD＝∠BCE，连接AE交CD于点M，连接BD交CE于点N，AE与BD相交于点P，连接PC．求证：

（1）△ACE≌△DCB；

（2）∠APC＝∠BPC．

24．（8分）用四个全等的直角三角形拼成如图①所示的大正方形，中间也是一个正方形．它是美丽的弦图．其中四个直角三角形的直角边长分别为a，b（a＜b），斜边长为c．

（1）结合图①，求证：a2+b2＝c2；

（2）如图②，将这四个全等的直角三角形无缝隙无重叠地拼接在一起，得到图形ABCDEFGH．若该图形的周长为48，OH＝6．求该图形的面积；

（3）如图③，将八个全等的直角三角形紧密地拼接成正方形PQMN，记正方形PQMN、正方形ABCD、正方形EFGH的面积分别为S1、S2、S3，若S1+S2+S3＝24，则S2＝　   　．

25．（8分）【问题情境】

课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．

小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE＝AD，连接BE．请根据小明的方法思考：

（1）由已知和作图能得到△ADC≌△EDB，依据是　   　．

A．SSSB．SASC．AASD．HL

（2）由“三角形的三边关系”可求得AD的取值范围是　   　．

解后反思：题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．

【初步运用】

如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF．若EF＝3，EC＝2，求线段BF的长．

【灵活运用】

如图3，在△ABC中，∠A＝90°，D为BC中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF，试猜想线段BE、CF、EF三者之间的等量关系，并证明你的结论．

26．（10分）【材料】在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.

根据材料，解决下列问题:

如图，在Rt△ABC中，∠C = 90°，∠A = 30°，BC = 12 cm.动点P从点A出发，沿射线AB运动，动点Q从点B出发，沿射线BC运动，如果动点P以2cm/s，Q以1cm/s的速度同时出发，设运动时间为t（s），解答下列问题:

（1）当t = 2时，BP = _______ ；

（2）t为多少时，△PBQ是等腰三角形?请说明理由.

（3）P、 Q 在运动过程中，△PBQ 的形状不断发生变化，当t为多少时，△PBQ 是直角三角形? 请说明理由.

（4）取AC中点D，连接CP，DP，问CP + DP的最小值等于_________ .