

期中测试卷2023-2024学年人教版数学八年级上册
展开
这是一份期中测试卷2023-2024学年人教版数学八年级上册,共14页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。
八年级上册数学期中综合测试卷
一、单项选择题(每小题2分, 共12分)
1.下列银行标志中,不是轴对称图形的为( )
A. B. C. D.
2.点(﹣2,3)关于y轴的对称点的坐标为( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(2,﹣3)
3.已知等腰三角形的一个内角为40°,则这个等腰三角形的底角为( )
A.40° B.100° C.40°或100° D.40°或70°
4.如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )
A.74° B.38° C.94° D.68°
(第4题图) (第5题图) (第6题图)
5.如图,在△ABC中,AB=AC,分别以点A、点B为圆心,以大于12AB长为半径画弧,两弧交点的连线交AC于点D,交AB于点E,连接BD,若∠A=40°,则∠DBC=( )
A.40° B.30° C.20° D.10°
6.小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.280° B.290° C.285° D.295°
二、填空题(每小题3分, 共24分)
7.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于12BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB= .
8.等腰三角形的周长为20cm,一边长为6cm,则底边长为 cm.
9.若点P(﹣3,4)和点Q(a,b)关于x轴对称,则2a+b= .
10.如图,∠ADB=90°,∠DAB=∠BAC,BD=4,AC=10,则△ABC的面积是 .
(第7题图) (第10题图) (第11题图)
11.如图,AB∥CF,E为DF的中点,若AB=7cm,CF=5cm,则BD= cm.
12.如图,△ABC中AB=AC,AB的垂直平分线交AC于点D.若∠A=40°,则∠DBC= .
(第12题图) (第13题图) (第14题图)
13.如图,把一张长方形纸片ABCD沿EF折叠,∠1=55°,则∠2= 度.
14.如图,已知△ABC中∠A=43°,∠B=73°,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E= 度.
三、解答题(每小题5分,共20分)
15.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.
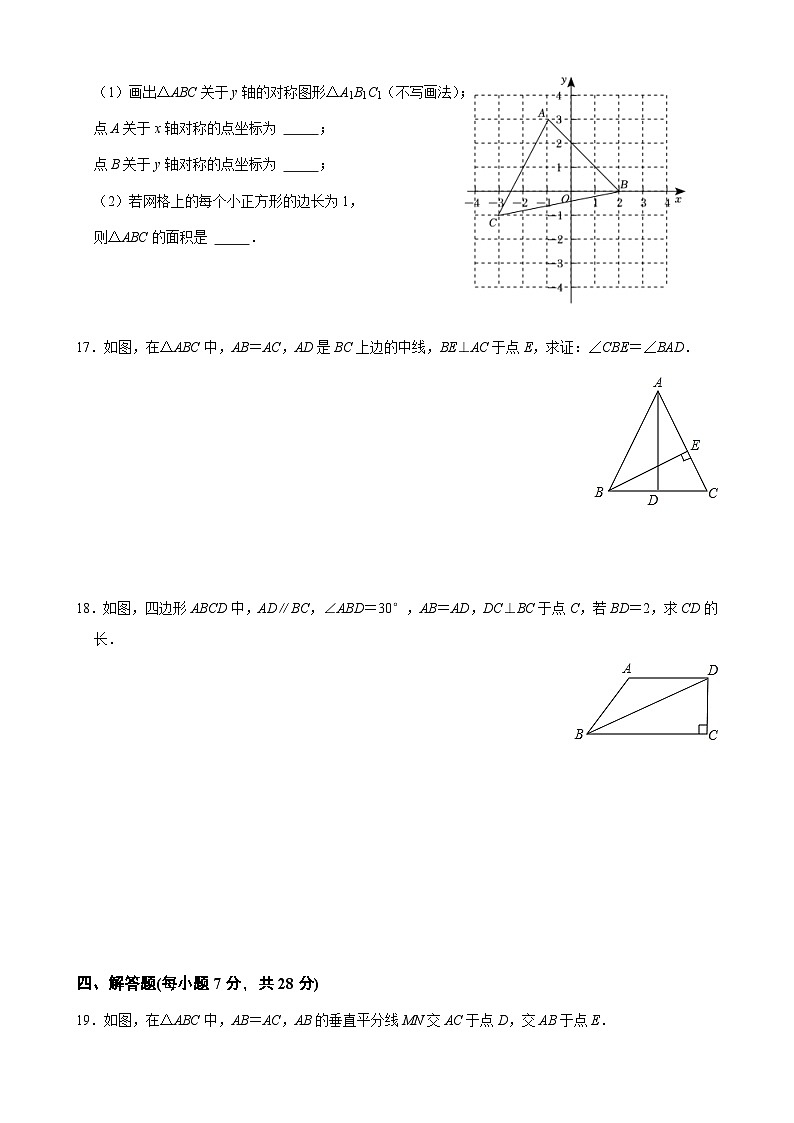
16.如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为 ;
点B关于y轴对称的点坐标为 ;
(2)若网格上的每个小正方形的边长为1,
则△ABC的面积是 .
17.如图,在△ABC中,AB=AC,AD是BC上边的中线,BE⊥AC于点E,求证:∠CBE=∠BAD.
18.如图,四边形ABCD中,AD∥BC,∠ABD=30°,AB=AD,DC⊥BC于点C,若BD=2,求CD的长.
四、解答题(每小题7分,共28分)
19.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.
20.如图,在△ABC中,AC=BC.
(1)尺规作图:在AC上找一点M,使得∠MBC=∠C;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若满足BM=AB时,求∠C的度数.
21.课间,小明拿着老师的等腰直角三角尺玩,不小心掉到两堆砖块之间,如图所示.
(1)求证:△ADC≌△CEB;
(2)已知DE=35cm,请你帮小明求出砖块的厚度a的大小(每块砖的厚度相同).
22.如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).
(1)你知道它们的对应点的坐标有什么关系吗?
(2)如果△ABC内有一点P(x,y),那么在△A′BC内P的对应点P′的坐标是什么?
五、解答题(每小题8分,共16分)
23.(1)证明角平分线具有的性质:角平分线上的点到角的两边的距离相等.
为了更直观、清楚地表达题意,我们通常在证明之前画出图形,并用符号表示已知和求证.
如图1,已知:OC平分∠AOB,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
(2)如图2,在△OAB中,OP平分∠AOB,交AB于点P,PD⊥OA于点D,PE⊥OB于点E,OA=OB=6,若S△OAB=15,求PD的长.
24.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,
求:(1)此时轮船与小岛P的距离BP是多少海里.
(2)小岛点P方圆3海里内有暗礁,如果轮船继续向东行驶,请问轮船有没有触礁的危险?说明理由.
六、解答题(每小题10分,共20分)
25.感知: 如图①,点E为等边三角形ABC中AC边上一点,连接BE,以BE为边在BE的左侧作等边三角形BDE,连接AD。
则∠DAE的度数为________;线段AC、AD、AE之间的数量关系为____________________。
探究:如图②,将图①中的△BAC和△BDE改为等腰直角三角形,其中∠ABC=∠DBE=90°,点E在AC边上,连接AD,请判断∠DAE的度数及线段AC、AD、AE之间的数量关系,并说明理由。
拓展:在②的条件下,若点E在线段CA的延长线或反向延长线上时,请直接写出AC、AD、AE之间的数量关系。
图① 图②
26.如图,△ABC是等边三角形,BC=12cm,动点M在AC上,由C向A运动,速度为2cm/s,同时点N以相同的速度在射线AB上从点B向AB的延长线方向运动,过点M作ME⊥BC,连接MN,设运动的时间为x秒。
(1)AM= ;CE= ;BE= 。(用含x的式子表示);
(2)当∠BND=30°时,求CM的长;
(3)在运动过程中,线段DE的长是否发生变化?如果不变,求出线段DE的长;如果发生变化,请说明理由。
参考答案与评分标准
一.选择题(每小题2分, 共12分)
1.B 2.B 3.D 4.A 5.B 6.C
二.填空题(每小题3分, 共24分)
7.105° 8. 6或8 9.﹣10 10.20 11.2 12.30° 13.70 14. 16
三、解答题(每小题5分,共20分)
15. 解:设这个多边形的边数是n,
依题意得(n﹣2)×180°=3×360°﹣180°, (3分)
n﹣2=6﹣1,
n=7.
∴这个多边形的边数是7. (5分)
16.解:(1)如图所示,△A1B1C1即为所求,点A关于x轴对称的点坐标为 (﹣1,﹣3);点B关于y轴对称的点坐标为:(﹣2,0),
故答案为:(﹣1,﹣3),(﹣2,0); (2分)
(4分)
(2)△ABC的面积是:4×5﹣12×2×4﹣12×3×3﹣12×1×5=9,
故答案为:9. (5分)
17. 证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∠CAD=∠BAD, (2分)
∴∠ADC=90°∴∠CAD+∠C=90°
∵BE⊥AC,∴∠BEC=90°
∴∠CBE+∠C=90°, (4分)
∴∠CBE=∠BAD. (5分)
18.解:∵AD∥BC,∴∠ADB=∠DBC,
又∵AB=AD,∴∠ADB=∠ABD,
∴∠DBC=∠ABD=30°, (2分)
∵DC⊥BC于点C,∴∠C=90°,
∵在Rt△BDC中,∠DBC=30°,BD=2, (4分)
∴CD=12BD,∴CD=1. (5分)
四、解答题(每小题7分,共28分)
19.(1)解:∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠C=70°
∵AB的垂直平分线MN交AC于点D,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=30° (4分)
(2)解:∵AE=6,
∴AC=AB=2AE=12,
∵△CBD的周长为20,
∴BC=20﹣(CD+BD)=20﹣(CD+AD)=20﹣12=8,
∴BC=8. (7分)
20.解:(1)如图所示:
作BC的垂直平分线交AC于点M,点M即为所求.
(3分)
(2)∵∠MBC=∠C,
∴BM=MC,设∠C=∠MBC=α,
∴∠BMA=2α,
又BM=AB,
则∠A=∠BMA=2α,
又AC=BC,
∴∠A=∠ABC=2α,
∴2α+2α+α=180°,解得:α=36°.∴∠C=36°. (7分)
21.(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,∠ADC=∠CEB∠DAC=∠BCEAC=BC,
∴△ADC≌△CEB(AAS); (4分)
(2)解:由题意得:
∵一块墙砖的厚度为a,∴AD=4a,BE=3a,
由(1)得:△ADC≌△CEB,
∴DC=BE=3a,AD=CE=4a,
∴DC+CE=BE+AD=7a=35,∴a=5,
答:砌墙砖块的厚度a为5cm. (7分)
22.解:(1)∵A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2),
∴它们的对应点的横坐标相等,纵坐标的和为6; (4分)
(2)由(1)可知P′的坐标为(x,6﹣y). (7分)
五、解答题(每小题8分,共16分)
23. (1)证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
∵OC平分∠AOB,
∴∠DOP=∠EOP,
在△PDO和△PEO中,∠PDO=∠PEO∠DOP=∠EOPOP=OP ,
∴△PDO≌△PEO(AAS),
∴PD=PE; (4分)
(2)解:∵OP平分∠AOB,PD⊥OB,PE⊥OA,
∴PD=PE,
∵OA=OB=6,
∴S△AOP=S△BOP,
∵S△OAB=15,
∴S△AOP=S△BOP=12×15=152,
∴12OA•PD=152,
∴6PD=15,
∴PD=52. (8分)
24.解:(1)过P作PD⊥AB于点D,
∵∠PBD=90°﹣60°=30°
且∠PBD=∠PAB+∠APB,∠PAB=90﹣75=15°
∴∠PAB=∠APB,
∴BP=AB=7(海里). (3分)
(2)作PD⊥AB于D,
∵A处测得小岛P在北偏东75°方向,
∴∠PAB=15°,
∵在B处测得小岛P在北偏东60°方向,
∴∠APB=15°,
∴AB=PB=7海里,
∵∠PBD=30°,
∴PD=12PB=3.5>3,
∴该船继续向东航行,没有触礁的危险. (8分)
六、解答题(每小题10分,共20分)
25.解:感知:120°,AC=AD+AE; (4分)
探究:∵∠ABC=∠DBE=90°,
∴∠ABD+∠ABE=∠ABE+∠CBE,
∴∠ABD=∠CBE,
∵△BAC和△BDE为等腰直角三角形,
∴AB=CB,DB=EB,∠BAC=∠C=45°,
∴△ABD≌△CBE, (6分)
∴∠BAD=∠C=45°,AD=CE,
∵∠DAE=∠BAD+∠BAC
∴∠DAE=45°+45°=90°
∵AC=AE+EC
∴AC=AE+AD (8分)
拓展:如图,E在CA的延长线上时,AD=AC+AE;
E在CA的反向延长线上时,AE=AC+AD。 (10分)
26. 解:(1)12-2x;x;12-x; (3分)
(2)∵△ABC为等边三角形,∴∠ABC=∠C=60°,
∵∠BND=30°,∴∠BDN=60°-30°=30°,
∴∠BND=∠BDN,∴BN=BD=2x,
∵∠C=60°,∠MDC=30°,
∴∠DMC=180°―60°―30°=90°
∴DC=2MC=4x,
∵BD+CD=BC=12,∴2x+4x=12,解得x=2,
∴CM=2x=4 (6分)
(3)线段DE的长度不发生变化;
在线段DE上截取PE=CE,连接PM,
∵ME⊥BC,PE=CE,
∴ME是PC的垂直平分线,
∴PM=CM,∴∠MPC=∠C=60°,
∴∠DBN=180°-60°=120°, ∠DPM=180°-60°=120°
∴∠DBN=∠DPM
∵BN=MC,∴PM=BN
又∵∠BDN=∠PDM,∴△BDN≌△PDM,∴PD=BD,
∵BC=BD+PD+PE+CE,∴BC=2DE,
∴DE=12÷2=6cm (10分)
相关试卷
这是一份2023-2024学年苏科版数学八年级上册期中测试卷,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年人教版数学八年级上册期末素质能力评价测试卷,共19页。试卷主要包含了恒成立,则下列关系式正确的是等内容,欢迎下载使用。
这是一份2023-2024学年人教版八年级上册 数学 期中培优训练,共5页。试卷主要包含了单选题,填空题,作图题,解答题等内容,欢迎下载使用。









