人教七上数学第三章一元一次方程章末复习导学案

章末复习

一、复习导入

1.导入课题：

同学们，学完本章内容后，你对本章的知识结构和知识要点以及知识运用等方面掌握得怎么样？还有哪些疑点？下面大家一起来走进本章的小结复习课堂，进行查漏补缺，完善本章的知识体系.

2.三维目标：

（1）知识与技能

①能够熟练地解一元一次方程；能够准确找出实际问题中的等量关系，建立方程模型；能够在解决实际问题的过程中，判断一个方程的解的合理性.

②能够体会方程是刻画现实世界的有效的数学模型，并在发现问题和解决问题的过程中寻求一种探究建立模型的方法.

（2）过程与方法

能够从日常生活中发现和提出与方程相关的问题，并尝试从不同的角度寻求解决问题的方法.

（3）情感态度

敢于面对解方程和建立方程模型过程中的各种困难，并有独立克服困难和运用知识解决问题的成功体验，对学习一元一次方程充满信心.

3.学习重、难点：

重点：一元一次方程的解法.

难点：一元一次方程的应用.

二、分层复习

1.复习指导：

（1）复习内容：教材第110页到第111页的内容.

（2）复习时间：5～8分钟.

（3）复习方法：阅读课本内容，通过回顾本章的知识展开过程，熟悉本章的知识点及运用.

（4）复习参考提纲：

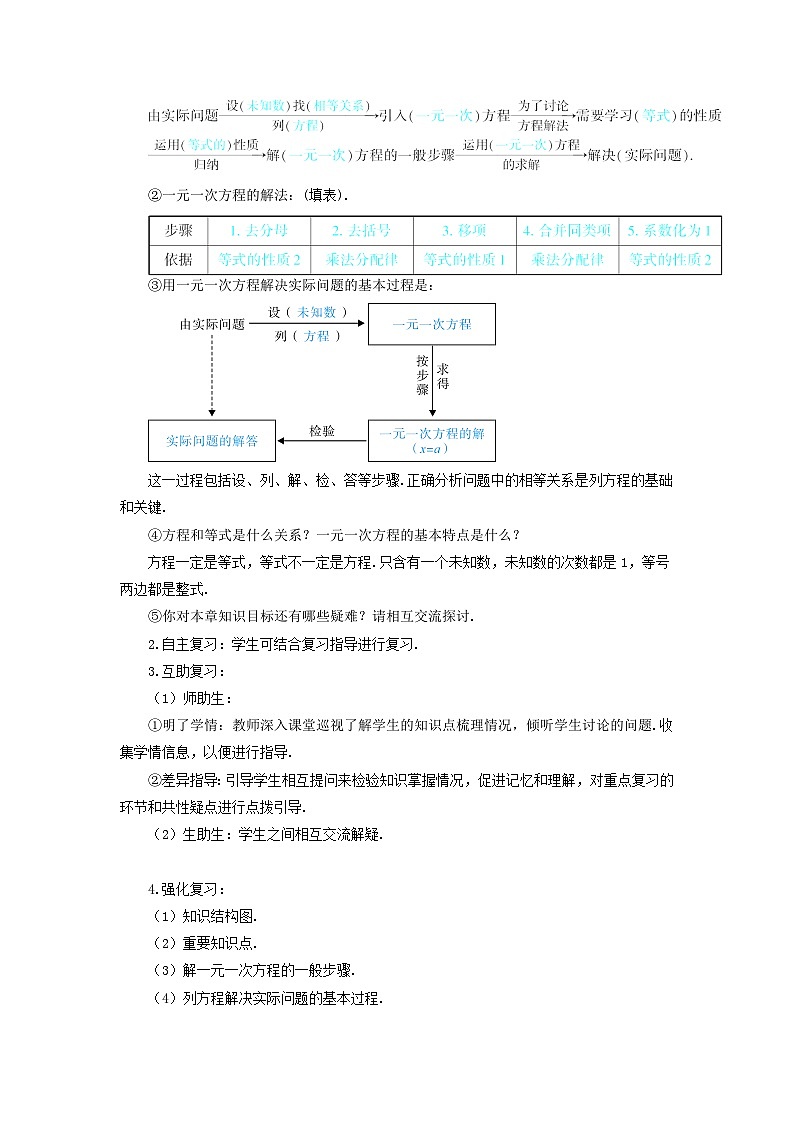
①回顾本章知识展开顺序，完成下列填空：

②一元一次方程的解法：(填表).

③用一元一次方程解决实际问题的基本过程是：

这一过程包括设、列、解、检、答等步骤.正确分析问题中的相等关系是列方程的基础和关键.

④方程和等式是什么关系？一元一次方程的基本特点是什么？

方程一定是等式，等式不一定是方程.只含有一个未知数，未知数的次数都是1，等号两边都是整式.

⑤你对本章知识目标还有哪些疑难？请相互交流探讨.

2.自主复习：学生可结合复习指导进行复习.

3.互助复习：

（1）师助生：

①明了学情：教师深入课堂巡视了解学生的知识点梳理情况，倾听学生讨论的问题.收集学情信息，以便进行指导.

②差异指导：引导学生相互提问来检验知识掌握情况，促进记忆和理解，对重点复习的环节和共性疑点进行点拨引导.

（2）生助生：学生之间相互交流解疑.

4.强化复习：

（1）知识结构图.

（2）重要知识点.

（3）解一元一次方程的一般步骤.

（4）列方程解决实际问题的基本过程.

1.复习指导:

（1）复习内容：典例分析.

（2）复习时间：8分钟.

（3）复习方法：按例题的分析引导，积极思考，然后尝试求解.

（4）复习参考提纲：

例1：已知x=－1是方程ax3＋bx－3=2的解，则当x=1时，求代数式ax3＋bx－3的值.

分析：根据方程解的意义，将x=－1代入方程中，然后比较所求的代数式可求值.

解：将x=-1代入方程a(-1)3+b(-1)-3=2,即a+b=-5.

当x=1时，原式=a·12+b·1-3=a+b-3=-8.

例2：在“五一”期间，小明、小亮等同学随家长一同到某公园游玩，下面是购买门票时，小明与他爸爸的对话(如图)试根据图中信息，解答下列问题：

①小明他们一共去了几个成人，几个学生？

8个成人，4个学生.

②请你帮助小明算一算，用哪种方式购票更省钱？说明理由.

分析：a.设成人的人数为x，则学生人数为12-x，根据总共的票价可列出方程：35x+17.5（12-x）=350.

b.算一算团体票的最少费用，再比较它与350的大小.

解：购买团体票，共需要花费的费用：35×16×0.6=336（元）＜350元.

答：买团体票便宜.

2.自主复习：同学们在自学指导下进行学习，力求独立求解，若有困难，可请教他人或相互协作完成.

3.互助复习：

（1）师助生：

①明了学情：教师深入课堂了解学生的学习进度，遇到的困难和出现的问题.

②差异指导：根据学情进行相应指导.

（2）生助生：小组内相互交流、研讨，互帮互学.

4.强化复习：

（1）各小组展示学习成果，得出例题的规范解答.

（2）练习：

三、评价

1.学生的自我评价：谈谈自己在本章复习小结学习中的态度、方法和成效.

2.教师对学生的评价：

（1）表现性评价：教师从总体和个体两个方面对学生在学习中的态度、学法和成效等进行总结.

（2）纸笔评价：课堂评价检测.

3.教师的自我评价（教学反思）：

本课时的复习目的是使学生进一步系统掌握方程知识，学会用一元一次方程解决实际问题的基本技能和基本方法，进一步提高综合应用数学知识、灵活地分析和解决问题的能力.要抓住应用问题的基本类型和一般等量关系，利用知识间的联系加强理解，便于实际应用，提高计算能力.

一、基础巩固

1.（10分）已知4x2n－5+5=0 是关于x 的一元一次方程，则n ＝3.

2.（10分）当x＝时，代数式x－1 和的值互为相反数.

3.（10分）某商品的进价是1000元，售价为1500元，由于销售情况不好，商场决定降价出售，但又要保证利润不低于15%，那么商场最多降350元出售此商品.

4.（10分）对方程[－(2x－3)]= 变形，第一步较好的方法是（A）

A.去分母    B.去括号    C.移项    D.合并同类项

5.（10分）为鼓励居民节约用水，对自来水用户按分段计费方式收取水费：若每月用水不超过7立方米，则按每立方米1元收费，若每月用水超过7立方米，则超过部分按每立方米2元收费.如果某用户今年5月缴纳17元水费，那么这户居民今年5月份的用水量为12立方米.

二、综合应用

7.（20分）小刚和小强从A、B两地同时出发，小刚骑自行车，小强步行，沿同一条路线相向匀速而行，出发后2 h两人相遇，相遇时小刚比小强多行进24 km，相遇后0.5 h小刚到达B地，两人的行进速度分别是多少？相遇后经过多少时间小强到达A地？

解：设相遇时小强行进的路程为x km，小刚行进的路程为（x+24） km，小强行进的速度为 km/h，小刚行进的速度为km/h.

三、拓展延伸

8.（10分）甲、乙两家超市以相同的价格出售同样的商品，为了吸引顾客，各自推出了不同优惠方案：在甲超市累计购买商品超过300元后，超过部分按原价8折优惠；在乙超市累计购买商品超过200元后，超出部分按原价8.5折优惠，若顾客累计购买商品x(x≥300) 元.

（1）用含x 的式子分别表示顾客在甲、乙两家超市的费用.

（2）当x为多少时，两家超市费用一样多.

（3）当x＝500时，选择哪家超市优惠？说明理由.

（4）当x＝1000时，选择哪家超市优惠？说明理由.

解：（1）甲家：300+0.8×（x-300）=0.8x+60乙家：200+0.85（x-200）=0.85x+30

（2）0.8x+60=0.85x+30解得：x=600.

(3)选择乙家比较优惠

甲：300+0.8×（500-300）=460（元）;

乙：200+0.85×（500-200）=455（元）

∴选乙家.

（4）选择甲家比较优惠.

甲：300+0.8×（1000-300）=860（元）;

乙：200+0.85×（1000-200）=880（元）

∴选甲家.