人教版11.2.1 三角形的内角教学课件ppt

这是一份人教版11.2.1 三角形的内角教学课件ppt，共16页。PPT课件主要包含了“8”字模型，∠C∠D90°，∠A∠C，AC∥CD，∠B∠D，直角形，三角形内角和180°，直角三角形等内容，欢迎下载使用。

11.2.1 直角三角形的内角(第2课时)
能运用直角三角形的性质与判定.体会整体思想、方程思想和模型思想.
观察我们常用的一副三角板,思考下列问题：
(1) 两锐角的度数之和为多少度?(2) 任意的直角三角形的两锐角的度数之和为多少度?说说理由.(3) 你从中还得出什么结论？
如图, 在直角三角形ABC 中，∠C = 90°， 由三 角形内角和定理，得∠A+ ∠ B+ ∠C = 180°,∠A+ ∠ B= 180°-∠C ,∠A+ ∠ B= 180°-90° ,∴ ∠ A + ∠ B = 90°
直角三角形的两个锐角互余．
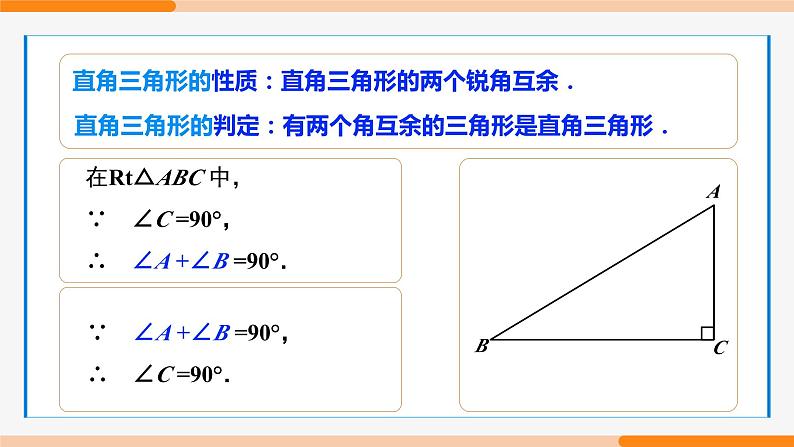
直角三角形的性质：直角三角形的两个锐角互余．　　
在Rt△ABC 中，∵　∠C =90°，∴　∠A +∠B =90°．　
你还得出什么结论？说说你的理由.
直角三角形的判定：有两个角互余的三角形是直角三角形．　　
∵　∠A +∠B =90°，∴　∠C =90°．　
2．具备下列条件的△ABC中，不是直角三角形的是(　　)A．∠A＋∠B＝∠CB．∠A＝ ∠B＝ ∠CC．∠A∶∠B∶∠C＝1∶2∶3D．∠A＝2∠B＝3∠C
1. 如图所示，△ABC为直角三角形，∠ACB=90°， CD⊥AB，与∠1互余的角有（　　）A．∠B B．∠A C．∠BCD和∠A D．∠BCD
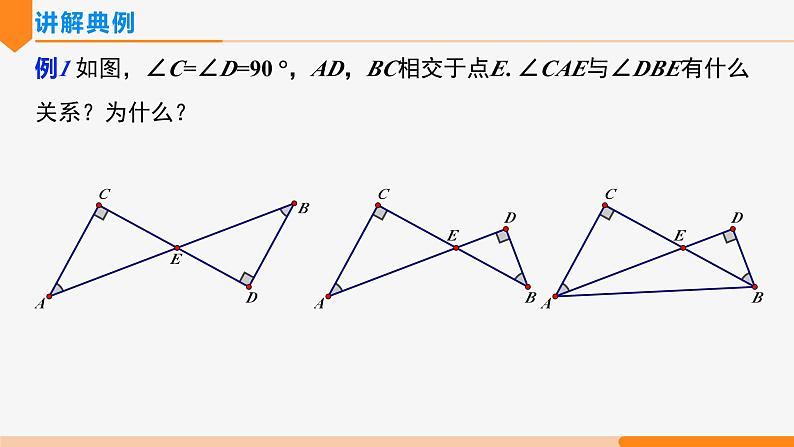
例1 如图，∠C=∠D=90 °，AD，BC相交于点E. ∠CAE与∠DBE有什么关系？为什么？
∠A+∠B=∠C+∠D
例2 如图，∠C=90 °, ∠1= ∠2，△ADE是直角三角形吗？为什么？
解：在Rt△ABC中，
∴∠2+ ∠A=90 ° ∵ ∠1= ∠2, ∴∠1 + ∠A=90 °.即 △ADE是直角三角形.
变式 如图，∠C=90 °, ∠1= ∠2，△CDE是直角三角形吗？为什么？
直 角 形
直角三角形的两个锐角互余
有两个角互余的三角形是直角三角形
1．如图，AD是Rt△ABC的斜边BC上的高，则图中与∠B互余的角有(　 )A．1个 B．2个 C．3个 D．4个
3．下列△ABC中，不是直角三角形的是(　　)A．∠A＝90° B．∠A∶∠B∶∠C＝3∶4∶5C．∠C＝∠A＋∠B D．∠A＋∠C＝90°
2.在△ABC中，若∠A=43°，∠B=47°，则这个三角形是________.
4．如图，BD平分∠ABC，∠ADB＝60°，∠BDC＝80°，∠C＝70°.试判断△ABD的形状．
解：在△DBC中，∠DBC＝180°－∠BDC－∠C ＝180°－80°－70°＝30°.∵ BD平分∠ABC，∴∠ABD＝∠DBC＝30°. 在△ABD中， ∵∠ADB＋∠ABD＝60°＋30°＝90°，∴△ABD是直角三角形．