初中数学人教版八年级上册12.2 三角形全等的判定教学课件ppt

这是一份初中数学人教版八年级上册12.2 三角形全等的判定教学课件ppt，共17页。PPT课件主要包含了动手操作，归纳知识，三角形全等判定，归纳方法，角相等，条件1，条件2，条件3，全等三形角，边相等等内容，欢迎下载使用。

12.2 三角形全等的判定(第2课时)
判定两三角形全等的基本事实：边角边全等三角形判定“边角边”的简单应用了解“SSA”不能作为两个三角形全等的条件．
1. 边边边判定定理的内容是什么？怎样书写？
2. 怎样得到 边边边判定定理？
复习边边边判定，回答下列问题
三边对应相等的两个三角形全等(简写为“边边边”或“SSS”)
在△ABC和△ DEF中，
∴ △ABC ≌△ DEF（SSS）.
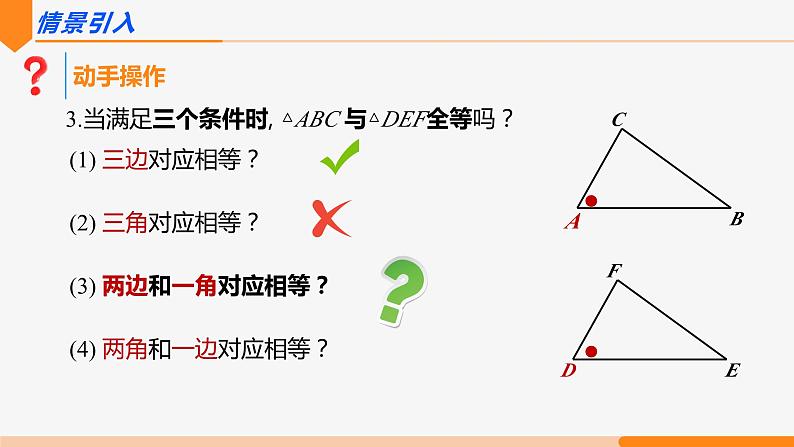
3.当满足三个条件时, △ABC 与△DEF全等吗？
(1) 三边对应相等？
(3) 两边和一角对应相等？
(2) 三角对应相等？
(4) 两角和一边对应相等？
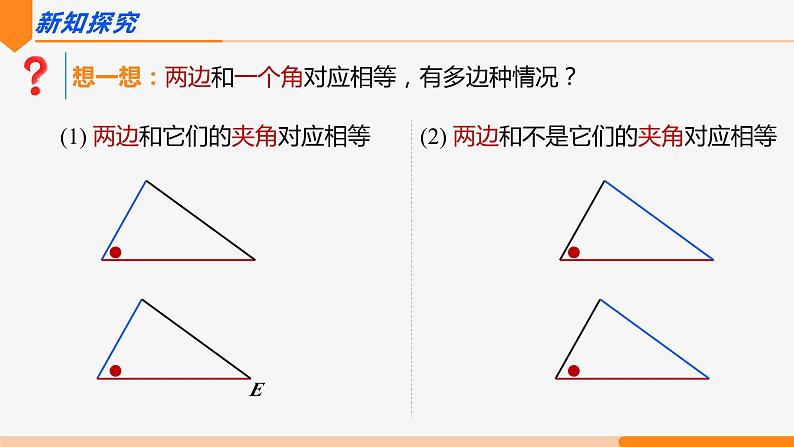
想一想：两边和一个角对应相等，有多边种情况？
(1) 两边和它们的夹角对应相等
(2) 两边和不是它们的夹角对应相等
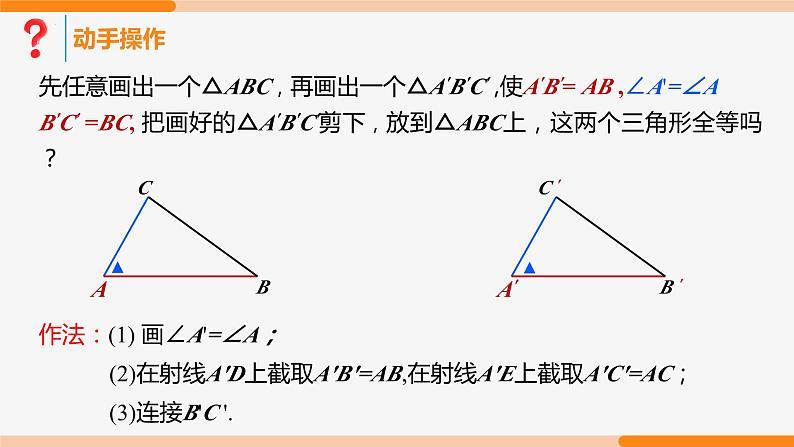
先任意画出一个△ABC，再画出一个△A′B′C′ ,使A′B′= AB ,∠A'=∠AB′C′ =BC, 把画好的△A′B′C′剪下，放到△ABC上，这两个三角形全等吗？
作法：(1) 画∠A'=∠A；(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC；(3)连接B'C '.
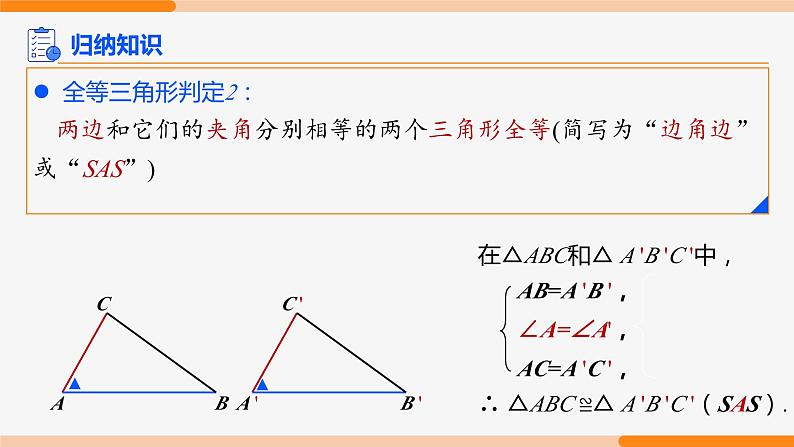
全等三角形判定2：两边和它们的夹角分别相等的两个三角形全等(简写为“边角边”或“SAS”)
在△ABC和△ A 'B 'C '中，
∴ △ABC ≌△ A 'B 'C '（SAS）.
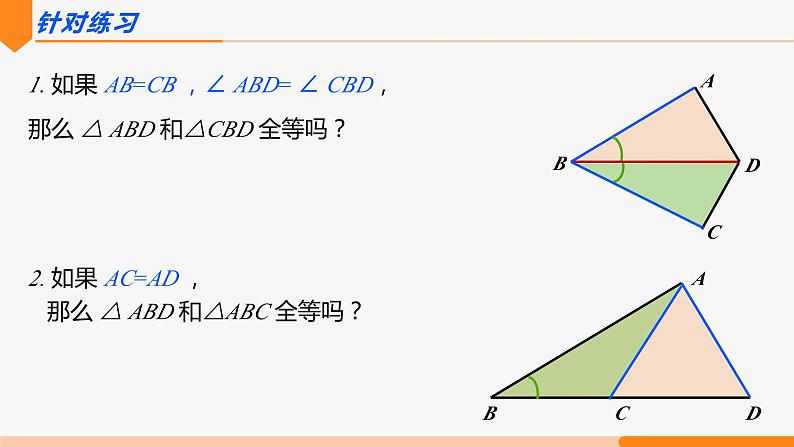
1. 如果 AB=CB ，∠ ABD= ∠ CBD，那么 △ ABD 和△CBD 全等吗？
2. 如果 AC=AD ，那么 △ ABD 和△ABC 全等吗？
有两边和其中一边的对角分别相等的两个三角形不一定全等.
若 AC=AD ，则 △ ABD 和△ABC 不一定全等
例1：如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连接AC并延长到点D，使CD＝CA，连接BC并延长到点E，使CE＝CB．连接DE，那么量出DE的长就是A、B的距离，为什么?
解：在△ABC 和△DEC 中，
∴ △ABC ≌△DEC（SAS），∴ AB =DE （全等三角形的对应边相等）.
全 等 三 形 角
例2：已知:如图, AB=DB,CB=EB,∠1＝∠2，求证:∠A=∠D.
证明:∵ ∠1＝∠2(已知)， ∴∠1+∠DBC＝ ∠2+ ∠DBC(等式的性质)， 即∠ABC＝∠DBE. 在△ABC和△DBE中, AB＝DB， ∠ABC＝∠DBE(已证)， CB＝EB， ∴△ABC≌△DBE(SAS). ∴ ∠A=∠D(全等三角形的对应角相等).
有两边及夹角对应相等的两个三角形全等（简写成SAS)
1. 已知两边，必须找“夹角”2. 已知一角和这角的一夹边，必须找这角的另一夹边
如图，a，b，c 分别表示△ABC的三边长，则下面与△ABC一定全等的三角形是(　　)
2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( ) A.∠A＝∠D B.∠E＝∠C C.∠A=∠C D.∠ABD＝∠EBC  
3. 如图，AA′，BB′表示两根长度相同的木条，若O是 AA′，BB′的中点，经测量AB=9 cm，则容器的内 径A′B′为(　　) A．8 cm　　B．9 cm　　C．10 cm　　D．11 cm
4. 下列条件中，不能证明△ABC≌△DEF的是(　　)
A．AB＝DE，∠B＝∠E，BC＝EFB．AB＝DE，∠A＝∠D，AC＝DFC．BC＝EF，∠B＝∠E，AC＝DFD．BC＝EF，∠C＝∠F，AC＝DF
4.如图，点E、F在AC上，AD//BC，AD=CB，AE=CF. 求证：△AFD≌△CEB.
在△AFD和△CEB中，
∴△AFD≌△CEB（SAS）.
∴ AE+EF=CF+EF，