人教版八年级上册13.3.2 等边三角形教学ppt课件

这是一份人教版八年级上册13.3.2 等边三角形教学ppt课件，共18页。PPT课件主要包含了等腰三角形的判定，复习旧知，等腰三角形，两腰相等，三线合一，等边对等角，证边相等，证角相等，对称轴，两边相等等内容，欢迎下载使用。
探索等边三角形的性质和判定．能运用等边三角形的性质和判定进行计算和证明．
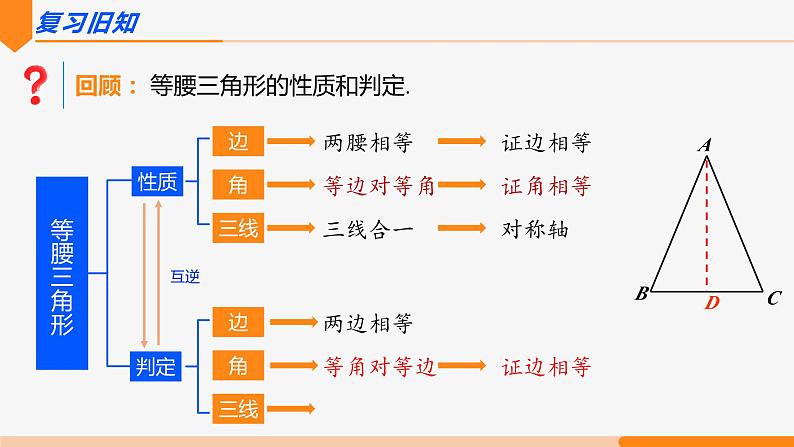
回顾： 等腰三角形的性质和判定.
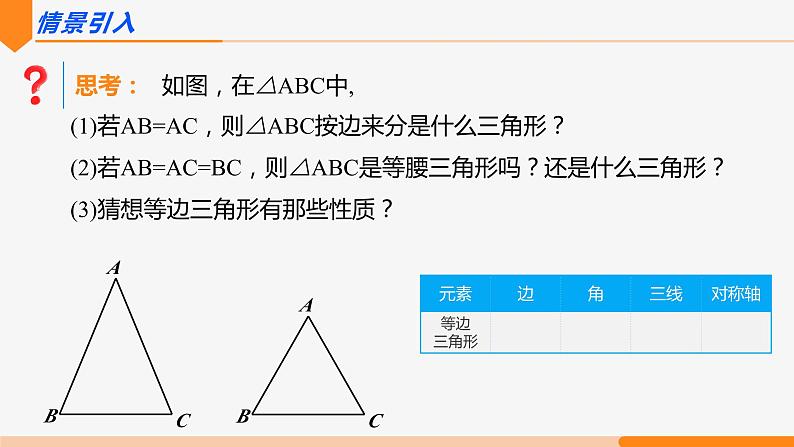
思考： 如图，在△ABC中,
(1)若AB=AC，则△ABC按边来分是什么三角形？(2)若AB=AC=BC，则△ABC是等腰三角形吗？还是什么三角形？(3)猜想等边三角形有那些性质？
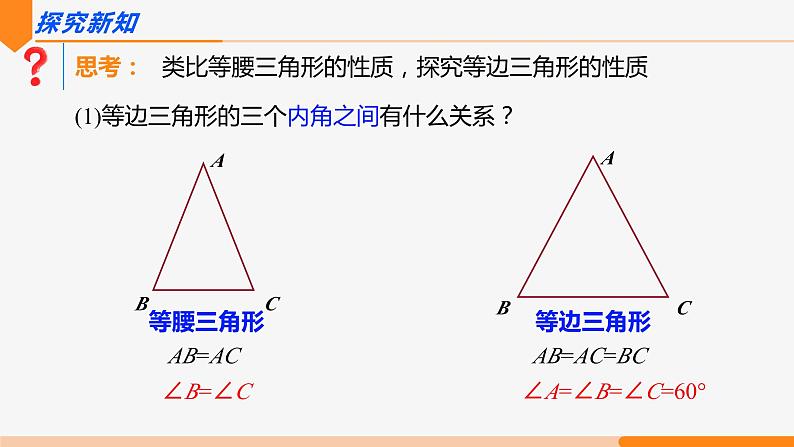
∠A=∠B=∠C=60°
思考： 类比等腰三角形的性质，探究等边三角形的性质
(1)等边三角形的三个内角之间有什么关系？
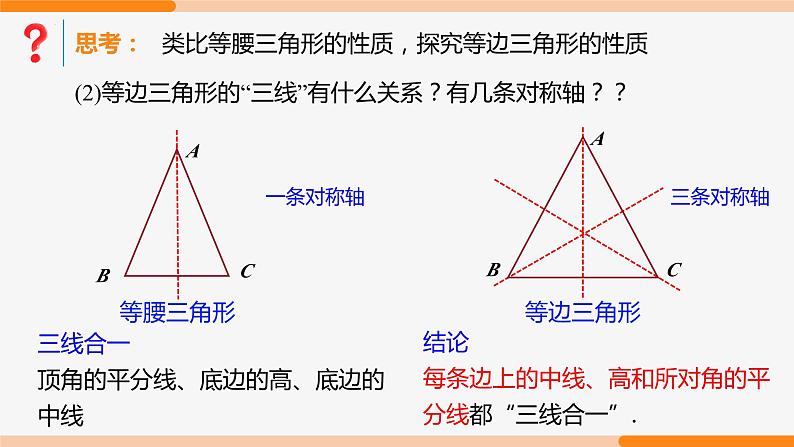
(2)等边三角形的“三线”有什么关系？有几条对称轴？？
结论每条边上的中线、高和所对角的平分线都“三线合一”.
底边上的中线、高和顶角的平分线互相重合
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等，且都是60º
例1 如图，△ABC是等边三角形，D，E，F分别是三 边AB，AC，BC上的点，且DE⊥AC，EF⊥BC， DF⊥AB，计算△DEF 各个内角的度数．
解：∵ △ABC是等边三角形， ∴ ∠A＝∠B＝∠C＝60°. ∵ DE⊥AC，EF⊥BC，DF⊥AB， ∴ ∠AED＝∠EFC＝∠FDB＝90°， ∴ ∠ADE＝90°－∠A＝90°－60°＝30°， ∴ ∠EDF＝180°－30°－90°＝60°. 同理可得∠DEF＝∠EFD＝60°. 即△DEF各个内角的度数都是60°.
有一个角是60°的等腰三角形是等边三角形.
1.根据条件判断下列三角形是否为等边三角形.
例2 如图,在等边三角形ABC中，DE∥BC, 求证：△ADE是等边三角形.
∵ △ABC是等边三角形，
∴ ∠A= ∠B= ∠C.
∴ ∠ADE= ∠B, ∠AED= ∠C.
∴ ∠A= ∠ADE= ∠AED.
∴ △ADE是等边三角形.
变式1 如图,在等边三角形ABC中，补充一条件，使用△ADE是等边三角形，并证明你的结论。
解：当BD=CE时，△ADE是等边三角形，其理由如下：
∴ ∠A=60°，AB=AC.
∴ AB－BD= AC－CE，即AD= AE.
变式2 如图,在等边三角形ABC中，若点D、E 分别在边AB、AC 的延长线上DE∥BC, 则△ADE是等边三角形，结论还成立吗？
证明∵　△ABC 是等边三角形， ∴　∠A =∠ABC =∠ACB =60°． ∵　DE∥BC， ∴　∠ABC =∠ADE， ∠ACB =∠AED. ∴　∠A =∠ADE =∠AED. ∴　△ADE 是等边三角形.
1.如图，△ABC是等边三角形，点D在AC边上， ∠DBC＝35°，则∠ADB的度数为(　　) A．25° B．60° C．85° D．95°
2.如图，一个等边三角形纸片，剪去一个角后得到 一个四边形，则图中∠α＋∠β的度数是(　　)A．180° B．220° C．240° D．300°
3.如图,△ABC和△ADE都是等边三角形，已知△ABC的周长为18 cm，EC =2 cm，则△ADE的周长是 cm.
4.如图，在等边△ABC中，BD平分∠ABC，BD=BF，则∠CDF的度数是（　　）A．10° B．15° C．20° D．25°
5.如图，等边△ABC中，D、E、F分别是各边上的一点，且AD=BE=CF．求证：△DEF是等边三角形．
证明∵△ABC为等边三角形，且AD=BE=CF，∴AF=BD=CE，∠A=∠B=∠C=60°，∴△ADF≌△BED≌△CFE（SAS），∴DF=ED=FE，∴△DEF是等边三角形．