人教版13.4课题学习 最短路径问题教学ppt课件

这是一份人教版13.4课题学习 最短路径问题教学ppt课件，共20页。PPT课件主要包含了将军饮马，情景引入，问题将军饮马，复习旧知，新知探究，归纳知识，得交点，典例讲解，课堂小结，课堂练习等内容，欢迎下载使用。
能利用轴对称解决简单的最短路径问题.体会图形的变化在解决最值问题中的作用，感悟转化思想．
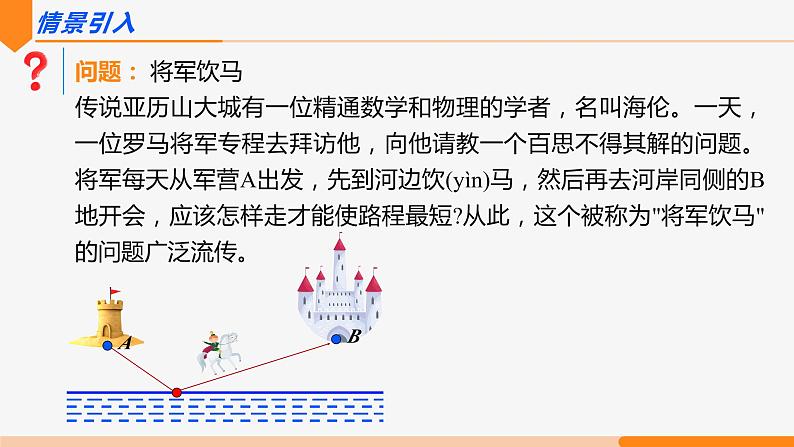
传说亚历山大城有一位精通数学和物理的学者，名叫海伦。一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题。将军每天从军营A出发，先到河边饮(yìn)马，然后再去河岸同侧的B地开会，应该怎样走才能使路程最短?从此，这个被称为"将军饮马"的问题广泛流传。
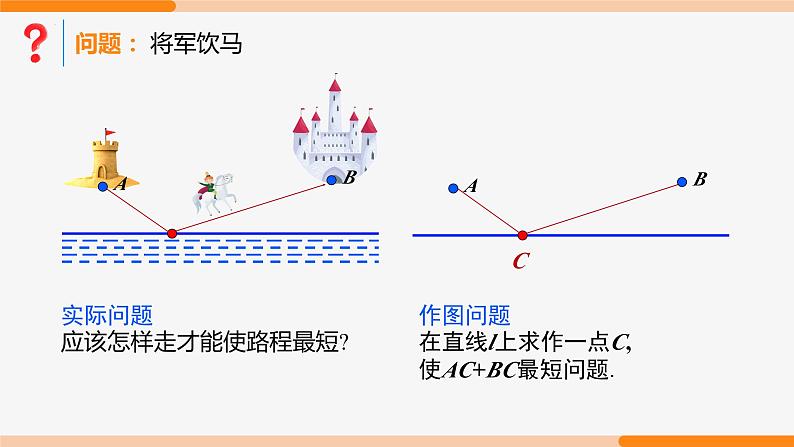
实际问题 应该怎样走才能使路程最短?
作图问题 在直线l上求作一点C,使AC+BC最短问题.
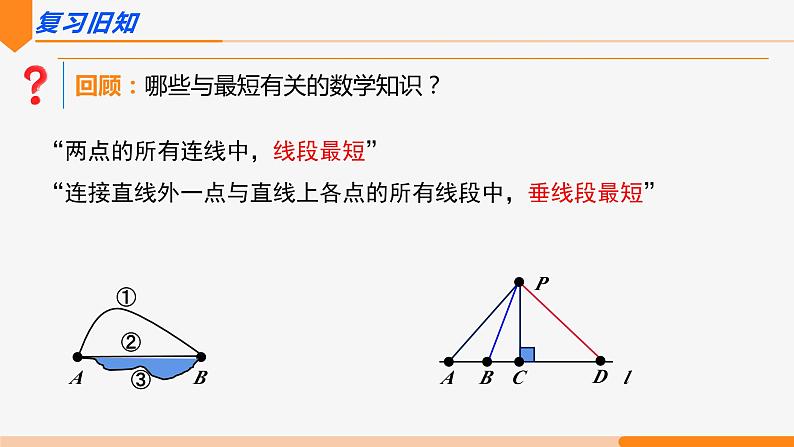
回顾：哪些与最短有关的数学知识？
“两点的所有连线中，线段最短”“连接直线外一点与直线上各点的所有线段中，垂线段最短”
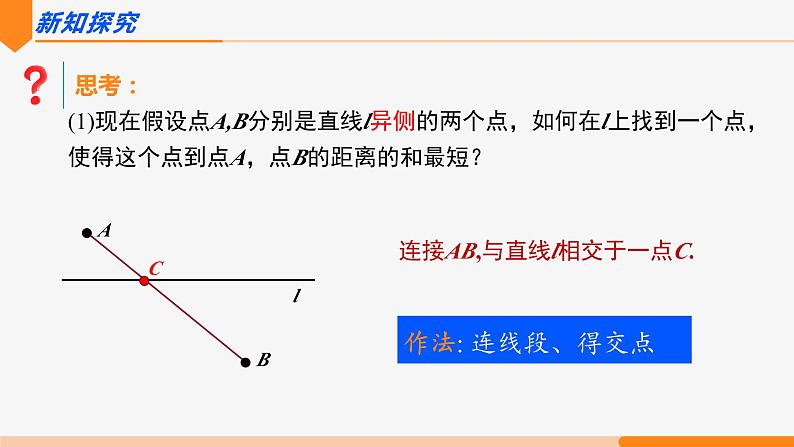
(1)现在假设点A,B分别是直线l异侧的两个点，如何在l上找到一个点，使得这个点到点A，点B的距离的和最短？
连接AB,与直线l相交于一点C.
作法: 连线段、得交点
(2)现在假设点A,B分别是直线l同侧的两个点，如何在l上找到一个点，使得这个点到点A，点B的距离的和最短？
作法：（1）作点B 关于直线l 的对称点B′；（2）连接AB′，与直线l 相交于点C． 则点C 即为所求．
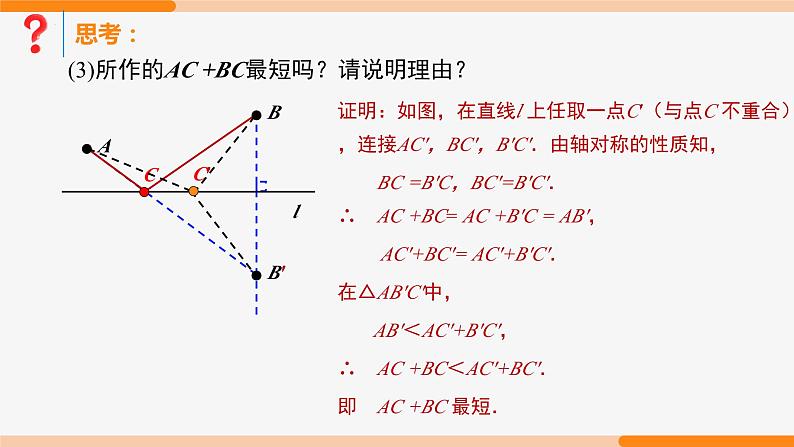
(3)所作的AC +BC最短吗？请说明理由？
证明：如图，在直线l 上任取一点C′（与点C 不重合），连接AC′，BC′，B′C′．由轴对称的性质知， BC =B′C，BC′=B′C′．∴　AC +BC= AC +B′C = AB′， AC′+BC′= AC′+B′C′．在△AB′C′中，AB′＜AC′+B′C′，∴　AC +BC＜AC′+BC′．即　AC +BC 最短．
作法: 作对称、连线段、得交点
两点之间线段最短(化折为直)
求作一点C,使AC+BC最短问题.
作对称、连线段、得交点
例1 如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，AD=5，点F是AD边上的动点，则BF+EF的最小值为（　　）A．7.5 B．5 C．4 D．不能确定
例2 （1）如图①，在AB直线一侧C、D两点，在AB上找一点P，使C、D、P三点组成的三角形的周长最短，找出此点，并说明理由；（2）如图②，在∠AOB内部有一点P，是否在OA、OB上分别存在点E、F，使得E、F、P三点组成的三角形的周长最短，找出E、F两点，并说明理由；（3）如图③，在∠AOB内部有两点M、N，是否在OA、OB上分别存在点E、F，使得E、F、M、N四点组成的四边形的周长最短，找出E、F两点，并说明理由．
此类求线段和的最小值问题，找准对称点是关键，而后将求线段长的和转化为求某一线段的长，而再根据已知条件求解.
1.如图，直线l是一条河，P、Q是两个村庄.欲在l上的某处修建一个水泵站，向P、Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需要管道最短的是（ ）
2．直线l外不重合的两点A，B，在直线l上求作一点C，使得AC＋BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是(　　)
A．转化思想B．三角形的两边之和大于第三边C．两点之间，线段最短D．三角形的一个外角大于与它不相邻的任意一个内角
3. 如图，在直角坐标系中，点A，B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A，B，C三点不在同一条直线上，当△ABC的周长最小时点C的坐标是（　　）A．（0，3） B．（0，2） C．（0，1） D．（0，0）
4．如图，在△ABC中，AB＝5，BC＝4，AC＝3.(1)用直尺和圆规作边AB的垂直平分线MN；(2)在直线MN上找一点D，使△ADC的周长最小，并求出△ADC的最小周长
解：(1)边AB的垂直平分线MN如图所示．
(2)如图，点D为MN与BC的交点．∵MN垂直平分AB，∴AD＝BD.∴△ADC的最小周长为AC＋BC＝3＋4＝7.