2023九年级数学上册第23章图形的相似相似三角形的判定课后练习二含解析新版华东师大版

这是一份2023九年级数学上册第23章图形的相似相似三角形的判定课后练习二含解析新版华东师大版，共5页。
相似三角形的判定 重难点易错点解析题一：题面：如图，平行四边形ABCD中，过点B的直线与对角线AC、边AD分别交于点E和F．过点E作EG∥BC，交AB于G，则图中相似三角形有（    ）．A．4对      B．5对      C．6对      D．7对 金题精讲题一：题面：如图，在△ABC中，AB=5，AC=4，点D在边AB上，∠ACD=∠B，则AD的长为        ． 题二：题面：在直角梯形ABCD中，AD∥BC，以AB为直径作圆O恰好与CD相切于E，连AC、BD相交于F，连EF．
（1）求证：AB2=4AD•BC；
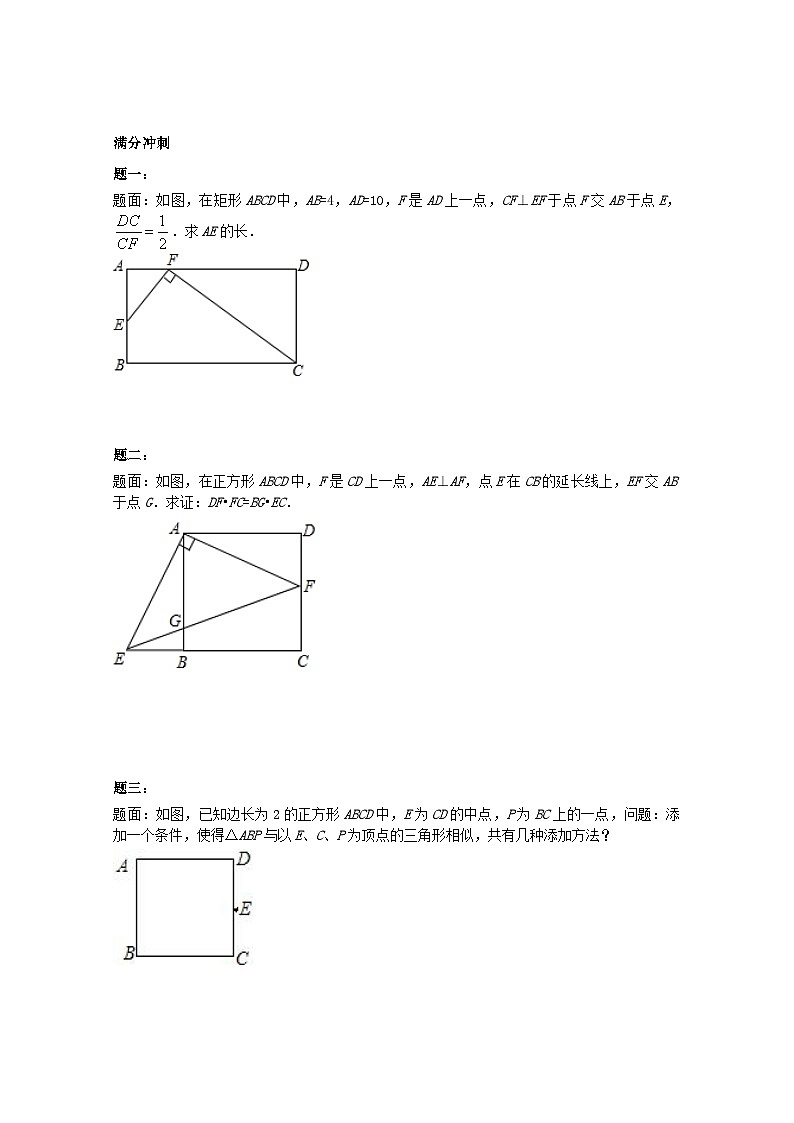
（2）求证：EF∥BC． 满分冲刺题一：题面：如图，在矩形ABCD中，AB=4，AD=10，F是AD上一点，CF⊥EF于点F交AB于点E， ．求AE的长．  题二：题面：如图，在正方形ABCD中，F是CD上一点，AE⊥AF，点E在CB的延长线上，EF交AB于点G．求证：DF•FC=BG•EC．   题三：题面：如图，已知边长为2的正方形ABCD中，E为CD的中点，P为BC上的一点，问题：添加一个条件，使得△ABP与以E、C、P为顶点的三角形相似，共有几种添加方法？  课后练习详解重难点易错点解析题一：答案：B．详解：根据平行四边形的性质，平行的性质和相似三角形的判定可得：△AGE∽△ABC，△BGE∽△BAF，△AEF∽△CEB，△ACB∽△CAD，△AGE∽△CDA，5对．故选B．金题精讲题一：答案：3.2．详解：∵∠ACD=∠B ，∠A=∠A，∴△ABC∽△ACD．∴．又∵AB=5，AC=4，∴，解得AD=3.2．题二：答案：AB2=4AD•BC；EF∥BC．详解：证明：（1）作DH⊥BC于H，如图，
∵梯形ABCD为直角梯形，且AD∥BC，
∴四边形ABHD为矩形，
∴DH=AB，AD=BH，
∴CH=CBAD，
∵以AB为直径作圆O恰好与CD相切于E，
∴DA、CB都是⊙O的切线，
∴DE=DA，CE=CB，∴DC=DA+CB，
在Rt△DHC中，DH2=DC2CH2，
∴AB2=(AD+BC)2(BCAD)2，
∴AB2=4AD•BC；
（2）∵AD∥BC，
∴△FDA∽△FBC，
∴，
而DE=AD，EC=BC，
∴，
∴EF∥BC． 满分冲刺题一：答案：．详解：∵四边形ABCD是矩形，
∴∠A=∠D=90°，DC=AB=4，
∵CF⊥EF，
∴∠EFC=90°．
∴∠AFE+∠DFC=90°，
∵∠AEF+∠AFE=90°，
∴∠AEF=∠DFC，
∴△AEF∽△DFC．
∴，
∵，DC=4，
∴∠DFC=30°，∴，
∴，
∴．题二：答案：DF•FC=BG•EC．详解：∵∠EAB+∠BAF=90°，∠DAF+∠BAF=90°，
∴∠BAE=∠DAF，
∴tan∠BAE=tan∠DAF，
∵AB=AD，
∴DF=BE，
又∵AB∥CD，
∴，
∴BE•FC=BG•EC，
∴DF•FC=BG•EC．题三：答案：只有一种方法在BC上的一点使得BP=．详解：如图
设BP=x，若△ABP∽△ECP，
得，即，解得x=．
若△PBA∽△ECP，得，即，
化简得x22x+2=0，此方程无解，故不存在
综上，只有一种方法在BC上的一点使得BP=．
（或延长AB至M，使BM=BA，连接EM，交BC与点P，则P就是符合条件的点）