湘教版九年级上册4.3 解直角三角形习题课件ppt

这是一份湘教版九年级上册4.3 解直角三角形习题课件ppt，共18页。PPT课件主要包含了∴BCCD－BD，∴∠ACB≈53°等内容，欢迎下载使用。
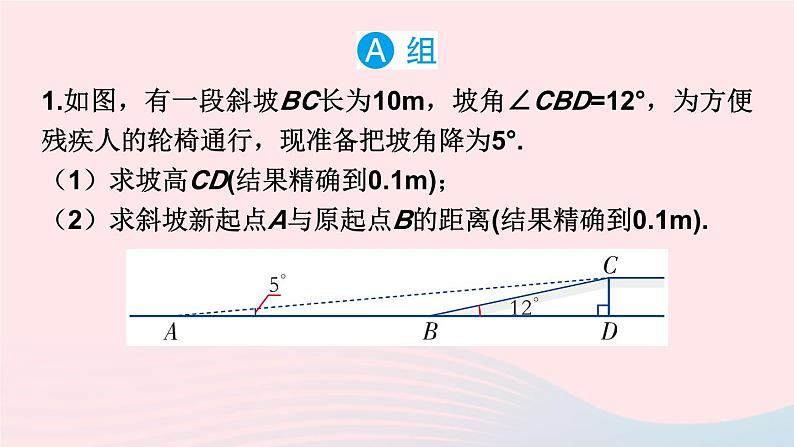
1.如图，有一段斜坡BC长为10m，坡角∠CBD=12°，为方便残疾人的轮椅通行，现准备把坡角降为5°.（1）求坡高CD(结果精确到0.1m)；（2）求斜坡新起点A与原起点B的距离(结果精确到0.1m).
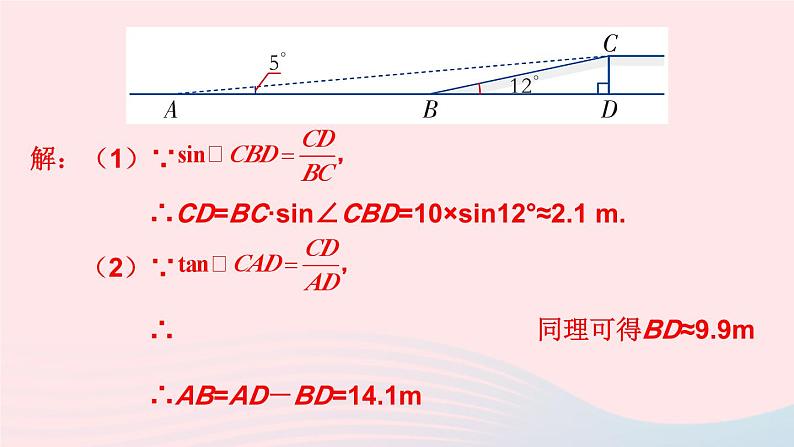
∴CD=BC·sin∠CBD=10×sin12°≈2.1 m.
同理可得BD≈9.9m
∴AB=AD－BD=14.1m
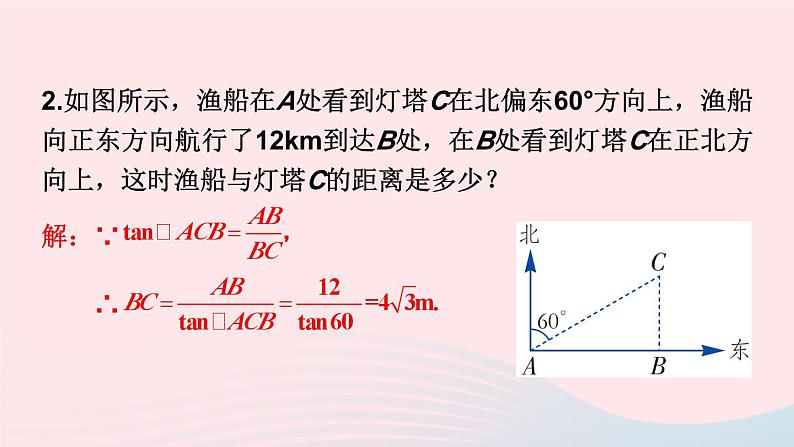
2.如图所示，渔船在A处看到灯塔C在北偏东60°方向上，渔船向正东方向航行了12km到达B处，在B处看到灯塔C在正北方向上，这时渔船与灯塔C的距离是多少？
3.图（1）是一间安装有壁挂式空调的卧室的一部分，图（2）是该空调挂机的侧面示意图. 已知空调挂机底部BC垂直于墙面CD，且当导风板所在直线AE与竖直线AB的夹角α为40°时，空调风刚好吹到床的外边沿E处.若AB=0.02m，BC=0.2m，床铺长DE=2.3m，求空调挂机底部位置距离床的高度CD（结果精确到0.1m）.
解：设射线AB交DE于点F，由题意得，DF=0.2m，CD=BF，
∵EF=DE－DF=2.3－0.2=2.1(m)，
∴BF≈2.5(m)，
∴CD=BF≈2.5(m)，
∴空调挂机底部位置距离床的高度CD约为2.5m.
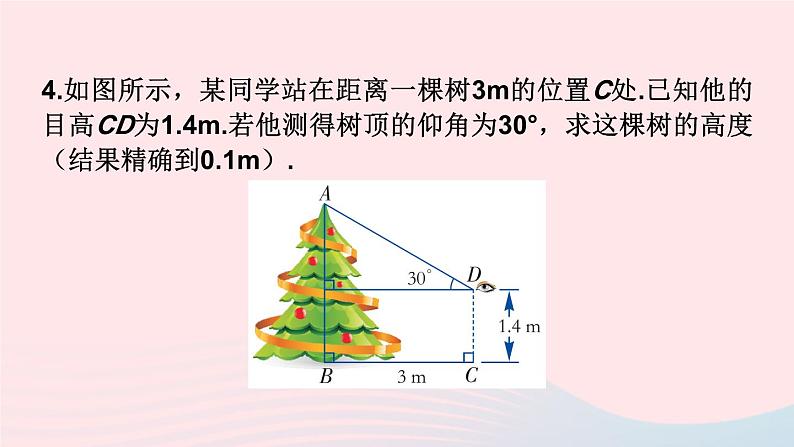
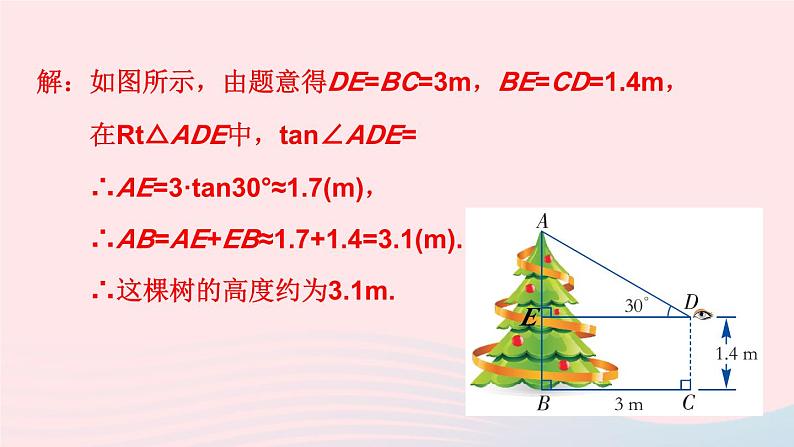
4.如图所示，某同学站在距离一棵树3m的位置C处.已知他的目高CD为1.4m.若他测得树顶的仰角为30°，求这棵树的高度（结果精确到0.1m）.
解：如图所示，由题意得DE=BC=3m，BE=CD=1.4m，
∴AE=3·tan30°≈1.7(m)，
∴AB=AE+EB≈1.7+1.4=3.1(m).
∴这棵树的高度约为3.1m.
5.如图，塔AD的高度为30m，塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB，∠EAC分别为60°和 30°.求BD，BC的长(结果精确到0.01 m).
解：由题意得∠BAD=90°－60°=30°， ∠CAD=90°－30°=60°，
6.如图（a），A，B和C是三个小岛．一艘船由A处出发向正东方向航行4km到达B处，然后向正北方向航行3km到达C处.（1）求由A测得C的方位角的大小（结果精确到1°）.
∴由A测得C的方位角的大小约为53°.
（2）如图（b），直升机由C飞往A，其飞行高度一直保持在海平面以上的h km.当直升机飞到P处时，由Р测得C和A的俯角分别是48°和65°.已知A，C，P和海平面上一点M都在同一个平面上，且M位于P的正下方，求h（结果精确到0.1km）.
解：由题意得，∠PAM=65°，∠PCM=48°，
在Rt△ABC中，∵AB=4 km，BC=3 km，
∵AC=AM+CM，即5=0.5h+0.9h，
∴h≈3.6(km).
7.如图，MN表示水平地面，由地面上A处测得山上B处的仰角是25°，由山顶C处测得B处的俯角是40°.若AB∶BC=2∶3，求由A处测得C处的仰角（结果精确到0.1°）.
解：如图，过点B作BD⊥MN于点D，并反向延长BD交CE于点E，则BE⊥CE，过点C作CF⊥MN于点F，则CF=DE，CE=FD，
∵AB∶BC=2∶3，
∴设AB=2k，则BC=3k，
∴AD=2k·cs25°≈1.8k，
∴BD=2k·sin25°≈0.8k，
∴CE=3k·cs40°≈2.3k，
∴DF=CE≈2.3k，
∴BE=3k·sin40°≈1.9k，