海南省东方市2023届九年级上学期期末检测数学试卷(含解析)

2022-2023学年海南省东方市九年级第一学期期末

数学试卷

一、选择题（本大题36分，每小题3分）

1．5的倒数是（　　）

A．﹣5 B．5 C． D．﹣

2．下列计算正确的是（　　）

A．a2+a3＝a5 B．a2•a3＝a6 C．（a2）3＝a5 D．a5÷a3＝a2

3．如图是由5个完全相同的小正方体摆成的几何体，则这个几何体俯视图是（　　）

A． B． C． D．

4．火热的卡塔尔世界杯足球赛已经落下帷幕，最终阿根廷队捧起了大力神杯．据统计，本届世界杯，卡塔尔官方共投入约220000000000美元用于场馆、交通、酒店等基础设施建设，220 000 000 000这个数用科学记数法表示为（　　）

A．22×108 B．220×109 C．2.2×1010 D．2.2×1011

5．不透明的袋子中装有3个红球和2个白球，这些球除了颜色外都相同，从袋子中随机地摸出1个球，则这个球是红球的概率是（　　）

A． B． C． D．

6．如图，已知直线AB，CD被直线ED所截，AB∥CD，∠1＝140°，则∠D为（　　）

A．40° B．50° C．60° D．70°

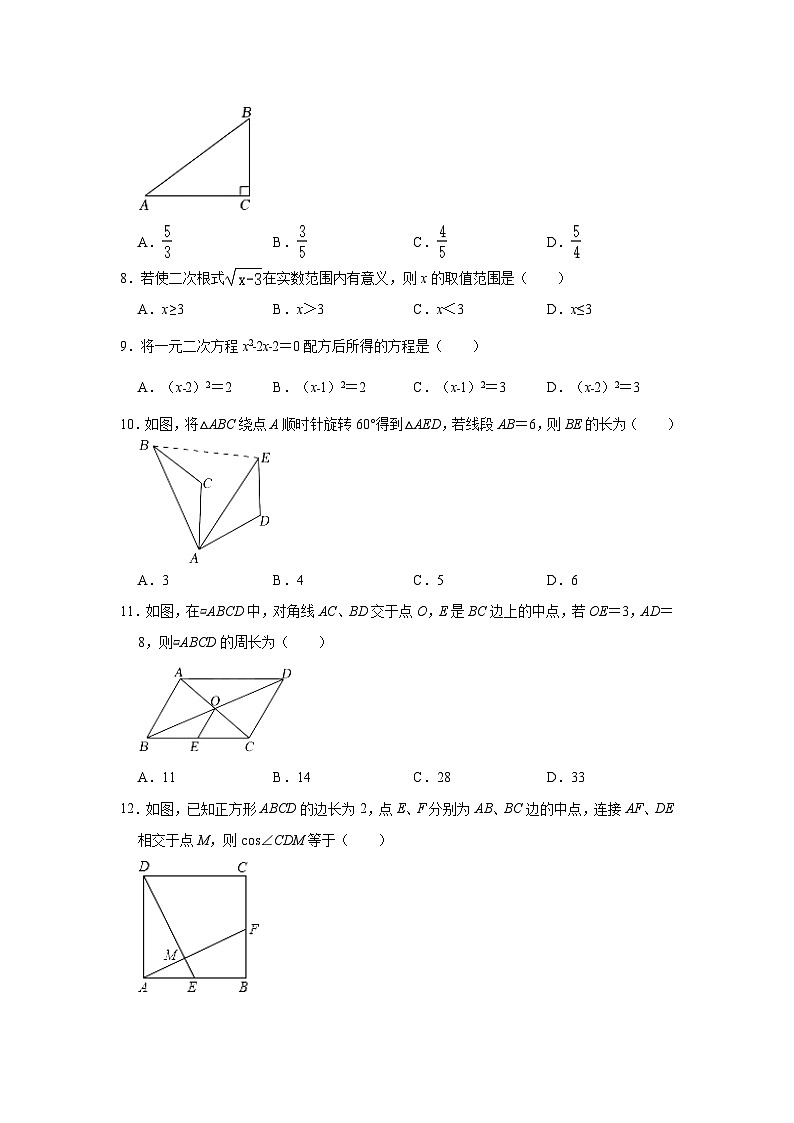
7．如图，在Rt△ABC中，∠ACB＝90°，若AC＝8，BC＝6，则sinA的值为（　　）

A． B． C． D．

8．若使二次根式在实数范围内有意义，则x的取值范围是（　　）

A．x≥3 B．x＞3 C．x＜3 D．x≤3

9．将一元二次方程x2﹣2x﹣2＝0配方后所得的方程是（　　）

A．（x﹣2）2＝2 B．（x﹣1）2＝2 C．（x﹣1）2＝3 D．（x﹣2）2＝3

10．如图，将△ABC绕点A顺时针旋转60°得到△AED，若线段AB＝6，则BE的长为（　　）

A．3 B．4 C．5 D．6

11．如图，在▱ABCD中，对角线AC、BD交于点O，E是BC边上的中点，若OE＝3，AD＝8，则▱ABCD的周长为（　　）

A．11 B．14 C．28 D．33

12．如图，已知正方形ABCD的边长为2，点E、F分别为AB、BC边的中点，连接AF、DE相交于点M，则cos∠CDM等于（　　）

A． B． C． D．

二、填空题（本大题满分12分，每小题3分）

13．因式分解：ax﹣bx＝　   　．

14．已知：，则＝　   　．

15．河堤横断面如图所示，斜坡AB的坡度（即BC：AC），AB＝6m，则BC的长是 　   　．

16．如图，四边形ABCD是平行四边形，以点B为圆心，BC的长为半径作弧交AD于点E，分别以点C、E为圆心，大于的长为半径作弧，两弧交于点P，作射线BP交AD的延长线于点F，∠CBE＝60°，BC＝4，则EF＝　   　．

三、解答题（本大题满分72分）

17．（1）计算：；

（2）解不等式组：．

18．某学校是乒乓球体育传统项目学校，为进一步推动该项目的开展，学校准备到体育用品店购买直拍球拍和横拍球拍若干副，乒乓球赠送．若购买10副直拍球拍和5副横拍球拍花费3250元；购买10副直拍球拍比购买5副横拍球拍多花费750元．求两种球拍每副各多少元？

19．学校开展“书香校园”活动以来，受到同学们的广泛关注，学校为了解全校学生课外阅读的情况，随机调查了部分学生在一周内借阅图书的次数，并制成如图不完整的统计表．

学生借阅图书的次数统计表

请你根据统计图表中的信息，解答下列问题：

（1）本次共随机调查了 　   　名学生；

（2）在该调查中，学生在一周内借阅图书的次数的众数是 　   　次，中位数是 　   　次；

（3）请计算扇形统计图中“3次”所对应扇形的圆心角是 　   　度；

（4）若该校共有2000名学生，根据调查结果，估计该校学生在一周内借阅图书“4次及以上”的有 　   　人．

20．为了维护国家主权和海洋权力，海监部门对我国领海进行常态化巡航．如图所示，正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行，在A处测得灯塔P在北偏东60°方向上，继续航行30分钟后到达B处，此时测得灯塔P在北偏东45°方向上．

（1）AB＝　   　海里；∠APB＝　   　度；

（2）已知在灯塔P的周围35海里内有暗礁，问海监船继续向正东方向航行是否安全？请说明理由．（参考数据：≈1.41，≈1.73）

21．如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．

（1）求证：△BAF≌△DEF；

（2）如图2，过点D作DG∥BE，交BC于点G，连接FG交BD于点O．

①判断四边形BFDG的形状，并说明理由；

②若AB＝6，AD＝8，求FG的长．

22．如图，点A（1，6）和B（n，2）是一次函数y1＝kx+b的图象与反比例函数的图象的两个交点．

（1）求m、n的值；

（2）求一次函数的表达式；

（3）设点P是y轴上的一个动点，当△PAB的周长最小时，求点P的坐标；

（4）在（3）的条件下，设点D是坐标平面内一个动点，当以点A、B、P、D为顶点的四边形是平行四边形时，请直接写出符合条件的所有点D的坐标．

参考答案

一、选择题（本大题36分，每小题3分）

1．解：∵5×＝1，

∴5的倒数是．

故选：C．

2．解：A、a2与a3不是同类项，不能合并，错误；

B、a2•a3＝a5，错误；

C、（a2）3＝a6，错误；

D、a5÷a3＝a2，正确．

故选：D．

3．解：俯视图如选项B所示，

故选：B．

4．解：220000000000＝2.2×1011．

故选：D．

5．解：从袋子中随机地摸出1个球，则这个球是红球的概率是，

故选：B．

6．解：如图，

∵AB∥CD，

∴∠2＝∠D，

∵∠1＝140°，

∴∠D＝∠2＝180°﹣∠1＝180°﹣140°＝40°，

故选：A．

7．解：在△ABC中，∠ACB＝90°，AC＝8，BC＝6，

∴AB＝＝＝10，

∴sinA＝＝＝．

故选：B．

8．解：∵二次根式在实数范围内有意义，

∴x﹣3≥0，解得x≥3．

故选：A．

9．解：∵x2﹣2x﹣2＝0，

∴x2﹣2x＝2，

∴x2﹣2x+1＝2+1，

∴（x﹣1）2＝3．

故选：C．

10．解：∵△ABC绕点A顺时针旋转60°得到△AED，

∴AB＝AE，∠BAE＝60°，

∴△AEB是等边三角形，

∴BE＝AB，

∵AB＝6，

∴BE＝6．

故选：D．

11．解：∵四边形ABCD是平行四边形，

∴OA＝OC＝AC，OB＝OD＝BD，

∵E是BC边上的中点，

∴OE是△ABC的中位线，

∴AB＝2OE＝6，

∵AD＝8，

∴▱ABCD的周长＝2×（6+8）＝28，

故选：C．

12．解：∵E是AB的中点，AB＝2，

∴AE＝AB＝1，

Rt△DAE中，由勾股定理得：DE＝＝＝，

∴cos∠AED＝＝＝，

∵CD∥AB，

∴∠CDM＝∠AED，

∴cos∠CDM＝；

故选：A．

二、填空题（本大题满分12分，每小题3分）

13．解：原式＝x（a﹣b）．

故答案为：x（a﹣b）．

14．解：∵，

∴＝．

15．解：设BC＝xm，

∵斜坡AB的坡度i＝1：，

∴AC＝xm，

由勾股定理得：AC2+BC2＝AB2，即（x）2+x2＝62，

解得：x＝3，

则BC＝3m，

故答案为：3m．

16．解：由尺规作图知BE＝BC＝4，BF平分∠CBE，

∴∠CBF＝∠EBF＝，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠F＝∠CBF，

∴∠F＝∠EBF＝30°，

∴BE＝FE＝4，

故答案为：4．

三、解答题（本大题满分72分）

17．解：（1）原式＝2﹣8×+1

＝2﹣4+1

＝﹣1；

（2），

解①得：x＞1，

解②得：x≤2，

故不等式组的解集为：1＜x≤2．

18．解：设直拍球拍每副x元，横拍球每副y元，由题意得，

，

解得：，

答：直拍球拍每副200元，横拍球每副250元．

19．解：（1）∵被调查的总人数为13÷26%＝50人，

故答案为：50；

（2）由于共有50个数据，其中位数为第25、26个数据的平均数，

而第25、26个数据均为2次，

所以中位数为2次，

出现次数最多的是2次，

所以众数为2次，

故答案为：2、2；

（3）扇形统计图中“3次”所对应扇形的圆心角的度数为360°×20%＝72°；

故答案为：72；

（4）估计该校学生在一周内借阅图书“4次及以上”的人数为2000×＝120人．

故答案为：120．

20．解：（1）AB＝60×＝30（海里）；

由题意得，∠PAB＝90°﹣60°＝30°，∠ABP＝90°+45°＝135°，

∴∠APB＝180°﹣∠PAB﹣∠ABP＝180°﹣30°﹣135°＝15°；

故答案为：30，15；

（2）海监船继续向正东方向航行安全，理由如下：

作PH⊥AB于H，如图：

则△PBH是等腰直角三角形，

∴BH＝PH，

设BH＝PH＝x海里，

由题意得：AB＝60×＝30（海里），

在Rt△APH中，tan∠PAB＝tan30°＝＝，

即 ＝，

解得：x＝15+15≈40.98＞35，

∴海监船继续向正东方向航行安全．

21．（1）证明：如图1，根据折叠，∠E＝∠C＝90°，DC＝DE，

∵四边形ABCD是矩形，

∴AB＝CD，∠A＝90°，

∴AB＝DE，∠A＝∠E，

在△BAF和△DEF中，

，

∴△BAF≌△DEF（ASA）；

（2）解：①结论：四边形BFDG是菱形．

理由：∵四边形ABCD是矩形，

∴AD∥BC，

∴FD∥BG，

又∵DG∥BE，

∴四边形BFDG是平行四边形，

∵DF＝BF，

∴四边形BFDG是菱形；

解：②∵AB＝6，AD＝8，

∴BD＝10．

∴OB＝BD＝5．

假设DF＝BF＝x，∴AF＝AD﹣DF＝8﹣x．

∴在直角△ABF中，AB2+AF2＝BF2，即62+（8﹣x）2＝x2，

解得x＝，

即BF＝，

∴FO＝＝，

∴FG＝2FO＝．

22．解：（1）将点A的坐标代入反比例函数表达式得：6＝，

解得m＝6，

故反比例函数表达式为y＝，

当y＝＝2时，x＝3＝n，即点B的坐标为（3，2），

即m＝6，n＝3；

（2）将点A、B坐标代入一次函数表达式得：

，解得：，

故一次函数表达式为y＝﹣2x+8；

（3）作点A关于y轴的对称点G（﹣1，6），连接BG交y轴于点P，则点P为所求点，

理由：△PAB的周长＝AP+PB+AB＝GP+PB+AB＝BG+AB为最小，

由点B、G的坐标，同理可得：BG的表达式为y＝﹣x+5，

故点P的坐标为（0，5）；

（4）能，理由：

A：由（1）（2）知，点A、B、P的坐标分别为（1，6）、（3，2）、（0，5），

设点D的坐标为（s，t），

①当AB是边时，

则点A向右平移2个单位向下平移4个单位得到B，同样点P（D）向右平移2个单位向下平移4个单位得到D（P），

则0+2＝s，5﹣4＝t或0﹣2＝s，5+4＝t，

解得；

②当AB是对角线时，

由中点公式得：（1+3）＝（s+0），（6+2）＝（5+t），

解得；

故点D的坐标为（2，1）或（﹣2，9）或（4，3）．