河北省邯郸市临漳县2022-2023学年八年级下学期期末教学质量检测数学试卷(含解析)

这是一份河北省邯郸市临漳县2022-2023学年八年级下学期期末教学质量检测数学试卷(含解析)，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
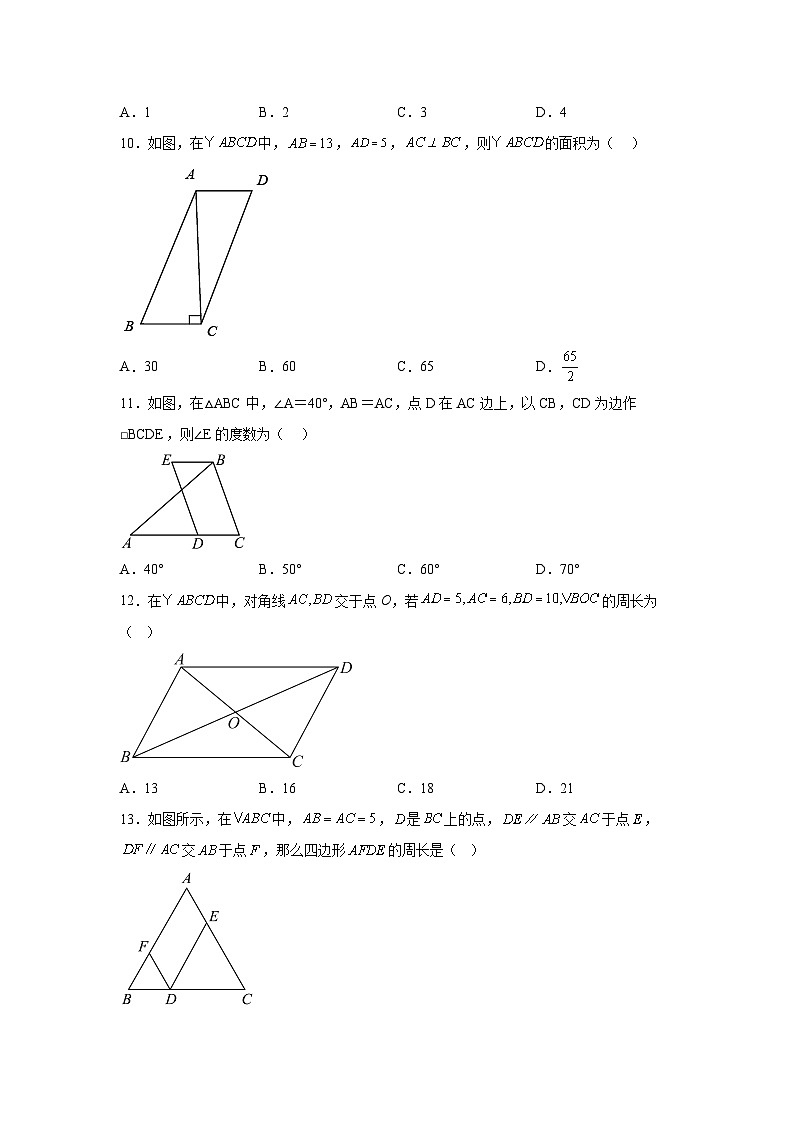
; 2022—2023学年第二学期期末教学质量检测八年级数学试卷一、选择题（每题3分，共48分）1．下列各式由左边到右边的变形中，是因式分解的是（    ）A． B．C． D．2．将提公因式后，另一个因式是（      ）A． B． C． D．3．将多项式因式分解，结果为（   ）A． B． C． D．4．已知甲、乙、丙均为含x的整式，且其一次项的系数皆为正整数．若甲与乙相乘的积为，乙与丙相乘的积为，则甲与丙相乘的积为（    ）A． B． C． D．5．多项式加上一个数或单项式后，使它成为一个多项式的完全平方，那么加上的数或单项式可以从①，②，③，④，⑤中选取，则选取的是（   ）A．① B．③ C．②③⑤ D．①②③④⑤6．若，则x应满足的条件是（   ）A． B． C．且 D．或7．若÷（　　）=，则（　　）中式子为（　　）A．﹣3 B．3﹣2x C．2x﹣3 D．8．计算的结果是（   ）A． B． C． D．a+b9．已知关于x的分式方程的解为，则常数a的值为（   ）A．1 B．2 C．3 D．410．如图，在中，，，，则的面积为（    ）A．30 B．60 C．65 D．11．如图，在△ABC中，∠A＝40°，AB＝AC，点D在AC边上，以CB，CD为边作□BCDE，则∠E的度数为（    ）  A．40° B．50° C．60° D．70°12．在中，对角线交于点O，若的周长为（   ）  A．13 B．16 C．18 D．2113．如图所示，在中，，是上的点，交于点，交于点，那么四边形的周长是（   ）  A．5 B．10 C．15 D．2014．已知，在△ABC中，，如图，（1）分别以B，C为圆心，BC长为半径作弧，两弧交于点D； （2）作射线AD，连接BD，CD．根据以上作图过程及所作图形，下列结论中错误的是（  ）A． B．△BCD是等边三角形C．AD垂直平分BC D．15．小明要从甲地到乙地，两地相距1.8千米．已知他步行的平均速度为90米/分，跑步的平均速度为210米/分，若他要在不超过15分钟的时间内从甲地到达乙地，至少需要跑步多少分钟？设他需要跑步x分钟，则列出的不等式为（　　）A．210x+90（15﹣x）≥1800 B．90x+210（15﹣x）≤1800C．210x+90（15﹣x）≥1.8 D．90x+210（15﹣x）≤1.816．如图，边长为的正方形纸片剪出一个边长为的正方形之后，剩余部分可剪拼成一个长方形，若拼成的长方形一边长为，则另一边长为A． B． C． D．二、填空题（每题3分，共9分）17．如图，在四边形ABCD中，对角线AC、BD交于点O，AD∥BC，请添加一个条件：      ，使四边形ABCD为平行四边形（不添加任何辅助线）．18．如图，在平面直角坐标系中，，，将线段AB先向上平移2个单位长度，再向右平移3个单位长度，得到线段DC，点A与点D为对应点．点P为y轴上一点，且，则满足要求的点P坐标为      ．19．观察填空：如图，各块图形面积之和为，因式分解      ．  三、解答题（63分）20．如图，在中，，，连接，，，．求证：四边形是平行四边形．21．（1）已知，，求的值．（2）解分式方程．22．在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题：（1）①作出△ABC向左平移4个单位长度后得到的△A1B1C1， 并写出点C1的坐标；②作出△ABC关于原点O对称的△A2B2C2， 并写出点C2的坐标；    （2）已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为（－4，－2），请直接写出直线l的函数解析式.23．如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3（1）求证：BN=DN；（2）求△ABC的周长．24．某社区拟建，两类摊位以搞活“地摊经济”，每个类摊位的占地面积比每个类摊位的占地面积多2平方米，建类摊位每平方米的费用为40元，建类摊位每平方米的费用为30元，用60平方米建类摊位的个数恰好是用同样面积建类摊位个数的．（1）求每个，类摊位占地面积各为多少平方米？（2）该社拟建，两类摊位共90个，且类摊位的数量不少于类摊位数量的3倍.求建造这90个摊位的最大费用．25．（1）【模型建立】如图1，等腰直角三角形ABC中，∠ACB=90°，CB=CA，直线ED经过点C，过A作AD⊥ED与D，过B作BE⊥ED于E，求证：△BEC≌△CDA；（2）【模型应用】：已知直线与y轴交于A点，与x轴交于B点，将线段AB绕点B逆时针旋转90度，得到线段BC，过点A，C作直线，求直线AC的解析式；   26．如图，等边△ABC的边长为8，动点M从点B出发，沿B→A→C→B的方向以每秒3个单位长度的速度运动，动点N从点C出发，沿C→A→B－C的方向以每秒2个单位长度的速度运动.（1）若动点M、N同时出发，经过几秒第一次相遇？（2）若动点M、N同时出发，且其中一点到达终点时，另一点即停止运动．在△ABC的边上是否存在一点D，使得以点A、M、N、D为顶点的四边形为平行四边形？若存在，求此时运动的时间及点D的具体位置；若不存在，请说明理由.     
答案1．B解析：解：A右边不是几个整式的积的形式，不是因式分解，故本选项不符合题意；B．是因式分解，故本选项符合题意；C．右边不是几个整式的积的形式，不是因式分解，故本选项不符合题意；D．右边不是几个整式的积的形式，不是因式分解，故本选项不符合题意；故选：B．2．A解析：解：故选：A3．C解析：解：，故选：C．4．B解析：解：甲与乙相乘的积为，乙与丙相乘的积为，甲为，乙为，丙为，则甲与丙相乘的积为，故选：B．5．C解析：解：当和1是两个平方项时：∵，∴乘积二倍项为，或；当是乘积二倍项，1为平方项时：∵，∴另一个平方项为，综上：加上的数或单项式可以选取的是，，；即可以选取的是②③⑤，故选：C．6．C解析：解：当时，分子与分母同时除以，分式的值不变，即，，又分式的分母不能为0，，x应满足的条件是且，故选C．7．B解析：∵÷（　　）=，∴÷×（x﹣1）=3﹣2x．∴（　　）中式子为：3﹣2x．故选：B．8．C解析：解：原式，，故选：C．9．C解析：解：将代入方程得：即：解得：故选：C10．B解析：解：四边形是平行四边形，，，，，则的面积为，故选：B．11．D解析：解：∵∠A＝40°，AB＝AC，∴∠ABC=∠C=70°，∵四边形ABCD是平行四边形，∴∠E=∠C=70°．故选：D．12．A解析：解：∵四边形是平行四边形，对角线交于点O，∴，∴的周长为，故选：A．13．B解析：解：，，则四边形是平行四边形，，，，，，，所以：的周长等于．故选：B．14．D解析：解：∵∴△BCD是等边三角形故选项B正确；∵，∴∴故选项A正确；∵，∴据三线合一得出AD垂直平分BC故选项C正确；∵四边形ABCD的面积等于的面积与的面积之和∴故选项D错误．故选：D．15．A解析：解：由题意可得210x+90（15﹣x）≥1800，故选：A．16．B解析：依题意得剩余部分为：(2m+3)2−(m+3)2=4m2+12m+9−m2−6m−9=3m2+6m，而拼成的矩形一边长为m，∴另一边长是(3m2+6m)÷m=3m+6.故答案选：B.17．AD=BC．解析：当AD∥BC，AD=BC时，四边形ABCD为平行四边形．故答案是AD=BC（答案不唯一）．18．或##或解析：解：由题意可知，经过平移后，，∴到轴的距离为，记为，到轴的距离为，记为，∴，，，，∵为轴上的一点，记点到轴的距离为，∴，，∴，∴点的纵坐标为，∴点的坐标为或．故答案为：或19．解析：解：根据题意可得：各块图形面积之和为，根据长方形面积公式可得，整个图形面积为，∴，故答案为：．20．见解析解析：证明：∵四边形ABCD是平行四边形，∴∠A=∠C，∠B=∠D，AD=BC，又∵BF=DH，∴CF=AH，在△AEH和△CGF中，，∴△AEH≌△CGF（SAS），∴EH=GF；同理：GH=EF；∴四边形EFGH是平行四边形．21．（1）10；（2）无实数根解析：解：（1），当，时，原式；（2），去分母，得：，去括号，合并同类项，得：，解得：，检验：当时，，因此是原方程的增根，∴该分式方程无实数根．22．(1)作图见解析，C1的坐标C1（-1,2）, C2的坐标C2（-3,-2）；（2）y=-x.  解析：（1）如图所示， C1的坐标C1（-1,2）, C2的坐标C2（-3,-2）（2）解：∵A（2,4），A3（-4，-2），∴直线l的函数解析式：y=-x.  23．（1）见解析，（2）41解析：（1）证明：∵BN⊥AN于点N，∴，在△ABN和△ADN中，∵， ∴△ABN≌△ADN（ASA）．∴BN=DN．（2）∵△ABN≌△ADN，∴AD=AB=10，DN=NB．又∵点M是BC中点，∴MN是△BDC的中位线．∴CD=2MN=6．∴△ABC的周长=AB+BC+CD+AD=10+15+6+10=41．24．（1）5平方米；3平方米  （2）10520元解析：解：（1）设每个类摊位占地面积平方米，则类占地面积平方米由题意得解得，∴，经检验为分式方程的解∴每个类摊位占地面积5平方米，类占地面积3平方米（2）设建类摊位个，则类个，费用为∵∴，∵110>0，∴z随着a的增大而增大，又∵a为整数，∴当时z有最大值，此时∴建造90个摊位的最大费用为10520元25．（1）证明见解析；（2）y=x+3解析：证明：（1）∵AD⊥ED， BE⊥ED∴∠E=∠D=90°又∵∠ACB=90°，∴∠EBC+∠BCE=∠BCE+∠ACD=90°，∴∠EBC=∠ACD，在△BEC和△CDA中， ∴△BEC≌△CDA（AAS）；  （2）如图，过C作CD⊥x轴于点D，  直线与y轴交于A点，与x轴交于B点，令y=0可求得x=-4，令x=0可求得y=3，∴OA=3，OB=4，同（1）可证得△CDB≌△BAO，∴CD=BO=4，BD=AO=3，∴OD=4+3=7，∴C（-7，4），且A（0，3），设直线AC解析式为y=kx+3，把C点坐标代入可得4=-7k+3，解得k=∴直线AC解析式为y=x+326．（1）经过t=s第一次相遇.    （2）运动了或s时，A、M、N、D四点能够成平行四边形，此时点D在BC上，且BD=或．解析：（1）由题意得：3t+2t=16，解得：t=；答：若动点M、N同时出发，经过t=s第一次相遇.（2）①当0≤t≤时，点M、N、D的位置如图2所示：  ∵四边形ANDM为平行四边形，∴DM=AN，DM∥AN．∴∠MDB=∠C=60°∵△ABC为等边三角形，∴∠B=∠C=60°．∴∠MDB =∠B．∴MB=MD= AN∴AN+CN=MB+CN=8，即：3t+2t=8，t=，此时点D在BC上，且BD=（或CD=），②当＜t≤4时，此时A、M、N三点在同一直线上，不能构成平行四边形；③4＜t≤时，点M、N、D的位置如图所1示：  ∵四边形ANDM为平行四边形，∴DN=AM，AM∥DN．∴∠NDB=∠C=60°∵△ABC为等边三角形，∴∠B=∠C =60°．∴∠NDB=∠B．∴BN=ND= AM．∴AN+NB=AN+AM=8，2t-8+3t-8=8，解得：t=，此时点D在BC上，且BD=（或CD=），④当＜t≤8时，点M、N、D的位置如图所3示：  则BN=16-2t，BM=24-3t，∵△ABC为等边三角形，∴∠A=∠C=60°．若MN∥AC,则∠BNM=∠A=60°, ∠BMN=∠C=60°∴△BNM为等边三角形，∴BN=BM，即：16-2t =24-3t，解得t=8，此时M、N重合，不能构成平行四边形．答：运动了或s时，A、M、N、D四点能够成平行四边形，此时点D在BC上，且BD=或．