

山东省东营市2021-2023三年中考数学真题分类汇编-02填空题知识点分类(含答案)
展开
这是一份山东省东营市2021-2023三年中考数学真题分类汇编-02填空题知识点分类(含答案),共23页。试卷主要包含了因式分解等内容,欢迎下载使用。
山东省东营市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
一.科学记数法—表示较大的数(共2小题)
1.(2022•东营)2022年2月20日,北京冬奥会圆满落幕,赛事获得了数十亿次数字平台互动,在中国仅电视收视人数就超6亿.6亿用科学记数法表示为 .
2.(2021•东营)2021年5月11日,第七次全国人口普查数据显示,全国人口比第六次全国人口普查数据增加了7206万人.7206万用科学记数法表示 .
二.科学记数法与有效数字(共1小题)
3.(2023•东营)我国古代数学家祖冲之推算出π的近似值为,它与π的误差小于0.0000003.0.0000003用科学记数法表示为 .
三.提公因式法与公式法的综合运用(共3小题)
4.(2023•东营)因式分解:3ma2﹣6mab+3mb2= .
5.(2022•东营)因式分解:x3﹣9x= .
6.(2021•东营)因式分解:4a2b﹣4ab+b= .
四.根的判别式(共1小题)
7.(2022•东营)关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则k的取值范围是 .
五.由实际问题抽象出分式方程(共1小题)
8.(2021•东营)某地积极响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展荒山绿化,打造美好家园,促进旅游发展.某工程队承接了90万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了任务.设原计划每天绿化的面积为x万平方米,则所列方程为 .
六.解一元一次不等式组(共1小题)
9.(2021•东营)不等式组的解集为 .
七.点的坐标(共1小题)
10.(2023•东营)如图,一束光线从点A(﹣2,5)出发,经过y轴上的点B(0,1)反射后经过点C(m,n),则2m﹣n的值是 .
八.规律型:点的坐标(共1小题)
11.(2023•东营)如图,在平面直角坐标系中,直线l:y=x﹣与x轴交于点A1,以OA1为边作正方形A1B1C1O,点C1在y轴上,延长C1B1交直线l于点A2,以C1A2为边作正方形A2B2C2C1,点C2在y轴上,以同样的方式依次作正方形A3B3C3C2,⋯,正方形A2023B2023C2023C2022,则点B2023的横坐标是 .
九.一次函数图象上点的坐标特征(共1小题)
12.(2022•东营)如图,△AB1A1,△A1B2A2,△A2B3A3,…是等边三角形,直线y=x+2经过它们的顶点A,A1,A2,A3,…,点B1,B2,B3,…在x轴上,则点A2022的横坐标是 .
一十.反比例函数系数k的几何意义(共1小题)
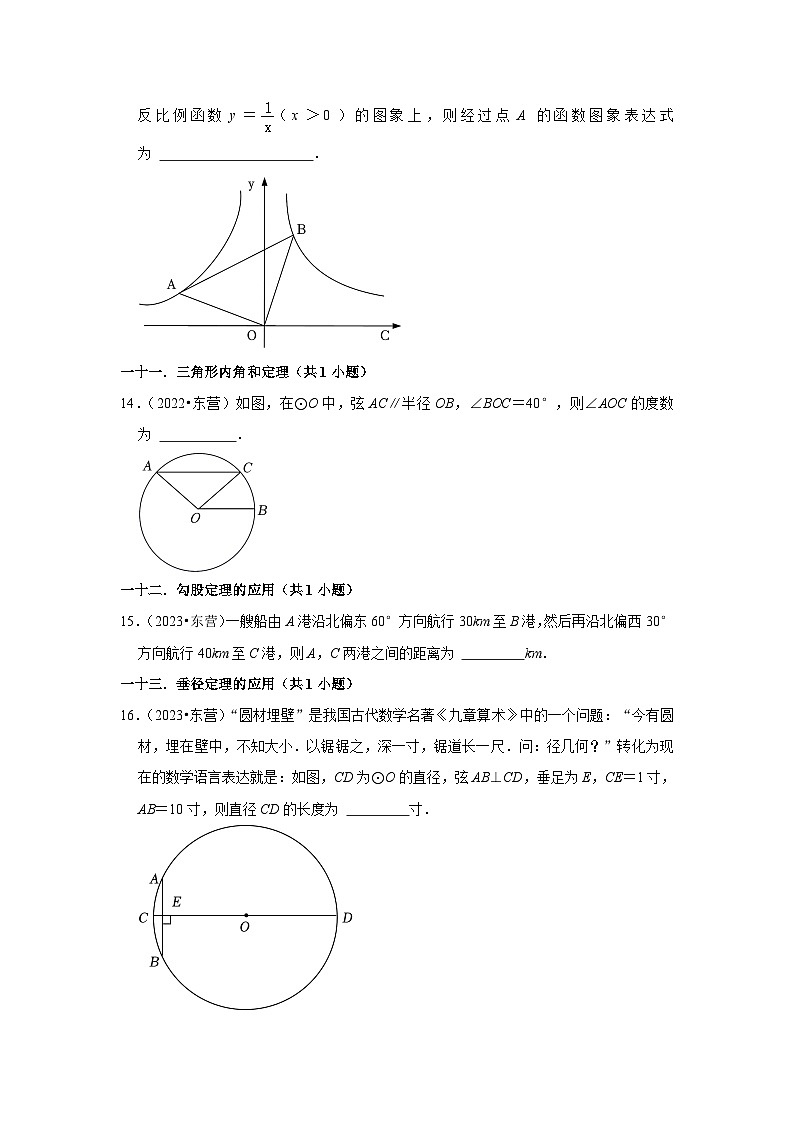
13.(2022•东营)如图,△OAB是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数y=(x>0)的图象上,则经过点A的函数图象表达式为 .
一十一.三角形内角和定理(共1小题)
14.(2022•东营)如图,在⊙O中,弦AC∥半径OB,∠BOC=40°,则∠AOC的度数为 .
一十二.勾股定理的应用(共1小题)
15.(2023•东营)一艘船由A港沿北偏东60°方向航行30km至B港,然后再沿北偏西30°方向航行40km至C港,则A,C两港之间的距离为 km.
一十三.垂径定理的应用(共1小题)
16.(2023•东营)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何?”转化为现在的数学语言表达就是:如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长度为 寸.
一十四.扇形面积的计算(共1小题)
17.(2021•东营)如图,在▱ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F,若∠BAC=60°,∠ABC=100°,BC=4,则扇形BEF的面积为 .
一十五.作图—基本作图(共1小题)
18.(2023•东营)如图,在△ABC中,以点C为圆心,任意长为半径作弧,分别交AC,BC于点D,E;分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于点F;作射线CF交AB于点G.若AC=9,BC=6,△BCG的面积为8,则△ACG的面积为 .
一十六.翻折变换(折叠问题)(共1小题)
19.(2021•东营)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为 .
一十七.相似三角形的判定与性质(共2小题)
20.(2022•东营)如图,在△ABC中,点F、G在BC上,点E、H分别在AB、AC上,四边形EFGH是矩形,EH=2EF,AD是△ABC的高,BC=8,AD=6,那么EH的长为 .
21.(2021•东营)如图,正方形ABCB1中,AB=,AB与直线l所夹锐角为60°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…,依此规律,则线段A2020A2021= .
一十八.条形统计图(共1小题)
22.(2021•东营)如图所示是某校初中数学兴趣小组年龄结构条形统计图,该小组年龄最小为11岁,最大为15岁,根据统计图所提供的数据,该小组组员年龄的中位数为 岁.
一十九.众数(共1小题)
23.(2022•东营)为了落实“双减”政策,东营市某学校对初中学生的课外作业时长进行了问卷调查,15名同学的作业时长统计如下表,则这组数据的众数是 分钟.
作业时长(单位:分钟)
50
60
70
80
90
人数(单位:人)
1
4
6
2
2
二十.方差(共1小题)
24.(2023•东营)为备战东营市第十二届运动会,某县区对甲、乙、丙、丁四名射击运动员进行射击测试,他们射击测试成绩的平均数(单位:环)及方差S2(单位:环2)如表所示:
甲
乙
丙
丁
9.6
8.9
9.6
9.6
S2
1.4
0.8
2.3
0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择 .
山东省东营市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
参考答案与试题解析
一.科学记数法—表示较大的数(共2小题)
1.(2022•东营)2022年2月20日,北京冬奥会圆满落幕,赛事获得了数十亿次数字平台互动,在中国仅电视收视人数就超6亿.6亿用科学记数法表示为 6×108 .
【答案】6×108.
【解答】解:6亿=600000000=6×108.
故答案为:6×108.
2.(2021•东营)2021年5月11日,第七次全国人口普查数据显示,全国人口比第六次全国人口普查数据增加了7206万人.7206万用科学记数法表示 7.206×107 .
【答案】7.206×107.
【解答】解:7206万=72060000=7.206×107,
故答案为:7.206×107.
二.科学记数法与有效数字(共1小题)
3.(2023•东营)我国古代数学家祖冲之推算出π的近似值为,它与π的误差小于0.0000003.0.0000003用科学记数法表示为 3×10﹣7 .
【答案】3×10﹣7.
【解答】解:0.0000003=3×10﹣7,
故答案为:3×10﹣7.
三.提公因式法与公式法的综合运用(共3小题)
4.(2023•东营)因式分解:3ma2﹣6mab+3mb2= 3m(a﹣b)2 .
【答案】3m(a﹣b)2.
【解答】解:3ma2﹣6mab+3mb2
=3m(a2﹣2ab+b2)
=3m(a﹣b)2,
故答案为:3m(a﹣b)2.
5.(2022•东营)因式分解:x3﹣9x= x(x+3)(x﹣3) .
【答案】见试题解答内容
【解答】解:x3﹣9x,
=x(x2﹣9),
=x(x+3)(x﹣3).
6.(2021•东营)因式分解:4a2b﹣4ab+b= b(2a﹣1)2 .
【答案】见试题解答内容
【解答】解:原式=b(4a2﹣4a+1)
=b(2a﹣1)2.
故答案为:b(2a﹣1)2.
四.根的判别式(共1小题)
7.(2022•东营)关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则k的取值范围是 k<2且k≠1 .
【答案】k<2且k≠1.
【解答】解:根据题意得k﹣1≠0且Δ=(﹣2)2﹣4×(k﹣1)>0,
解得k<2且k≠1,
所以k的取值范围是k<2且k≠1.
故答案为:k<2且k≠1.
五.由实际问题抽象出分式方程(共1小题)
8.(2021•东营)某地积极响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展荒山绿化,打造美好家园,促进旅游发展.某工程队承接了90万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了任务.设原计划每天绿化的面积为x万平方米,则所列方程为 ﹣=30 .
【答案】﹣=30.
【解答】解:设原计划每天绿化的面积为x万平方米,则实际每天绿化的面积为(1+25%)x万平方米,
依题意得:﹣=30.
故答案为:﹣=30.
六.解一元一次不等式组(共1小题)
9.(2021•东营)不等式组的解集为 ﹣1≤x<2 .
【答案】见试题解答内容
【解答】解:解不等式﹣≤1,得:x≥﹣1,
解不等式5x﹣1<3(x+1),得:x<2,
则不等式组的解集为﹣1≤x<2,
故答案为:﹣1≤x<2.
七.点的坐标(共1小题)
10.(2023•东营)如图,一束光线从点A(﹣2,5)出发,经过y轴上的点B(0,1)反射后经过点C(m,n),则2m﹣n的值是 ﹣1 .
【答案】﹣1.
【解答】解:∵点A(﹣2,5)关于y轴的对称点为A′(2,5),
∴反射光线所在直线过点B(0,1)和A′(2,5),
设A'B的解析式为:y=kx+1,过点A′(2,5),
∴5=2k+1,
∴k=2,
∴A'B的解析式为:y=2x+1,
∵反射后经过点C(m,n),
∴2m+1=n,
∴2m﹣n=﹣1.
故答案为:﹣1.
八.规律型:点的坐标(共1小题)
11.(2023•东营)如图,在平面直角坐标系中,直线l:y=x﹣与x轴交于点A1,以OA1为边作正方形A1B1C1O,点C1在y轴上,延长C1B1交直线l于点A2,以C1A2为边作正方形A2B2C2C1,点C2在y轴上,以同样的方式依次作正方形A3B3C3C2,⋯,正方形A2023B2023C2023C2022,则点B2023的横坐标是 (1+)2022 .
【答案】(1+)2022.
【解答】解:当y=0时,有x﹣1=0,
解得:x=1,
∴点A1的坐标为(1,0).
∵四边形A1B1C1O为正方形,
∴OA1=A1B1=OC1=1,
∴点B1(1,1),
B1的横坐标为1;
∴y=1时,1=x﹣,
解得:x=,
∴点A2的坐标为(,1),
A2B2C2C1是正方形,
∴A2B2=C2C1=A2C1=,
∴点B2(,2+),
即B2的横坐标为;
当y=2+时,2+=x﹣,
解得:x=(),
∴点A3((),2+),
∵A3B3C3C2是正方形,
∴A3B3=C3C2=A3C2=(),
∴点B3的横坐标为()=(1+)2,
……,
以此类推,则点B2023的横坐标是(1+)2022.
故答案为:(1+)2022.
九.一次函数图象上点的坐标特征(共1小题)
12.(2022•东营)如图,△AB1A1,△A1B2A2,△A2B3A3,…是等边三角形,直线y=x+2经过它们的顶点A,A1,A2,A3,…,点B1,B2,B3,…在x轴上,则点A2022的横坐标是 (22023﹣2) .
【答案】(22023﹣2).
【解答】解:如图:
∵直线y=x+2,令x=0,则y=2,
令y=0,则x+2=0,
解得x=﹣2,
∴A(0,2),C(﹣2,0),
∴OA=2,OC=2,
∴∠OCA=30°,
∵△AB1A1,△A1B2A2,△A2B3A3,…是等边三角形,
∴∠AA1B1、∠AA2B2=60°,A1B1=AB1=AC=2OA=4,
……
∴△A1B1C、△A2B2C、……是含30°角的直角三角形,
∴A1B1=4=22,A2B2=8=23,……,
∴OB1=A1B1﹣OC=4=2,OB2=A2B2﹣OC=8=6,
∴A1(2,4),A2(6,8),
……
∴An[(2n+1﹣2),2n+1],
∴点A2022的横坐标是(22023﹣2),
故答案为:(22023﹣2).
一十.反比例函数系数k的几何意义(共1小题)
13.(2022•东营)如图,△OAB是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数y=(x>0)的图象上,则经过点A的函数图象表达式为 y=﹣ .
【答案】y=﹣.
【解答】解:如图,作AD⊥x轴于D,BC⊥x轴于C,
∴∠ADO=∠BCO=90°,
∵∠AOB=90°,
∴∠AOD+∠BOC=90°,
∴∠AOD+∠DAO=90°,
∴∠BOC=∠DAO,
∵OB=OA,
∴△BOC≌△OAD(AAS),
∵点B在反比例函数y=(x>0)的图象上,
∴S△OBC=,
∴S△OAD=,
∴k=﹣1,
∴经过点A的反比例函数解析式为y=﹣.
故答案为:y=﹣.
一十一.三角形内角和定理(共1小题)
14.(2022•东营)如图,在⊙O中,弦AC∥半径OB,∠BOC=40°,则∠AOC的度数为 100° .
【答案】100°.
【解答】解:∵AC∥半径OB,
∴∠OCA=∠BOC=40°,
∵OA=OC,
∴∠A=∠OCA=40°,
∴∠AOC=180°﹣∠A﹣∠OCA=180°﹣40°﹣40°=100°.
故答案为:100°.
一十二.勾股定理的应用(共1小题)
15.(2023•东营)一艘船由A港沿北偏东60°方向航行30km至B港,然后再沿北偏西30°方向航行40km至C港,则A,C两港之间的距离为 50 km.
【答案】50.
【解答】解:如图:
由题意得:∠DAB=60°,∠FBC=30°,AD∥EF,
∴∠DAB=∠ABE=60°,
∴∠ABC=180°﹣∠ABE﹣∠FBC=90°,
在Rt△ABC中,AB=30km,BC=40km,
AC===50(km),
∴A,C两港之间的距离为50km,
故答案为:50.
一十三.垂径定理的应用(共1小题)
16.(2023•东营)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何?”转化为现在的数学语言表达就是:如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长度为 26 寸.
【答案】26.
【解答】解:连接OA,
设⊙O的半径是r寸,
∵直径CD⊥AB,
∴AE=AB=×10=5寸,
∵CE=1寸,
∴OE=(r﹣1)寸,
∵OA2=OE2+AE2,
∴r2=(r﹣1)2+52,
∴r=13,
∴直径CD的长度为2r=26寸.
故答案为:26.
一十四.扇形面积的计算(共1小题)
17.(2021•东营)如图,在▱ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F,若∠BAC=60°,∠ABC=100°,BC=4,则扇形BEF的面积为 .
【答案】.
【解答】解:∵∠BAC=60°,∠ABC=100°,
∴∠ACB=20°,
又∵E为BC的中点,
∴BE=EC=BC=2,
∵BE=EF,
∴EF=EC=2,
∴∠EFC=∠ACB=20°,
∴∠BEF=40°,
∴扇形BEF的面积==,
故答案为:.
一十五.作图—基本作图(共1小题)
18.(2023•东营)如图,在△ABC中,以点C为圆心,任意长为半径作弧,分别交AC,BC于点D,E;分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于点F;作射线CF交AB于点G.若AC=9,BC=6,△BCG的面积为8,则△ACG的面积为 12 .
【答案】12.
【解答】解:如图,过点G作GM⊥AC于点M,GN⊥BC于点N.
由作图可知CG平分∠ACB,
∵GM⊥AC,GN⊥BC,
∴GM=GN,
∵S△BCG=•BC•GN=8,BC=6,
∴GN=,
∴GN=GM=,
∴S△AGC=•AC•GM=×9×=12,
故答案为:12.
一十六.翻折变换(折叠问题)(共1小题)
19.(2021•东营)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为 .
【答案】.
【解答】解:方法一、设CF与DE交于点O,
∵将△CDF沿CF折叠,点D落在点G处,
∴GO=DO,CF⊥DG,
∵四边形ABCD是正方形,
∴AD=CD,∠A=∠ADC=90°=∠FOD,
∴∠CFD+∠FCD=90°=∠CFD+∠ADE,
∴∠ADE=∠FCD,
在△ADE和△DCF中,
,
∴△ADE≌△DCF(ASA),
∴AE=DF=5,
∵AE=5,AD=12,
∴DE===13,
∵cos∠ADE=,
∴,
∴DO==GO,
∴EG=13﹣2×=,
方法二、易证△ADE≌△DCF(ASA),
∴AE=DF=5,
∴DE===13,
∵将△CDF沿CF折叠,点D落在点G处,
∴GO=DO,CF⊥DG,
∵S△DFC=×DF×CD=×CF×DO,
∴DO=,
∴DG=2DO=,
∴EG=13﹣=,
故答案为:.
一十七.相似三角形的判定与性质(共2小题)
20.(2022•东营)如图,在△ABC中,点F、G在BC上,点E、H分别在AB、AC上,四边形EFGH是矩形,EH=2EF,AD是△ABC的高,BC=8,AD=6,那么EH的长为 .
【答案】.
【解答】解:设AD交EH于点R,
∵矩形EFGH的边FG在BC上,
∴EH∥BC,∠EFC=90°,
∴△AEH∽△ABC,
∵AD⊥BC于点D,
∴∠ARE=∠ADB=90°,
∴AR⊥EH,
∴=,
∵EF⊥BC,RD⊥BC,EH=2EF,
∴RD=EF=EH,
∵BC=8,AD=6,AR=6﹣EH,
∴=,
解得EH=,
∴EH的长为,
故答案为:.
21.(2021•东营)如图,正方形ABCB1中,AB=,AB与直线l所夹锐角为60°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…,依此规律,则线段A2020A2021= 2×()2020 .
【答案】2×()2020.
【解答】解:根据题意可知AB1=AB=,∠B1AA1=90°﹣60°=30°,
∴tan∠B1AA1==,
∴A1B1=AB1×=×=1,AA1=2A1B1=2,
A2B2=A1B2×=A1B1×=,A1A2=2A2B2=2×,
A3B3=A2B3×=A2B2×=×=()2,A2A3=2A3B3=2×()2,
∴A2021B2021=A2020B2021×=()2020,A2020A2021=2A2021B2021=2×()2020,
故答案为:2×()2020.
一十八.条形统计图(共1小题)
22.(2021•东营)如图所示是某校初中数学兴趣小组年龄结构条形统计图,该小组年龄最小为11岁,最大为15岁,根据统计图所提供的数据,该小组组员年龄的中位数为 13 岁.
【答案】13.
【解答】解:根据题意排列得:11,11,12,12,12,13,13,13,13,13,14,14,14,14,15,15,15,15,
则该小组组员年龄的中位数为×(13+13)=13(岁),
故答案为:13.
一十九.众数(共1小题)
23.(2022•东营)为了落实“双减”政策,东营市某学校对初中学生的课外作业时长进行了问卷调查,15名同学的作业时长统计如下表,则这组数据的众数是 70 分钟.
作业时长(单位:分钟)
50
60
70
80
90
人数(单位:人)
1
4
6
2
2
【答案】70.
【解答】解:∵70分钟出现了6次,它的次数最多,
∴众数是70分钟.
故答案为:70.
二十.方差(共1小题)
24.(2023•东营)为备战东营市第十二届运动会,某县区对甲、乙、丙、丁四名射击运动员进行射击测试,他们射击测试成绩的平均数(单位:环)及方差S2(单位:环2)如表所示:
甲
乙
丙
丁
9.6
8.9
9.6
9.6
S2
1.4
0.8
2.3
0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择 丁 .
【答案】丁.
【解答】解:由表格知,甲、丙、丁,平均成绩较好,
而丁成绩的方差小,成绩更稳定,
所以要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择丁.
故答案为:丁.
相关试卷
这是一份河南省2021-2023三年中考数学真题分类汇编-02填空题知识点分类,共16页。
这是一份山东省青岛市2021-2023三年中考数学真题分类汇编-02填空题知识点分类,共18页。试卷主要包含了2= ,×= ,之间的反比例函数关系如图所示等内容,欢迎下载使用。
这是一份2021-2023三年浙江省绍兴市中考数学真题分类汇编-02填空题知识点分类(含答案),共18页。试卷主要包含了因式分解,分解因式,方程的解是 等内容,欢迎下载使用。









