
2022-2023学年四川省眉山市北外附属东坡外国语学校九年级(上)入学数学试卷(含解析)
展开2022-2023学年四川省眉山市北外附属东坡外国语学校九年级第一学期入学数学试卷
一、选择题:本大题共8小题,每小题3分,共24分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,矩形ABCD的两对角线相交于点O,若AD=,CD=1,则∠ADB的度数为( )
A.20° B.30° C.45° D.60°
2.若点(m﹣1,2m+1)在第二象限,则m的取值范围为( )
A.m>1 B.m<﹣ C.﹣<m<1 D.m>1或m<﹣
3.如图,在▱ABCD中,∠ADC的平分线交AB边于点E,若CD=5,BE=3,则BC的长为( )
A. B.2 C. D.3
4.已知直线y=kx+b,若k+b=﹣3,kb=2,则该直线不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,在菱形ABCD中,点B在x轴上,点C的坐标为(6,2),点A的坐标为(0,2),则点D的坐标为( )
A.(4,4) B.(3,3) C.(3,4) D.(2,3)
6.已知点(﹣1,a)和点(,b)都在直线y=2x﹣3的图象上,则a,b的大小关系是( )
A.a>b B.a<b
C.a=b D.a,b的大小不能确定
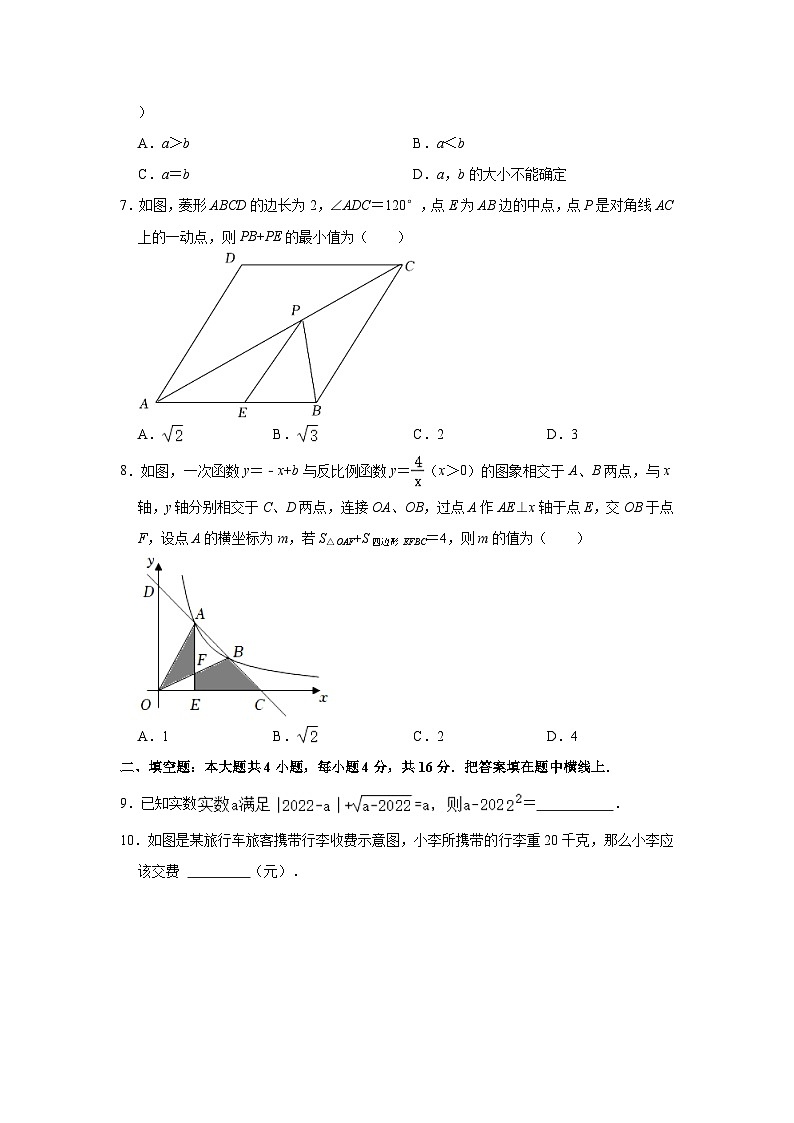
7.如图,菱形ABCD的边长为2,∠ADC=120°,点E为AB边的中点,点P是对角线AC上的一动点,则PB+PE的最小值为( )
A. B. C.2 D.3
8.如图,一次函数y=﹣x+b与反比例函数y=(x>0)的图象相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB,过点A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m,若S△OAF+S四边形EFBC=4,则m的值为( )
A.1 B. C.2 D.4
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
9.已知实数= .
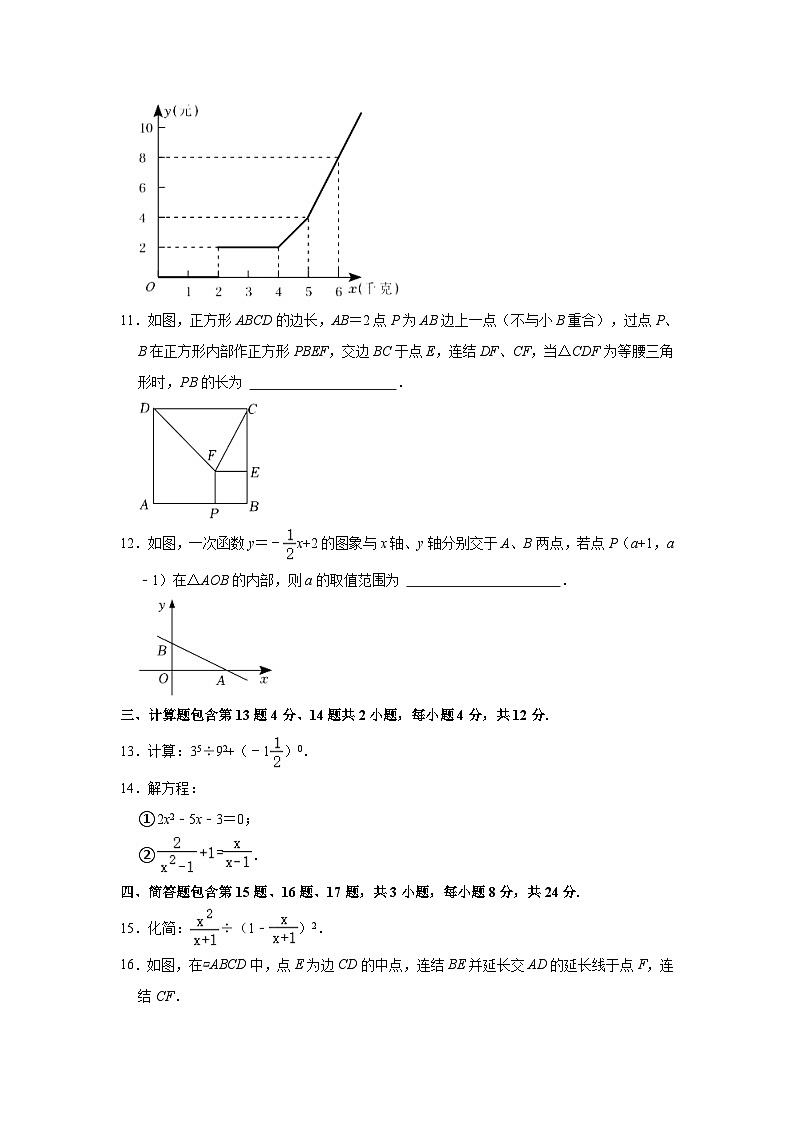
10.如图是某旅行车旅客携带行李收费示意图,小李所携带的行李重20千克,那么小李应该交费 (元).
11.如图,正方形ABCD的边长,AB=2点P为AB边上一点(不与小B重合),过点P、B在正方形内部作正方形PBEF,交边BC于点E,连结DF、CF,当△CDF为等腰三角形时,PB的长为 .
12.如图,一次函数y=﹣x+2的图象与x轴、y轴分别交于A、B两点,若点P(a+1,a﹣1)在△AOB的内部,则a的取值范围为 .
三、计算题包含第13题4分、14题共2小题,每小题4分,共12分.
13.计算:35÷92+(﹣1)0.
14.解方程:
①2x2﹣5x﹣3=0;
②.
四、简答题包含第15题、16题、17题,共3小题,每小题8分,共24分.
15.化简:÷(1﹣)2.
16.如图,在▱ABCD中,点E为边CD的中点,连结BE并延长交AD的延长线于点F,连结CF.
求证:四边形BCFD为平行四边形.
17.如图,点A、B分别在反比例函数和的图象上,线段AB与x轴相交于点P.
(1)如图①,若AB⊥x轴,且|AP|=2|PB|,k1+k2=1.求k1、k2的值;
(2)如图②,若点P是线段AB的中点,且△OAB的面积为2.求k1﹣k2的值.
五、解答题共2小题,第18题12分,第19题12分,共24分.
18.点P为正方形ABCD对角线BD上的一个动点,作射线AP,BF⊥AP于F,DE⊥AP于E,点O为BD中点.
(1)如图1,点P在DO上时,求证:△ADE≌△BAF;
(2)如图2,作射线EO,交BF所在直线于点G,求证:B,G,D,E四点所围成的四边形是平行四边形;
(3)在(2)的条件下,若AB=13,AF=12,求平行四边形BGDE的面积.
19.如图,已知点A(t,1)在第一象限,将OA绕点O顺时针旋转45°得到OB,若反比例数y=(k>0)的图象经过点A、B,求k的值.
参考答案
一、选择题:本大题共8小题,每小题3分,共24分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,矩形ABCD的两对角线相交于点O,若AD=,CD=1,则∠ADB的度数为( )
A.20° B.30° C.45° D.60°
【分析】根据矩形的性质求出AB的长和∠DAB的度数,然后利用tan∠ADB=即可解答.
解:∵四边形ABCD是矩形,
∴∠BAD=90°,AB=CD=1,
在Rt△ABD中,
tan∠ADB==,
∴∠ADB=30°.
故选:B.
【点评】本题考查了矩形的性质以及锐角三角函数,熟记矩形的性质并灵活运用是解题的关键.矩形的性质:①平行四边形的性质矩形都具有; ②角:矩形的四个角都是直角;③边:邻边垂直;④对角线:矩形的对角线相等.
2.若点(m﹣1,2m+1)在第二象限,则m的取值范围为( )
A.m>1 B.m<﹣ C.﹣<m<1 D.m>1或m<﹣
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
解:∵点(m﹣1,2m+1)在第二象限,
∴,
解不等式①,得:m<1,
解不等式②,得:m>﹣,
则不等式组的解集为﹣<m<1.
故选:C.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
3.如图,在▱ABCD中,∠ADC的平分线交AB边于点E,若CD=5,BE=3,则BC的长为( )
A. B.2 C. D.3
【分析】由平行四边形的性质可得AB∥CD,AB=CD=5,可求得AE的长,利用平行线的性质及角平分线的定义可得∠ADE=∠AED,进而可求得AD=AE,即可求解
解:∵四边形ABCD为平行四边形,
∴AB=CD=5,AB∥CD,AD=BC,
∴AE=AB﹣BE=5﹣3=2,∠CDE=∠AED,
∵DE平分∠ADC,
∴∠CDE=∠ADE,
∴∠ADE=∠AED,
∴BC=AD=AE=2,
故选:B.
【点评】本题主要考查平行四边形的性质,平行线的性质,角平分线的定义,掌握平行四边形的性质是解题的关键.
4.已知直线y=kx+b,若k+b=﹣3,kb=2,则该直线不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据k+b=﹣3、kb=2得到k、b的符号,再根据图象与系数的关系确定直线经过的象限,进而求解即可.
解:∵k+b=﹣3,kb=2,
∴k<0,b<0,
∴直线y=kx+b经过二、三、四象限,即不经过第一象限.
故选:A.
【点评】本题考查了一次函数图象与系数的关系,解题的关键是根据k、b之间的关系确定其符号.
5.如图,在菱形ABCD中,点B在x轴上,点C的坐标为(6,2),点A的坐标为(0,2),则点D的坐标为( )
A.(4,4) B.(3,3) C.(3,4) D.(2,3)
【分析】连接AC、BD交于点E,由菱形的性质得出AC⊥BD,AE=CE=AC,BE=DE=BD,再由点C的坐标和点A的坐标得出OA=2,AC=6,则DE=2,AE=3,即可解决问题.
解:连接AC、BD交于点E,如图所示:
∵四边形ABCD是菱形,
∴AC⊥BD,AE=CE=AC,BE=DE=BD,
∵点C的坐标为(6,2),点A的坐标为(0,2),
∴OA=2,AC=6,
∴BE=DE=OA=2,AE=3,
∴BD=2DE=4,
∴点D的坐标为:(3,4),
故选:C.
【点评】本题考查了菱形的性质、坐标与图形性质;熟练掌握菱形的性质是解决问题的关键.
6.已知点(﹣1,a)和点(,b)都在直线y=2x﹣3的图象上,则a,b的大小关系是( )
A.a>b B.a<b
C.a=b D.a,b的大小不能确定
【分析】先根据一次函数的解析式判断出一次函数的增减性,再根据﹣1<即可得出结论.
解:∵一次函数y=2x﹣3中,k=2>0,
∴y随x的增大而增大,
∵﹣1<,
∴a<b.
故选:B.
【点评】本题考查的是一次函数图象上点的坐标特点,一次函数的性质,掌握一次函数的性质是解答此题的关键.
7.如图,菱形ABCD的边长为2,∠ADC=120°,点E为AB边的中点,点P是对角线AC上的一动点,则PB+PE的最小值为( )
A. B. C.2 D.3
【分析】找出B点关于AC的对称点D,连接DE交AC于P,则DE的长就是PB+PE的最小值,求出即可.
解:连接BD,交AC于O,连接DE交AC于P,
由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB,
∴PE+PB=PE+PD=DE,
即DE的长就是PE+PB的最小值.
∵四边形ABCD是菱形,∠ADC=120°,
∴∠DAB=60°,DA=AB=2,
∴△DAB是等边三角形,
∴DA=AB=DB=2,
∵点E为AB边的中点,
∴AE=BE=1,
∴DE⊥AB(等腰三角形三线合一的性质),
在Rt△ADE中,
DE===,
即PB+PE的最小值为.
故选:B.
【点评】本题主要考查轴对称﹣最短路线问题,菱形的性质,勾股定理等知识点,确定P点的位置是解答本题的关键.
8.如图,一次函数y=﹣x+b与反比例函数y=(x>0)的图象相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB,过点A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m,若S△OAF+S四边形EFBC=4,则m的值为( )
A.1 B. C.2 D.4
【分析】作AM⊥OD于M,BN⊥OC于N.记△AOF面积为S,则△OEF面积为2﹣S,四边形EFBC面积为4﹣S,△OBC和△OAD面积都是6﹣2S,△ADM面积为4﹣2S=2(2﹣S),所以S△ADM=2S△OEF,推出EF=AM=NB,得点B坐标(2m,)代入直线解析式即可解决问题.
解:作AM⊥OD于M,BN⊥OC于N.
∵一次函数y=﹣x+b与反比例函数y=(x>0)的图象都是关于直线y=x对称,
∴AD=BC,OD=OC,DM=AM=BN=CN,记△AOF面积为S,
则△OEF面积为2﹣S,四边形EFBC面积为4﹣S,△OBC和△OAD面积都是6﹣2S,△ADM面积为4﹣2S=2(2﹣S),
∴S△ADM=2S△OEF,
由对称性可知AD=BC,OD=OC,∠ODC=∠OCD=45°,△AOM≌△BON,AM=NB=DM=NC,
∴EF=AM=NB,
∴EF是△OBN的中位线,
∴N(2m,0),
∴点B坐标(2m,)代入直线y=﹣x+m+,
∴=﹣2m+m+,整理得到m2=2,
∵m>0,
∴m=.
故选:B.
【点评】本题考查反比例函数与一次函数图象的交点、对称等知识,解题的关键是利用对称性得到很多相等的线段,学会设参数解决问题.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
9.已知实数= 2022 .
【分析】根据二次根式有意义可得a的取值范围,再根据绝对值的性质解答即可.
解:由题意得,a﹣2022≥0,
解得a≥2022,
∵|2022﹣a|+=a,
∴a﹣2022+=a,
∴=2022,
即a﹣2022=20222,
∴a﹣20222=2022.
故答案为:2022.
【点评】本题考查的是二次根式有意义的条件以及实数的运算,掌握二次根式的被开方数是非负数是解题的关键.
10.如图是某旅行车旅客携带行李收费示意图,小李所携带的行李重20千克,那么小李应该交费 64 (元).
【分析】从图象可知是一次函数,设出函数式,由待定系数法即可求出函数式;把x=20代入可得.
解:设当x>5时,旅客携带行李收费的函数关系为 y=kx+b,
由图象过(5,4),(6,8)可得:
,
解得:,
∴y=4x﹣16.
将x=20代入可得:y=64,
故答案为:64.
【点评】本题考查了一次函数的应用,求出函数解析式是解决问题的关键.
11.如图,正方形ABCD的边长,AB=2点P为AB边上一点(不与小B重合),过点P、B在正方形内部作正方形PBEF,交边BC于点E,连结DF、CF,当△CDF为等腰三角形时,PB的长为 2﹣或1 .
【分析】分两种情形①当FD=CD=2时,②当FD=FC时,根据等腰直角三角形的性质求出AE即可解决问题.
解:连接BF,如图:
∵四边形ABCD、PBEF是正方形,AB=2,
∴B、F、D共线,CD=AB=2,
①当FD=CD=2时,BF=BD﹣FC=2﹣2,
∴PB=BF=2﹣;
②当FD=FC时,∠DFC=90°,∠FDC=∠FCD=45°,FD=CD=,
∴BF=BD﹣FD=2﹣=,
∴PB=BF=1.
∴当△CDE为等腰三角形时,PB=2﹣或1.
故答案为:2﹣或1.
【点评】本题考查正方形的性质、等腰三角形的定义,解题的关键是灵活运用等腰直角三角形的性质,记住等腰直角三角形的斜边等于直角边的倍,属于中考常考题型.
12.如图,一次函数y=﹣x+2的图象与x轴、y轴分别交于A、B两点,若点P(a+1,a﹣1)在△AOB的内部,则a的取值范围为 1<a< .
【分析】根据题意得出0<a+1<4,0<a﹣1<2,a﹣1<﹣(a+1)+2,解不等式组即可求得.
解:∵函数y=﹣x+2,
∴A(4,0),B(0,2),
∵点P在△AOB的内部,
∴0<a+1<4,0<a﹣1<2,a﹣1<﹣(a+1)+2,
∴1<a<.
故答案为:1<a<.
【点评】本题考查了一次函数图象上点的坐标特征,一次函数的性质,熟知图象上的点的坐标适合函数解析式是解题的关键.
三、计算题包含第13题4分、14题共2小题,每小题4分,共12分.
13.计算:35÷92+(﹣1)0.
【分析】直接利用幂的乘方运算法则将原式变形,再利用同底数幂的除法运算法则、零指数幂的性质化简,进而得出答案.
解:原式=35÷34+1
=3+1
=4.
【点评】此题主要考查了同底数幂的除法运算、零指数幂的性质等知识,正确化简各数是解题关键.
14.解方程:
①2x2﹣5x﹣3=0;
②.
【分析】(1)利用因式分解法求解即可;
(2)方程两边都乘以最简公分母(x+1(x﹣1),把分式方程化为整式方程,然后求解即可,最后进行检验.
解:①2x2﹣5x﹣3=0;
(2x+1)(x﹣3)=0,
∴2x+1=0,x﹣3=0,
解得x1=﹣,x2=3;
②.
方程两边都乘以(x+1(x﹣1)得,
2+(x+1(x﹣1)=x(x+1)
解得x=1,
检验:当x=1时,(x+1(x﹣1)=0,
∴x=1是分式方程的增根,
故原分式方程的无解.
【点评】本题主要考查了因式分解法求一元二次方程,解分式方程,注意解分式方程要检验,解一元二次方程要根据方程的特点灵活选用合适的方法.
四、简答题包含第15题、16题、17题,共3小题,每小题8分,共24分.
15.化简:÷(1﹣)2.
【分析】先进行通分,把除法转为乘法,再约分即可.
解:÷(1﹣)2
=
=
=x2(x+1)
=x3+x2.
【点评】本题主要考查分式的混合运算,解答的关键是对相应的运算法则的掌握.
16.如图,在▱ABCD中,点E为边CD的中点,连结BE并延长交AD的延长线于点F,连结CF.
求证:四边形BCFD为平行四边形.
【分析】证△BCE≌△FDE(AAS),得BE=FE,再由平行四边形的判定定理即可得出结论.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠FDE=∠BCE,
∵点E是CD的中点,
∴CE=DE,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(AAS),
∴BE=FE,
又∵CE=DE,
∴四边形BCFD为平行四边形.
【点评】本题考查平行四边形的判定与性质、全等三角形的判定与性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
17.如图,点A、B分别在反比例函数和的图象上,线段AB与x轴相交于点P.
(1)如图①,若AB⊥x轴,且|AP|=2|PB|,k1+k2=1.求k1、k2的值;
(2)如图②,若点P是线段AB的中点,且△OAB的面积为2.求k1﹣k2的值.
【分析】(1)连接OA、OB,根据反比例函数系数k的几何意义以及|AP|=2|PB|得到S△AOP=2S△BOP,即k1+2k2=0①,由k1+k2=1②.①﹣②得,k2=﹣1,进而求得k1=2;
(2)作AM⊥x轴于M,BN⊥x轴于N,则S△AOM=k1,S△BON=﹣k2,根据题意得到S△AOP=S△BOP=1,S△APM=S△BPN,即可得到k1﹣1=1﹣(﹣k2),整理得k1﹣k2=4.
解:(1)如图1,连接OA、OB,
∵AB⊥x轴,
∴S△AOP=k1,S△BOP=﹣k2,
∵|AP|=2|PB|,
∴S△AOP=2S△BOP,即k1=2×(﹣k2),
∴k1+2k2=0①,
∵k1+k2=1②.
①﹣②得,k2=﹣1,
∴k1=2;
(2)如图2,作AM⊥x轴于M,BN⊥x轴于N,则S△AOM=k1,S△BON=﹣k2,
∵点P是线段AB的中点,且△OAB的面积为2,
∴S△AOP=S△BOP=1,
在△APM和△BPN中,
,
∴△APM≌△BPN(AAS),
∴S△APM=S△BPN,
∴k1﹣1=1﹣(﹣k2),
整理得k1﹣k2=4.
【点评】本题考查了反比例函数系数k的几何意义,反比例函数的性质,正确作出辅助线是解题的关键.
五、解答题共2小题,第18题12分,第19题12分,共24分.
18.点P为正方形ABCD对角线BD上的一个动点,作射线AP,BF⊥AP于F,DE⊥AP于E,点O为BD中点.
(1)如图1,点P在DO上时,求证:△ADE≌△BAF;
(2)如图2,作射线EO,交BF所在直线于点G,求证:B,G,D,E四点所围成的四边形是平行四边形;
(3)在(2)的条件下,若AB=13,AF=12,求平行四边形BGDE的面积.
【分析】(1)根据等角的余角相等得∠DAE=∠ABF,利用AAS即可得出结论;
(2)证明△EDO≌△GBO(ASA),根据全等三角形的性质得EO=GO,由DO=BO,EO=GO即可得出结论;
(3)根据勾股定理求出BF=5,由(1)知△ADE≌△BAF,根据全等三角形的性质得DE=AF=12,BF=AE=5,利用线段的和差求出EF=12﹣5=7,即可得平行四边形BGDE的面积.
【解答】(1)证明:∵四边形ABCD是正方形,BF⊥AP,DE⊥AP,
∴DA=AB,∠DEA=∠AFB=∠DAB=90°,
∴∠DAE+∠FAB=∠ABF+∠FAB=90°,
∴∠DAE=∠ABF,
在△ADE和△BAF中,
,
∴△ADE≌△BAF(AAS);
(2)证明:∵BF⊥AP,DE⊥AP,
∴BG∥DE.
∴∠EDO=∠GBO,
∵点O为BD中点.
∴DO=BO.
在△EDO△GBO中,
,
∴△EDO≌△GBO(ASA),
∴EO=GO,
∵DO=BO,EO=GO,
∴四边形BGDE是平行四边形;
(3)解:如图:
∵AB=13,AF=12,BF⊥AP,
∴BF==5,
由(1)知△ADE≌△BAF,
∴DE=AF=12,BF=AE=5,
∴EF=AF﹣AE=12﹣5=7,
∴平行四边形BGDE的面积为DE•EF=12×7=84.
【点评】本题是四边形综合题,考查了正方形的性质,全等三角形的判定和性质,平行四边形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形解决问题.
19.如图,已知点A(t,1)在第一象限,将OA绕点O顺时针旋转45°得到OB,若反比例数y=(k>0)的图象经过点A、B,求k的值.
【分析】根据反比例函数图象关于直线y=x的对称性得,B(1,t),过点A作AC⊥y轴于点C,BE⊥x轴于点E,又由k的几何意义可得k=t,作AO的垂直平分线DE,可得∠CDA=45°,连接AD,根据OC=OD+DC,即1=t+t,进而求出t的值,即为k的值.
解:如图,点A(t,1),将OA绕点O顺时针旋转45°得到OB,
根据反比例函数图象关于直线y=x的对称性得,
B(1,t),
过点A作AC⊥y轴于点C,BE⊥x轴于点E,
又由k的几何意义可知:
k=1×t=t,
∵∠AOB=45°,
∴∠AOC=∠BOE=22.5°,
∴tan∠AOC=tan22.5°==t=k,
作AO的垂直平分线DF,连接AD,
∴AD=OD,
∴∠DAO=∠DOA=22.5°,
∴∠CDA=45°,
∴DC=CA=t,
∴AD=DO=t,
∴OC=OD+DC,
即1=t+t,
解得t=﹣1.
所以k=﹣1.
【点评】本题考查了反比例函数系数k的几何意义、旋转的性质,解决本题的关键是掌握反比例函数的性质.
2023-2024学年四川省眉山市东坡实验中学八年级(上)期中数学试卷(含解析): 这是一份2023-2024学年四川省眉山市东坡实验中学八年级(上)期中数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
四川省眉山市东坡区眉山北外附属东坡外国语学校2022-2023学年七年级下学期开学考试数学试题答案: 这是一份四川省眉山市东坡区眉山北外附属东坡外国语学校2022-2023学年七年级下学期开学考试数学试题答案,共17页。试卷主要包含了凡作图题或辅助线均用签字笔画图等内容,欢迎下载使用。
四川省眉山市东坡区眉山北外附属东坡外国语学校2022-2023学年七年级下学期开学考试数学试题: 这是一份四川省眉山市东坡区眉山北外附属东坡外国语学校2022-2023学年七年级下学期开学考试数学试题,共6页。试卷主要包含了凡作图题或辅助线均用签字笔画图等内容,欢迎下载使用。












