九年级上册数学第22章 二次函数专题08 二次函数与PA-PB最大值

这是一份九年级上册数学第22章 二次函数专题08 二次函数与PA-PB最大值，文件包含专题08二次函数与PA-PB最大值原卷版docx、专题08二次函数与PA-PB最大值解析版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。
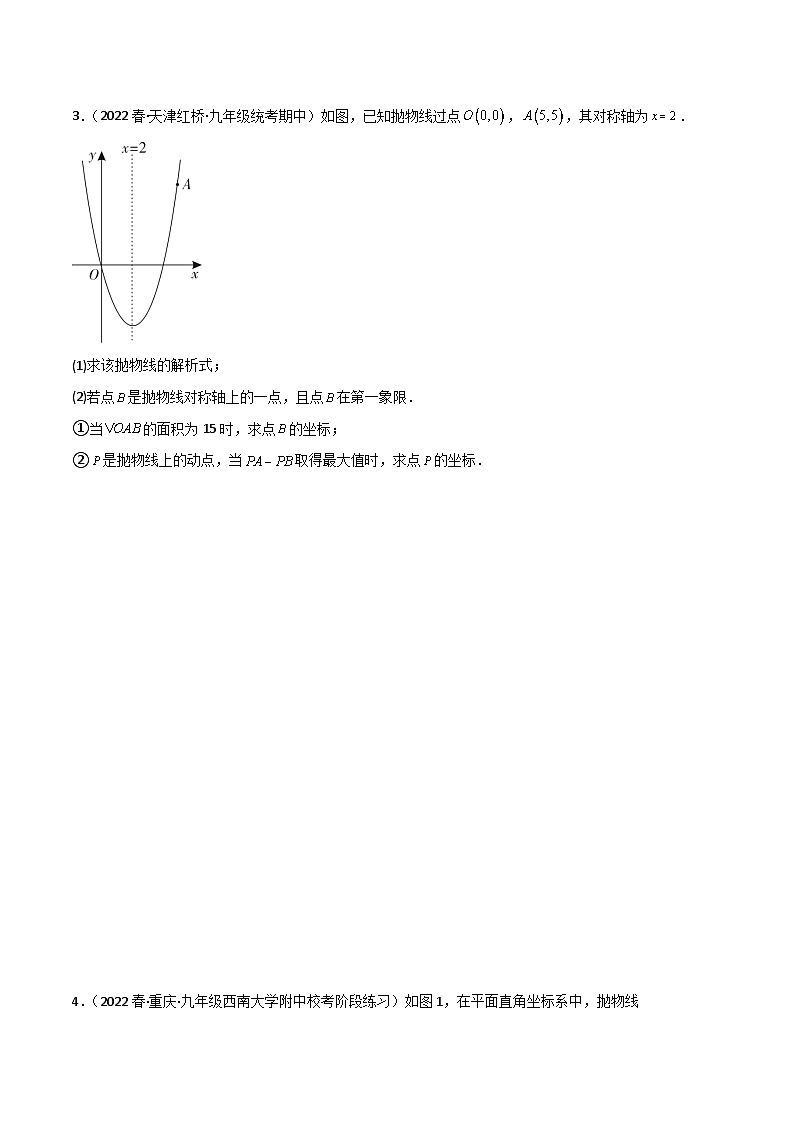
专题08 二次函数与PA-PB最大值解题点拨1．口诀：同侧差最大 2．图形：如图 1 所示，A、B 为定点，P 为 l 上一动点，试求 的最大值与最小值． 解析 1：“最大值” ①     两边只差小于第三边， ≤AB，当 A、B、P 三点共线时，取等号 ② 所以连接 BA 并延长与 l 的交点即为所求点解析 2：“最小值” ① 绝对值具有非负性 ≥0，当 AP＝PB 时成立 ② P 为 AB 中垂线与 l 的交点．直击中考1．（2022·湖南常德·统考中考真题）如图，已经抛物线经过点，，且它的对称轴为．(1)求此抛物线的解析式；(2)若点是抛物线对称轴上的一点，且点在第一象限，当的面积为15时，求的坐标；(3)在（2）的条件下，是抛物线上的动点，当的值最大时，求的坐标以及的最大值       2．（2022春·山东临沂·九年级统考期中）如图，已知抛物线过点，，且它的对称轴为，点是抛物线对称轴上的一点，且点在第一象限．(1)求此抛物线的解析式；(2)当的面积为时，求的坐标；(3)在（2）的条件下，是抛物线上的动点，当的值最大时，求的坐标以及的最大值．        3．（2022春·天津红桥·九年级统考期中）如图，已知抛物线过点，，其对称轴为．(1)求该抛物线的解析式；(2)若点是抛物线对称轴上的一点，且点在第一象限．①当的面积为15时，求点的坐标；②是抛物线上的动点，当取得最大值时，求点的坐标．                4．（2022春·重庆·九年级西南大学附中校考阶段练习）如图1，在平面直角坐标系中，抛物线与x轴交于点B，与y轴交于点C，其对称轴是直线．(1)求抛物线解析式；(2)如图2，P是直线BC下方抛物线上一动点，连接PC、PB，当四边形ACPB面积最大时，y轴上有一点Q，使得的值最大，求出的最大值与此时的Q点坐标；(3)如图3，抛物线上有一点，在（2）的条件下，将抛物线沿射线AP平移2个单位长度得到新抛物线，点D是新抛物线上一点，点F在直线CP上，是否存在以点A，D，E，F为顶点的平行四边形？若存在，请直接写出点D的横坐标，若不存在，请说明理由，             5．（2022春·四川眉山·九年级校考期末）如图，已知抛物线与直线y=0.5x＋3相交于A，B两点，交ⅹ轴于C，D两点，连接AC，BC，已知A（0，3），C（－3，0）.(1)求抛物线的表达式；(2)在抛物线对称轴l上找一点M，使|MB一MD|的值最大，并求出这个最大值；(3)点P为y轴右侧抛物线上的一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，是否存在点P，使得以A，P，Q为顶点的三角形与△ABC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由.                6．（2022秋·九年级单元测试）如图，已知抛物线的解析式为，抛物线与x轴交于点A和点B，与y轴交点于点C．(1)请分别求出点A、B、C的坐标和抛物线的对称轴；(2)连接AC、BC，将△ABC绕点B顺时针旋转90°，点A、C的对应点分别为M、N，求点M、N的坐标；(3)若点为该抛物线上一动点，在（2）的条件下，请求出使最大时点的坐标，并请直接写出的最大值．               7．（贵州省安顺市2019年中考数学试题）如图，抛物线与直线分别相交于，两点，且此抛物线与轴的一个交点为，连接，．已知，．（1）求抛物线的解析式；（2）在抛物线对称轴上找一点，使的值最大，并求出这个最大值；（3）点为轴右侧抛物线上一动点，连接，过点作交轴于点，问：是否存在点使得以，，为顶点的三角形与相似？若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．               8．（2022·广东汕头·统考一模）已知二次函数．(1)对于任意m，二次函数都会经过一个定点，求此定点的坐标；(2)当时，如图，二次函数与y轴的交点为M，顶点为N．①若点P是x轴上的动点，求的最大值及对应的点P的坐标；②设点Q是二次函数上的动点，点H是直线MN上的动点，是否存在点Q，使得△OQH是以点Q为直角顶点的等腰Rt△OQH？若存在，求出点Q的坐标；若不存在，请说明理由．