九年级上册数学第22章 二次函数专题14 二次函数与菱形存在性问题

这是一份九年级上册数学第22章 二次函数专题14 二次函数与菱形存在性问题，文件包含专题14二次函数与菱形存在性问题原卷版docx、专题14二次函数与菱形存在性问题解析版docx等2份试卷配套教学资源，其中试卷共60页， 欢迎下载使用。
专题14 二次函数与菱形存在性问题
解题点拨
【基本概念】
菱形作为一种特殊的平行四边形，可以从以下几种方式得到：
（1）有一组邻边相等的平行四边形菱形；
（2）对角线互相垂直的平行四边形是菱形；
（3）四边都相等的四边形是菱形．
【解题技巧】
坐标系中的菱形存在性问题也是依据以上去得到方法．和平行四边形相比，菱形多一个“对角线互相垂直”或“邻边相等”，但这两者其实是等价的，故若四边形ABCD是菱形，则其4个点坐标需满足：

考虑到互相垂直的两条直线斜率之积为1在初中并不适合直接用，故取两邻边相等．
即根据菱形的图形性质，我们可以列出关于点坐标的3个等式，
故菱形存在性问题点坐标最多可以有3个未知量，与矩形相同．
【基本题型】
因此就常规题型而言，菱形存在性至少有2个动点，多则有3个动点，可细分如下两大类题型：
（1）2个定点+1个半动点+1个全动点
（2）1个定点+3个半动点
【解题思路】
解决问题的方法也可有如下两种：
思路1：先平四，再菱形
设点坐标，根据平四存在性要求列出“A+C=B+D”（AC、BD为对角线），再结合一组邻边相等，得到方程组．

思路2：先等腰，再菱形
在构成菱形的4个点中任取3个点，必构成等腰三角形，根据等腰存在性方法可先确定第3个点，再确定第4个点．


【例题解析】
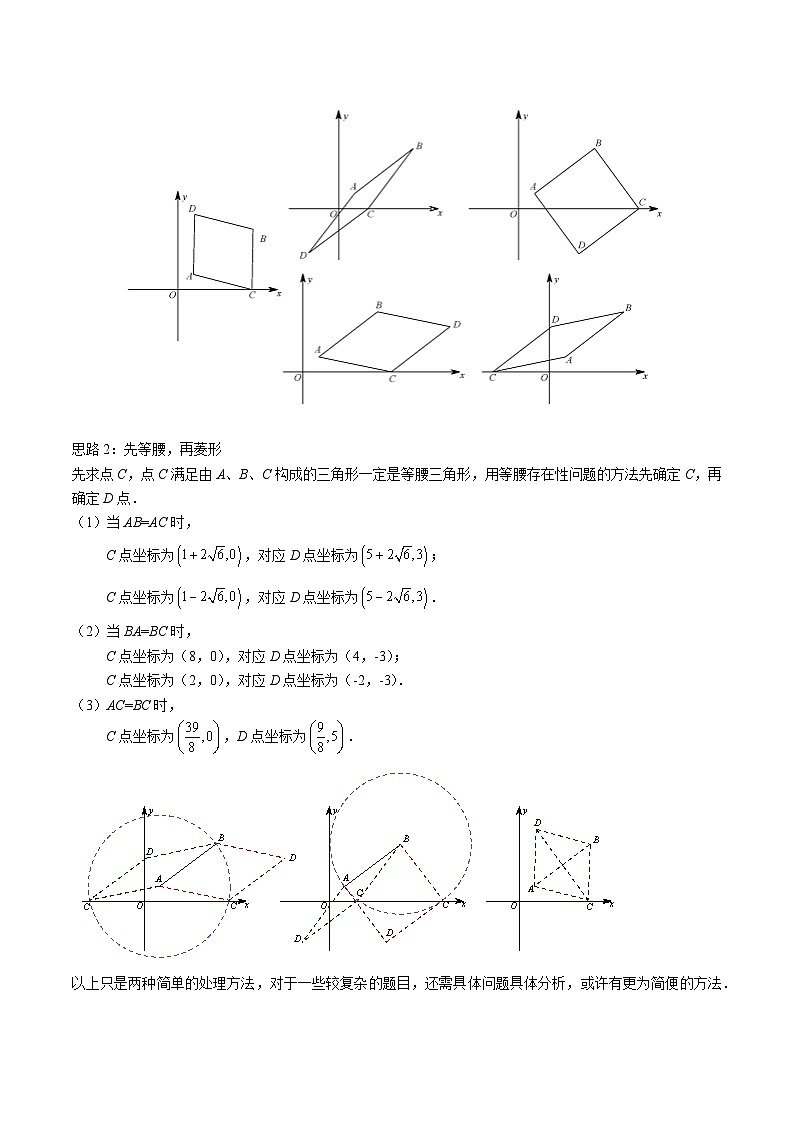
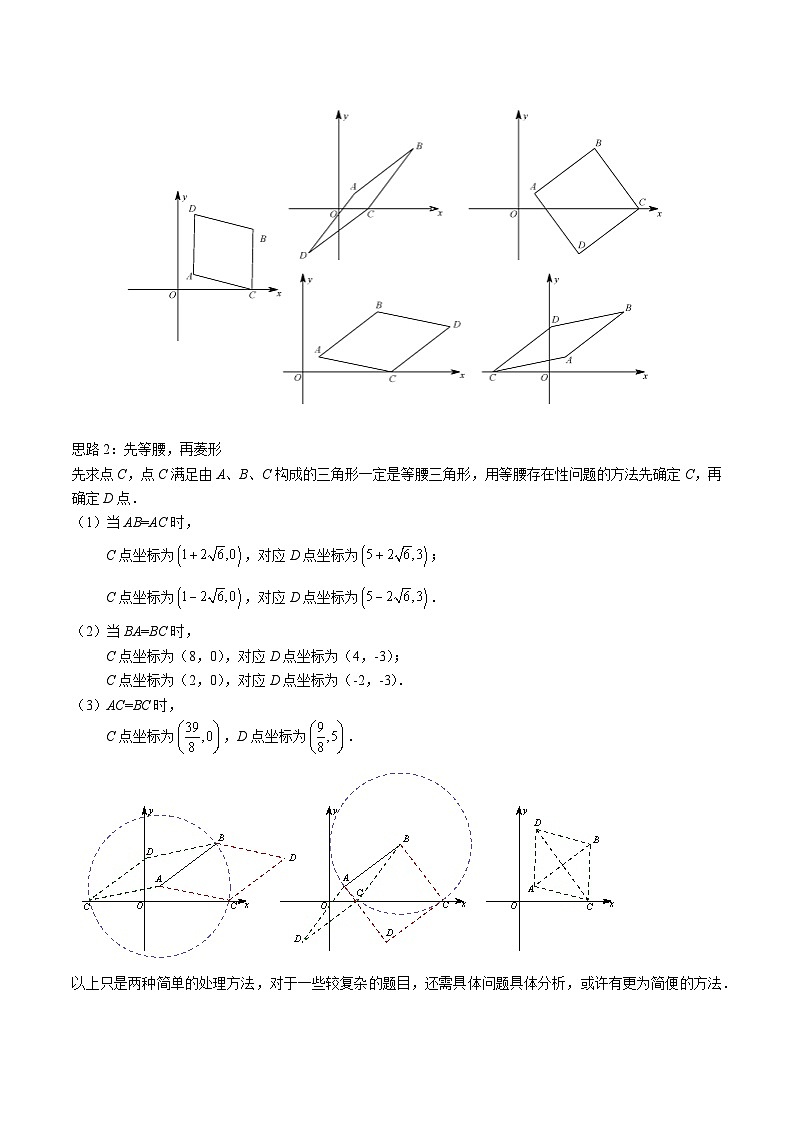
如图，在坐标系中，A点坐标（1,1），B点坐标为（5,4），点C在x轴上，点D在平面中，求D点坐标，使得以A、B、C、D为顶点的四边形是菱形．



思路1：先平四，再菱形
设C点坐标为（m，0），D点坐标为（p，q）．
（1）当AB为对角线时，由题意得：（AB和CD互相平分及AC=BC）
，解得：
（2）当AC为对角线时，由题意得：（AC和BD互相平分及BA=BC）
，解得：或
（3）当AD为对角线时，由题意得：
，解得：或



思路2：先等腰，再菱形
先求点C，点C满足由A、B、C构成的三角形一定是等腰三角形，用等腰存在性问题的方法先确定C，再确定D点．
（1）当AB=AC时，
C点坐标为，对应D点坐标为；
C点坐标为，对应D点坐标为．
（2）当BA=BC时，
C点坐标为（8，0），对应D点坐标为（4，-3）；
C点坐标为（2，0），对应D点坐标为（-2，-3）．
（3）AC=BC时，
C点坐标为，D点坐标为．

以上只是两种简单的处理方法，对于一些较复杂的题目，还需具体问题具体分析，或许有更为简便的方法．

直击中考
1．（四川德阳模拟预测）如图，在平面直角坐标系中，抛物线与轴分别交于点和点，与轴交于点，连接．

(1)求抛物线的解析式及点的坐标；
(2)如图，点为线段上的一个动点（点不与点，重合），过点作轴的平行线交抛物线于点，求线段长度的最大值．
(3)动点以每秒个单位长度的速度在线段上由点向点运动，同时动点以每秒个单位长度的速度在线段上由点向点运动，在平面内是否存在点，使得以点，，，为顶点的四边形是菱形？若存在，请直接写出符合条件的点的坐标；若不存在，请说明理由．
【答案】(1)，
(2)当时，
(3)存在，或或

【分析】（1）利用待定系数法求出抛物线解析式，再令，可得，求解即可得点的坐标；
（2）由两点坐标求出直线的解析式，进而设出点的坐标，进而得出结论；
（3）要使点，，，为顶点的四边形是菱形，只需为等腰三角形，所以，或，结合图形得到答案即可．
【详解】（1）解：由题意，将点、代入，
可得 ，解得，
∴，
当时，可有 ，
解得，，
∴；
（2）设直线的解析式为 ，将点、代入，
可得，解得，
∴，
设点，，
∴，
∴当时，有；
（3）如图1，

∵，，
∴，
∴，
作轴于，
∴，
当时，
∴，
∵，
∴四边形为矩形，
∴，
由得，
∴，
∴，
∴，
∴；
如图，

当时，作轴于，作轴于，
∴，
可得四边形是矩形，
∴，
∴，
∴，
∴，
∴，
∴；
如图，

当时，
，
∴，
∴，
∴．
综上所述：或或．
【点睛】本题主要考查了二次函数的图像与性质、待定系数法求一次函数和二次函数解析式、等腰三角形的性质和菱形的性质等知识，解题关键是熟练掌握先关知识，运用分类讨论和数形结合的思想分析问题，并画出符合条件的图形．
2．如图，在平面直角坐标系中，抛物线与直线交于A，B两点，其中，．

(1)求该抛物线的函数表达式；
(2)点P，Q为直线下方抛物线上任意两点，且满足点P的横坐标为m，点Q的横坐标为，过点P和点Q分别作y轴的平行线交直线于C点和D点，连接，求四边形面积的最大值；
(3)在（2）的条件下，将抛物线沿射线平移2个单位，得到新的抛物线，点E为点P的对应点，点F为的对称轴上任意一点，点G为平面直角坐标系内一点，当点构成以为边的菱形时，直接写出所有符合条件的点G的坐标．
【答案】(1)；
(2)；
(3)、、．

【分析】（1）用待定系数法求解即可；
（2）根据题意，求得直线解析式，以及四点坐标，得到、长度，利用二次函数的性质求解即可；
（3）根据平移的性质，求得的表达式，分两种情况，讨论求解即可．
【详解】（1）解：将，代入二次函数解析式，可得
，解得
即；
（2）设直线解析式，代入，，可得
，解得
即，
则，，，
，
，
，
即当时，最大，为；
（3）由（2）可知，
直线为与轴的交点为，与轴的交点为，两点之间的距离为，
沿射线平移个单位，可看成向右移动了4个单位，向下移动了2个单位，
∴，
则平移后，
抛物线的对称轴为，
设，
当时，如图：

则，
解得，
∴或，
当时，平移到，平移到，
∴，
当时，平移到，平移到，
∴，
当时，如下图：

，解得，
平移到，平移到，可得，
综上点的坐标为、、．
【点睛】本题考查二次函数综合应用，涉及待定系数法，四边形面积、菱形的性质及应用等知识解题的关键是用含字母的代数式表示相关点坐标和相关线段的长度．
3．（2022·山东烟台·统考中考真题）如图，已知直线y＝x+4与x轴交于点A，与y轴交于点C，抛物线y＝ax2+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝﹣1．

(1)求抛物线的表达式；
(2)D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；
(3)若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．
【答案】(1)y＝﹣x2﹣x+4
(2)S最大＝，D（﹣，5）
(3)存在，Q（﹣2，）

【分析】（1）先求得A，C，B三点的坐标，将抛物线设为交点式，进一步求得结果；
（2）作DF⊥AB于F，交AC于E，根据点D和点E坐标可表示出DE的长，进而表示出三角形ADC的面积，进而表示出S的函数关系式，进一步求得结果；
（3）根据菱形性质可得PA＝PC，进而求得点P的坐标，根据菱形性质，进一步求得点Q坐标．
【详解】（1）解：当x＝0时，y＝4，
∴C （0，4），
当y＝0时，x+4＝0，
∴x＝﹣3，
∴A （﹣3，0），
∵对称轴为直线x＝﹣1，
∴B（1，0），
∴设抛物线的表达式：y＝a（x﹣1）•（x+3），
∴4＝﹣3a，
∴a＝﹣，
∴抛物线的表达式为：y＝﹣（x﹣1）•（x+3）＝﹣x2﹣x+4；
（2）如图1，

作DF⊥AB于F，交AC于E，
∴D（m，﹣﹣m+4），E（m，﹣m+4），
∴DE＝﹣﹣m+4﹣（m+4）＝﹣m2﹣4m，
∴S△ADC＝OA＝•（﹣m2﹣4m）＝﹣2m2﹣6m，
∵S△ABC＝＝＝8，
∴S＝﹣2m2﹣6m+8＝﹣2（m+）2+，
∴当m＝﹣时，S最大＝，
当m＝﹣时，y＝﹣＝5，
∴D（﹣，5）；
（3）设P（﹣1，n），
∵以A，C，P，Q为顶点的四边形是以AC为对角线的菱形，
∴PA＝PC，
即：PA2＝PC2，
∴（﹣1+3）2+n2＝1+（n﹣4）2，
∴n＝，
∴P（﹣1，），
∵xP+xQ＝xA+xC，yP+yQ＝yA+yC
∴xQ＝﹣3﹣（﹣1）＝﹣2，yQ＝4﹣＝，
∴Q（﹣2，）．
【点睛】本题考查了二次函数及其图象性质，勾股定理，菱形性质等知识，解决问题的关键是熟练掌握相关二次函数和菱形性质
4．（2021·内蒙古鄂尔多斯·统考中考真题）如图，抛物线与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．

（1）求A，B，C三点的坐标；
（2）连接，直线与该抛物线交于点E，与交于点D，连接．当时，求线段的长；
（3）点M在y轴上，点N在直线上，点P为抛物线对称轴上一点，是否存在点M，使得以C、M、N、P为顶点的四边形是菱形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
【答案】（1）A（-4,0），B（2,0），C（0，-8）；（2）；（3）存在，M、、
【分析】（1）分别令x=0、y=0即可求出A，B，C三点的坐标；
（2）先求出AC解析式，用m表示出DE坐标，最后根据求出m的值即可；
（3）分三种情况：对角线或为对角线或为对角线，①当为对角线时，，，可得出，根据，即可求出答案；②当为对角线时，，，设，则，，建立方程求解即可；③当对角线时，与互相垂直平分，设，则，，根据在直线上，即可求得答案．
【详解】解：（1）令x=0得，
∴C点坐标（0，-8）
令y=0得：，
解得：，
∴A（-4,0），B（2,0）；
（2）设DE交x轴于F，

设AC解析式为，代入AC坐标得：
，
解得
∴AC解析式为，
∵直线与该抛物线交于点E，与交于点D，
∴，
∴，
∵，
∴，
∴，
∴，
∴，
解得，
∴；
（3）存在，
如图2，，
抛物线对称轴为直线，
以、、、为顶点的四边形是菱形，
分三种情况：对角线或为对角线或为对角线，
①当为对角线时，，，
点为直线与抛物线对称轴的交点，即，
，
，
，；
②当为对角线时，，，
设，则，，
，
解得：，
，
③当对角线时，与互相垂直平分，设，则，，
在直线上，
，
，
综上所述，点的坐标为：，，，．

【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质和菱形的性质；会利用相似三角形处理垂直．
5．（2021·湖南娄底·统考中考真题）如图，在直角坐标系中，二次函数的图象与x轴相交于点和点，与y轴交于点C．

（1）求的值；
（2）点为抛物线上的动点，过P作x轴的垂线交直线于点Q．
①当时，求当P点到直线的距离最大时m的值；
②是否存在m，使得以点为顶点的四边形是菱形，若不存在，请说明理由；若存在，请求出m的值．
【答案】（1）b=，c=；（2）①；②不存在，理由见解析
【分析】（1）将A（-1，0），B（3，0）代入y=x2+bx+c，可求出答案；
（2）①设点P（m，m2-2m-3），则点Q（m，m），再利用二次函数的性质即可求解；
②分情况讨论，利用菱形的性质即可得出结论．
【详解】解：（1）∵抛物线y=-x2+bx+c与x轴交于点A（-1，0），B（3，0），
∴，
解得：，
∴b=，c=；
（2）①由（1）得，抛物线的函数表达式为：y=x2，
设点P（m，m2-2m-3），则点Q（m，m），
∵0