数学九年级上册5 三角函数的应用教案及反思

这是一份数学九年级上册5 三角函数的应用教案及反思，共4页。教案主要包含了自学提纲，典例解析，对应练习，学习小结等内容，欢迎下载使用。
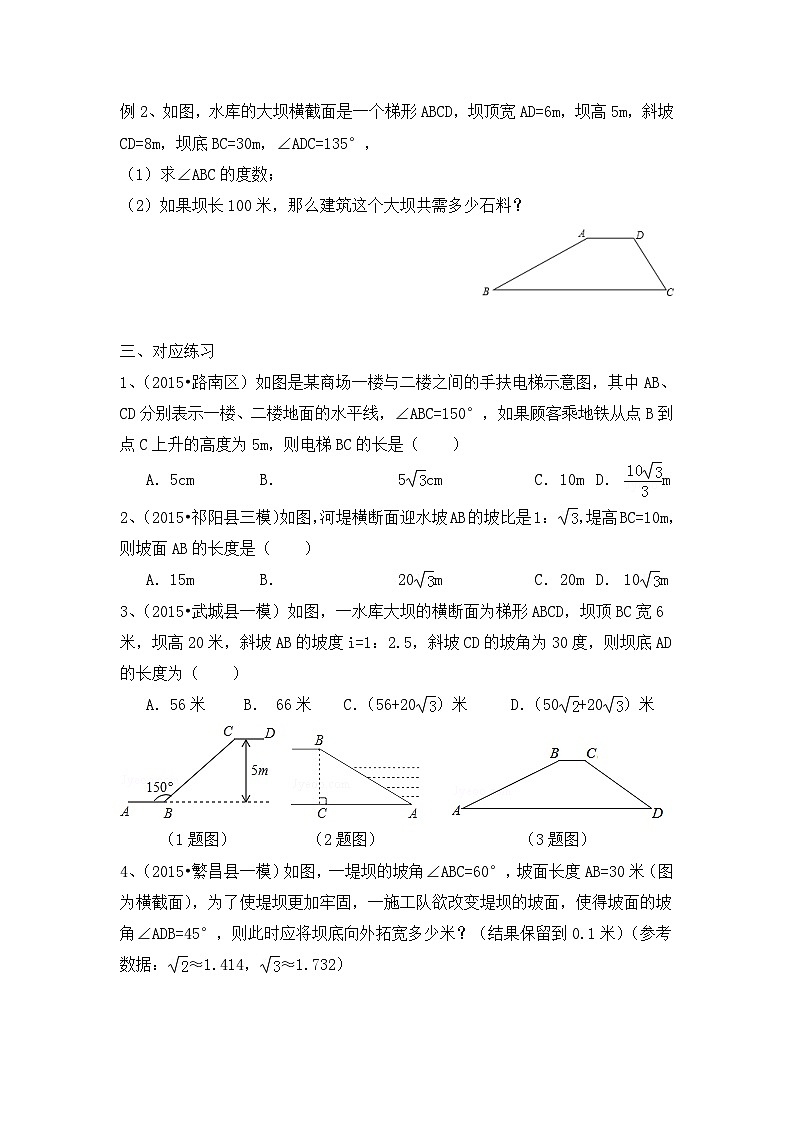
2.5三角函数的应用（第2课时）学习目标1、使学生理解坡角、坡比等概念的意义，并能解决有关实际问题；2、使学生能适当的选择锐角三角函数关系式去解决直角三角形问题.学习重难点1、用三角函数有关知识解决方位角和坡角、坡比的实际问题；2、学会准确分析问题并将实际问题转化成数学模型。学习过程一、自学提纲1、 坡面的                 的比叫做坡度（或叫做坡比），2、一般用i表示。即ｉ＝（ ）常写成i=1：m的形式，如i=1:2.5把坡面与水平面的夹角α叫做坡角． 结合图形思考，坡度i与坡角α之间具有什么关系？               3、即学即用：(1)一段坡面的坡角为60°，则坡度i=______；（2）已知一段坡面上，铅直高度为，坡面长为，则坡度i=        ，坡角α   度。二、典例解析例1，如图，水库大坝的横截面是梯形，坝顶宽6m，坝高23m，斜坡AB的坡度i=1:3, 斜坡CD的坡度i=1:2.5，求斜坡AB的坡角a，坝底宽AD 和斜坡AB的长（精确到0.1米）分析：将实际问题转化为数学问题，应用坡度、坡角的概念及联系，即i＝tanα＝          ，将梯形问题，添加高线把梯形转化为            来解.    例2、如图，水库的大坝横截面是一个梯形ABCD，坝顶宽AD=6m，坝高5m，斜坡CD=8m，坝底BC=30m，∠ADC=135°，（1）求∠ABC的度数；（2）如果坝长100米，那么建筑这个大坝共需多少石料？ 三、对应练习1、（2015•路南区）如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，如果顾客乘地铁从点B到点C上升的高度为5m，则电梯BC的长是（　　）　 A．5cm B． 5cm C． 10m D． m2、（2015•祁阳县三模）如图，河堤横断面迎水坡AB的坡比是1：，堤高BC=10m，则坡面AB的长度是（　　）　 A．15m B． 20m C． 20m D． 10m3、（2015•武城县一模）如图，一水库大坝的横断面为梯形ABCD，坝顶BC宽6米，坝高20米，斜坡AB的坡度i=1：2.5，斜坡CD的坡角为30度，则坝底AD的长度为（　　）　 A．56米 B． 66米    C．（56+20）米 D．（50+20）米           （1题图）         （2题图）                 （3题图）4、（2015•繁昌县一模）如图，一堤坝的坡角∠ABC=60°，坡面长度AB=30米（图为横截面），为了使堤坝更加牢固，一施工队欲改变堤坝的坡面，使得坡面的坡角∠ADB=45°，则此时应将坝底向外拓宽多少米？（结果保留到0.1米）（参考数据：≈1.414，≈1.732） 5、　（2015•黔南州）如图是一座人行天桥的示意图，天桥的高度是10米，CB⊥DB，坡面AC的倾斜角为45°．为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面DC的坡度为i=：3．若新坡角下需留3米宽的人行道，问离原坡角（A点处）10米的建筑物是否需要拆除？（参考数据：≈1.414，≈1.732）      四、学习小结         
参考答案1、C．2、C．3、C．4、解：过A点作AE⊥CD于E．在Rt△ABE中，∵∠ABE=60°．∴AE=AB•sin60°=30×=15（米），BE=AB•cos60°=30×=15（米），在Rt△ADE中，∵∠ADB=45°，∴DE=AE=15（米），∴DB=DE﹣BE=15﹣15≈11.0（米）．故此时应将坝底向外拓宽大约11.0米．          （4题图）             （8题图）5、解：需要拆除，理由为：∵CB⊥AB，∠CAB=45°，∴△ABC为等腰直角三角形，∴AB=BC=10米，在Rt△BCD中，新坡面DC的坡度为i=：3，即∠CDB=30°，∴DC=2BC=20米，BD==10米，∴AD=BD﹣AB=（10﹣10）米≈7.32米，∵3+7.32=10.32＞10，∴需要拆除